山东省青岛市市北区2022年九年级下学期数学中考二模试题

试卷更新日期：2022-05-31 类型：中考模拟

进入出卷网下载

一、单选题

1. 如图，在数轴上若两个不同的点A和B到原点的距离相等，则点B所表示的数是（）

A、3 B、 $\pm 3$ C、－3 D、 $\frac{1}{3}$

查看试题解析
2. 下列漂亮的图案中似乎包含了一些曲线，其实它们这种神韵是由多条线段呈现出来的，这些图案中既是中心对称图形又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 2021年5月15日07时18分，我国首个火星探测器“天问一号”经过470000000公里旅程成功着陆在火星上，从此，火星上留下中国的脚印，同时也为我国的宇宙探测之路迈出重要一步.将470000000用科学记数法表示为（）

A、 $47 \times 10^{7}$ B、 $4.7 \times 10^{7}$ C、 $4.7 \times 10^{8}$ D、 $0.47 \times 10^{9}$

查看试题解析
4. 如图，小明从 $A$ 入口进入博物馆参观，参观后可从 $B$ ， $C$ ， $D$ 三个出口走出，他恰好从 $C$ 出口走出的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

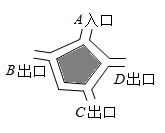查看试题解析
5. 如图所示的领奖台是由三个长方体组合而成的几何体，则这个几何体的左视图是（）

A、 B、 C、 D、

查看试题解析
6. 如图，在平面直角坐标系中，△ABC位于第二象限，点A的坐标是 $(- 2 ， 3)$ ，先将△ABC绕点 $(- 1 ， 0)$ 顺时针旋转90度得到 $△ A_{1} B_{1} C_{1}$ ，再以原点为位似中心作 $△ A_{1} B_{1} C_{1}$ 的位似图形 $△ A_{2} B_{2} C_{2}$ ，若 $△ A_{1} B_{1} C_{1}$ 与 $△ A_{2} B_{2} C_{2}$ 的相似比为1∶2，则点A的对应点 $A_{2}$ 的坐标是（）

A、 $(4 ， 2)$ B、 $(6 ， 4)$ C、 $(6 ， 4)$ 或 $(- 6 ， - 4)$ D、 $(4 ， 2)$ 或 $(- 4 ， - 2)$

查看试题解析
7. 如图，矩形纸片 $A B C D$ ， $A D ： A B = \sqrt{2} ： 1$ ，点 $E$ ， $F$ 分别在 $A D$ ， $B C$ 上，把纸片如图沿 $E F$ 折叠，点 $A$ ， $B$ 的对应点分别为 $A^{'}$ ， $B^{'}$ ，连接 $A A^{'}$ 并延长交线段 $C D$ 于点 $G$ ，则 $\frac{E F}{A G}$ 的值为（）

A、 $\frac{\sqrt{2}}{2}$ B、 $\frac{2}{3}$ C、 $\frac{1}{2}$ D、 $\frac{\sqrt{5}}{3}$

查看试题解析
8. 如图，二次函数y＝ax²+bx的图象经过点P ，若点P的横坐标为﹣1，则一次函数y＝（a﹣b）x+b的图象大致是（　　）

A、 B、 C、 D、

查看试题解析

二、填空题

9. 分解因式： $5 x^{2} - 5 y^{2} =$ ．

查看试题解析
10. 为了庆祝中国共产党成立100周年，某校举行“党在我心中”演讲比赛，评委将从演讲内容，演讲能力，演讲效果三个方面给选手打分，各项成绩均按百分制计，然后再按演讲内容占50%，演讲能力占40%，演讲效果占10%，计算选手的综合成绩（百分制）.小婷的三项成绩依次是84，95，90，她的综合成绩是.

查看试题解析
11. 《九章算术》是人类科学史上应用数学的“算经之首”，书中记载：今有三人共车，二车空；二人共车，九人步．问：人与车各几何？译文：若3人坐一辆车，则两辆车是空的；若2人坐一辆车，则9人需要步行，问：人与车各多少？设有x辆车，人数为y，根据题意可列方程组为．

查看试题解析
12. 如图，点A、B、C、D、E都是圆O上的点， $\overset{⌢}{A C} = \overset{⌢}{A E}$ ， ∠B＝116°，则∠D的度数为度．

查看试题解析
13. 如图，点A、B在反比例函数 $y = \frac{k}{x}$ （ $k > 0$ ， $x > 0$ ）的图象上，AC⊥x轴于点C，BD⊥x轴于点D，BE⊥y轴于点E，连接AE．若OE＝1， $O C = \frac{2}{3} O D$ ， AC＝AE，则k的值为．

查看试题解析
14. 如图，半径为 2 的⊙O 与正六边形 ABCDEF 相切于点 C，F，则图中阴影部分的面积为.

查看试题解析

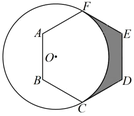
三、解答题

15. 请用圆规、直尺作图，不写作法，但要保留作图痕迹．
已知：如图，Rt△ABC中，∠C＝90°．
求作：一个⊙O，使⊙O与AB、BC所在直线都相切，且圆心O在边AC上．

查看试题解析
16.

(1)、计算： $\sqrt{24} + {(π + 7)}^{0} + {(- 2)}^{3} \times {(\frac{1}{2})}^{2}$

(2)、化简： ${(a - 5)}^{2} + \frac{1}{2} a (2 a + 8)$ ．

查看试题解析
17. 如图，可以自由转动的均匀的两个转盘，被它的半径分成标有数字的扇形区域，扇形圆心角的度数如图所示，小亮和小颖做游戏，规则如下：同时转动这两个转盘，待转盘自动停止后，指针指向扇形内部，则该扇形内部的数字即为转出的结果（若指针指向两个扇形的交线，则此次转动无效，重新转动，直到两个转盘的指针均指向扇形的内部为止）．若两个转盘所转得的数字乘积为1，则小亮赢，否则小颖赢．这个游戏公平吗？请用画树状图或列表法说明理由．

查看试题解析
18. 小刚和小华约定一同去公园游玩，如图，公园有南北两个门，北门A在南门B的正北方向，小刚自公园北门A处出发，沿南偏东30°方向前往游乐场D处：小华自南门B处出发，沿正东方向行走150m到达C处，再沿北偏东22.6°方向前往游乐场D处与小明汇合（如图所示），两人所走的路程相同．求公园北门A与南门B之间的距离．（结果取整数．参考数据： $s i n 22.6 ° \approx \frac{5}{13}$ ， $c o s 22.6 ° \approx \frac{12}{13}$ ， $t a n 22.6 ° \approx \frac{5}{12}$ ， $\sqrt{3} \approx 1.73$ ）

查看试题解析
19. 4月23日是世界读书日，习近平说：“读书可以让人保持思想活力，让人得到智慧启发，让人滋养浩然之气．”某校文学社为了解学生课外阅读情况，对本校初一年级的学生进行了课外阅读知识水平检测．为了解情况，从初一年级随机抽取部分女生和男生的测试成绩，这些学生的成绩记为x（ $0 \leq x \leq 100$ ），将所得数据分为5组：
A组： $x < 60$ ， B组： $60 \leq x < 70$ ， C组： $70 \leq x < 80$ ， D组： $80 \leq x < 90$ ， E组： $90 \leq x \leq 100$ ．
学校对数据进行分析后，提供了如下信息：
女生成绩在 $70 \leq x < 80$ 这一组的数据是：70，72，72，72；
男生成绩在 $60 \leq x < 80$ 这一组的数据是：72，68，62，68，70；
抽取的男生和女生测试成绩的平均数、中位数、众数如表所示：

平均数
中位数
众数
男生
76
a
68
女生
76
72
b
请根据以上信息解答下列问题：

(1)、a＝， b＝，请补全条形统计图；

(2)、通过以上的数据分析，你认为（填“男”或“女”）学生的课外阅读整体水平较高，请说明理由：．（写出一条理由即可）

查看试题解析
20. 今年，“广汉三星堆”又有新的文物出土，景区游客大幅度增长.为了应对暑期旅游旺季，方便更多的游客在园区内休息，景区管理委员会决定向某公司采购一批户外休闲椅.经了解，该公司出售弧形椅和条形椅两种类型的休闲椅，已知条形椅的单价是弧形椅单价的0.75倍，用8000元购买弧形椅的数量比用4800元购买条形椅的数量多10张.

(1)、弧形椅和条形椅的单价分别是多少元？

(2)、已知一张弧形椅可坐5人，一张条形椅可坐3人，景区计划共购进300张休闲椅，并保证至少增加1200个座位.请问：应如何安排购买方案最节省费用？最低费用是多少元？

查看试题解析
21. 已知：在Rt△ABC中，∠BAC=90°，D是BC的中点，E是AD的中点．过点A作AF∥BC交BE的延长线于点F

(1)、求证：△AEF≌△DEB；

(2)、当△ABC满足什么条件时，四边形ADCF是正方形？请说明理由．

查看试题解析
22. “互联网＋”时代，网上购物备受消费者青睐，某网店出售一款电子玩具，其成本为每件80元，当售价为每件140元时，每月可销售100件．为了扩大销量，该网店采取降价措施，据市场调查：销售单价每降低1元，每月可多销售5件，设每件电子玩具的售价为x元（x为正整数），每月销售量为y件．

(1)、直接写出y与x之间的函数关系式；（不需解答过程）

(2)、设该网店每月销售这款产品获得的利润为w元，求当销售单价降低多少元时，每月销售这款产品获得的利润最大，最大利润是多少元；

(3)、该网店店主决定每月从这款产品的销售利润中捐出500元资助贫困学生，为保证捐款后这款产品的每月销售利润不低于5500元，且让消费者得到最大的实惠，该如何确定该电子玩具的价格？请说明理由．

查看试题解析
23. 问题提出：某段楼梯共有10个台阶，如果某同学在上台阶时，可以一步1个台阶，也可以一步2个台阶．那么该同学从该段楼梯底部上到顶部共有多少种不同的走法？
问题探究：
为解决上述实际问题，我们先建立如下数学模型：
如图①，用若干个边长都为1的正方形（记为1×1矩形）和若干个边长分别为1和2的矩形（记为1×2矩形），要拼成一个如图②中边长分别为1和n的矩形（记为1×n矩形），有多少种不同的拼法？（设 $A_{1 \times n}$ 表示不同拼法的个数）
为解决上述数学模型问题，我们采取的策略和方法是：一般问题特殊化，
探究一：先从最特殊的情形入手，即要拼成一个1×1矩形，有多少种不同拼法？
显然，只有1种拼法，如图③，即 $A_{1 \times 1} = 1$ 种．
探究二：要拼成一个1×2矩形，有多少种不同拼法？
可以看出，有2种拼法，如图④，即 ${A_{1}}_{\times 2} = 2$ 种．
探究三：要拼成一个1×3矩形，有多少种不同拼法？
拼图方法可分为两类：一类是在图④这2种1×2矩形上方，各拼上一个1×1矩形，即这类拼法共有2种；另一类是在图③这1种1×1矩形上方拼上一个1×2矩形，即这类拼法有1种．如图⑤，即 $A_{1 \times 3} = 2 + 1 = 3$ （种）．

(1)、探究四：仿照上述探究过程，要拼成一个1×4矩形，有多少种不同拼法？请画示意图说明，并求出结果．

(2)、探究五：
要拼成一个1×5矩形，有 $A_{1 \times 5} =$ 种不同拼法．（直接写出结果，不需画图）
要拼成一个1×6矩形，有 $A_{1 \times 6} =$ 种不同拼法．（直接写出结果，不需画图）
要拼成一个1×7矩形，有 $A_{1 \times 7} =$ 种不同拼法．（直接写出结果，不需画图）
问题解决：
某段楼梯共有10个台阶，如果某同学在上台阶时，可以一步1个台阶，也可以一步2个台阶．那么该同学从该段楼梯底部上到项部共有种不同的走法．（直接写出结果，不需画图）

查看试题解析
24. 已知：如图，在△AED中，AD＝10cm，∠AED＝90°，延长AE到点B，使DE＝EB＝8cm，过点B作CB⊥AB，CB＝2cm，连接CD；点N从点A出发，沿AD方向匀速运动，速度为1cm/s；过点N作NF⊥AE，以DE和EF为邻边作矩形DEFG，点M与点N同时出发，点M从点B沿BA方向匀速运动，速度为1cm/s，连接MN、MD、MC，设运动时间为t（s）（ $0 < t < 8$ ）．解答下列问题：

(1)、当E在线段MF的垂直平分线上时，求t的值；

(2)、设四边形MNGD的面积为S（ $c m^{2}$ ），求S与t的函数关系式；

(3)、在运动过程中，是否存在某一时刻t，使点M在∠DNF的角平分线上，若存在，求出t的值；若不存在，请说明理由．

(4)、连接AC，当t＝时，直线MN过线段AC的中点O．

查看试题解析

	平均数	中位数	众数
男生	76	a	68
女生	76	72	b