山东省青岛市南区2022年中考九年级二摸数学试题
试卷更新日期:2022-05-31 类型:中考模拟
一、单选题
-
1. 的绝对值是( )A、 B、 C、 D、2. 用肥皂水吹泡泡,共泡沫的厚度约0.000 326毫米,用科学记数法表示为( )A、毫米 B、毫米 C、厘米 D、米3. 如图所示,用木板制作的“中”字的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 如图,在⊙O中,∠BAC=15°,∠ADC=20°,则∠ABO的度数为( )
4. 如图,在⊙O中,∠BAC=15°,∠ADC=20°,则∠ABO的度数为( ) A、70° B、55° C、45° D、35°5. 某班有40人,一次体能测试后,老师对测试成绩进行了统计.由于小亮没有参加本次集体测试,因此计算其他39人的平均分为90分,方差 . 后来小亮进行了补测,成绩为90分,关于该班40人的测试成绩,下列说法正确的是( )A、平均分不变,方差变大 B、平均分不变,方差变小 C、平均分和方差都不变 D、平均分和方差都改变6. 如图,将正方形网格放置在平面直角坐标系中,其中每个小正方形的边长均为1, 经过平移后得到 ,若 上一点 平移后对应点为 ,点 绕原点顺时针旋转 ,对应点为 ,则点 的坐标为( )
A、70° B、55° C、45° D、35°5. 某班有40人,一次体能测试后,老师对测试成绩进行了统计.由于小亮没有参加本次集体测试,因此计算其他39人的平均分为90分,方差 . 后来小亮进行了补测,成绩为90分,关于该班40人的测试成绩,下列说法正确的是( )A、平均分不变,方差变大 B、平均分不变,方差变小 C、平均分和方差都不变 D、平均分和方差都改变6. 如图,将正方形网格放置在平面直角坐标系中,其中每个小正方形的边长均为1, 经过平移后得到 ,若 上一点 平移后对应点为 ,点 绕原点顺时针旋转 ,对应点为 ,则点 的坐标为( )
A、 B、 C、 D、7. 如图,矩形的顶点A,B,C分别落在的边 , 上,若 , 要求只用无刻度的直尺作的平分线,小明的作法如下:连接 , 交于点E,作射线 , 则射线平分 , 有以下几条几何性质:①矩形的四个角都是直角;②矩形的对角线互相平分;③等腰三形的“三线合一”;④角平分线上的点到角两边的距离相等.小明的作法依据是( ) A、①②④ B、③④ C、②③④ D、②③8. 如图,一次函数y1=x与二次函数y2=ax2+bx+c图象相交于P、Q两点,则函数y=ax2+(b-1)x+c的图象可能是( )
A、①②④ B、③④ C、②③④ D、②③8. 如图,一次函数y1=x与二次函数y2=ax2+bx+c图象相交于P、Q两点,则函数y=ax2+(b-1)x+c的图象可能是( )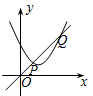 A、
A、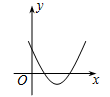 B、
B、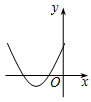 C、
C、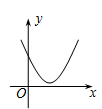 D、
D、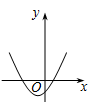
二、填空题
-
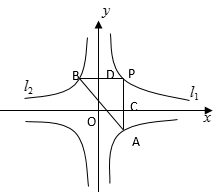
9. 计算: .10. 某公司在2009年的盈利额为200万元,预计2011年的盈利额将达到242万元,若每年比上一年盈利额增长的百分率相同,那么该公司在2010年的盈利额为万元.11. 如图,两个反比例函数和的图像分别是和 . 设点P在上,PC⊥x轴,交于点A.PD⊥x轴,交于点B,则△PAB的面积为 .
 12. 如图,在中, , , , 将绕点O顺时针旋转后得 , 将线段绕点E逆时针旋转后得线段 , 分别以O,E为圆心,、长为半径画弧和弧 , 连接 , 则图中阴影部分面积是 .
12. 如图,在中, , , , 将绕点O顺时针旋转后得 , 将线段绕点E逆时针旋转后得线段 , 分别以O,E为圆心,、长为半径画弧和弧 , 连接 , 则图中阴影部分面积是 . 13. 如图,已知P为线段上一点, , , 分别以 , 为边在的同侧作菱形和菱形 , 点P,C,E在一条直线上, . M,N分别是对角线 , 的中点,则线段的长为 .
13. 如图,已知P为线段上一点, , , 分别以 , 为边在的同侧作菱形和菱形 , 点P,C,E在一条直线上, . M,N分别是对角线 , 的中点,则线段的长为 . 14. 如图,在以 为直角顶点的等腰直角三角形纸片 中,将 角折起,使点 落在 边上的点 (不与点 , 重合)处,折痕是 .
14. 如图,在以 为直角顶点的等腰直角三角形纸片 中,将 角折起,使点 落在 边上的点 (不与点 , 重合)处,折痕是 .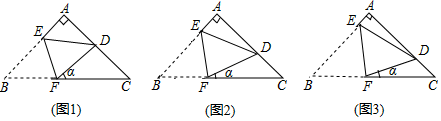
如图,当 时, ;
如图,当 时, ;
如图,当 时, ;
……
依此类推,当 ( 为正整数)时, .
三、解答题
-
15. 已知: .
求作: , 使得 , .
 16.(1)、解不等式组:(2)、化简:17. 我市某校为了让学生的课余生活丰富多彩,开展了以下课外活动:
16.(1)、解不等式组:(2)、化简:17. 我市某校为了让学生的课余生活丰富多彩,开展了以下课外活动:A
经典诵读与写作
B
数学兴趣与培优
C
英语阅读与写作
D
艺体类
E
其他
为了了解学生的选择情况(每名学生均按要求选择了其中一项),现从该校随机抽取了部分学生进行问卷调查,并根据调查得到的数据绘制了如图所示的两幅不完整的统计图.请根据统计图提供的信息回答下列问题:
 (1)、此次共调查了名学生;(2)、将条形统计图补充完整;(3)、“数学兴趣与培优”对应扇形的圆心角的度数为;(4)、若该校共有2000名学生,请估计该校喜欢A,B,C三类活动的学生共有多少人.18. 某大桥采用H型塔型斜拉桥结构(如甲图),图乙是从图甲抽象出的平面图.测得拉索与水平桥面的夹角是 , 拉索与水平桥面的夹角是 , 两拉索顶端的距离为2米,两拉索底端距离为10米,请求出立柱的长(结果精确到1米).
(1)、此次共调查了名学生;(2)、将条形统计图补充完整;(3)、“数学兴趣与培优”对应扇形的圆心角的度数为;(4)、若该校共有2000名学生,请估计该校喜欢A,B,C三类活动的学生共有多少人.18. 某大桥采用H型塔型斜拉桥结构(如甲图),图乙是从图甲抽象出的平面图.测得拉索与水平桥面的夹角是 , 拉索与水平桥面的夹角是 , 两拉索顶端的距离为2米,两拉索底端距离为10米,请求出立柱的长(结果精确到1米).(参考数据: , , )
 19. 有四张反面完全相同的纸牌 , 其正面分别画有四个不同的几何图形,将四张纸牌洗匀正面朝下随机放在桌面上.
19. 有四张反面完全相同的纸牌 , 其正面分别画有四个不同的几何图形,将四张纸牌洗匀正面朝下随机放在桌面上. (1)、从四张纸牌中随机摸出一张,摸出的牌面图形是中心对称图形的概率是 .(2)、小明和小亮约定做一个游戏,其规则为:先由小明随机摸出一张,不放回.再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张牌面图形既是轴对称图形又是中心对称图形,则小亮获胜,否则小明获胜.这个游戏公平吗?请用列表法(或画树状图)说明理由.(纸牌用表示)若不公平,请你帮忙修改一下游戏规则,使游戏公平.20. 文美书店准备购进甲、乙两种图书共1200本进行销售.已知甲、乙两种图书的进价分别为每本20元、14元,不同方案甲、乙两种图书的购进数量和售完后总收入的对应关系如下表所示:
(1)、从四张纸牌中随机摸出一张,摸出的牌面图形是中心对称图形的概率是 .(2)、小明和小亮约定做一个游戏,其规则为:先由小明随机摸出一张,不放回.再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张牌面图形既是轴对称图形又是中心对称图形,则小亮获胜,否则小明获胜.这个游戏公平吗?请用列表法(或画树状图)说明理由.(纸牌用表示)若不公平,请你帮忙修改一下游戏规则,使游戏公平.20. 文美书店准备购进甲、乙两种图书共1200本进行销售.已知甲、乙两种图书的进价分别为每本20元、14元,不同方案甲、乙两种图书的购进数量和售完后总收入的对应关系如下表所示:方案一
方案二
购进数量(本)
甲种图书
600
400
乙种图书
600
800
售完后总收入(元)
28800
27200
(1)、甲、乙两种图书的售价分别为每本多少元?(2)、书店决定用不多于20000元来购进这1200本图书,为了让利读者,实际销售甲种图书售价每本降低3元,乙种图书售价每本降低2元,问书店应如何进货才能获得大利润?(购进的两种图书全部销售完.)21. 已知:如图,正方形的对角线相交于点O,的平分线分别交 , 于点E,F,作于点H,分别交 , 于点G,P,连接 , . (1)、求证:;(2)、判断四边形是什么特殊四边形?并证明你的结论.22. 某超市销售一种文具,进价为5元/件.售价为6元/件时,当天的销售量为100件.在销售过程中发现:售价每上涨0.5元,当天的销售量就减少5件.设当天销售单价统一为 元/件( ,且 是按0.5元的倍数上涨),当天销售利润为 元.(1)、求 与 的函数关系式(不要求写出自变量的取值范围);(2)、要使当天销售利润不低于240元,求当天销售单价所在的范围;(3)、若每件文具的利润不超过 ,要想当天获得利润最大,每件文具售价为多少元?并求出最大利润.23. 新定义:如图1,在长方形中,点O为边上的一点(不与A、D重合).若一个小球从点O出发,依次在长方形各边上经过n次反弹后恰好回到点O(反弹点分别为、、、……、 , 且每次反弹的入射角等于反射角).设此时的 , 则称k的值为n次完美反弹比(且n为奇数),
(1)、求证:;(2)、判断四边形是什么特殊四边形?并证明你的结论.22. 某超市销售一种文具,进价为5元/件.售价为6元/件时,当天的销售量为100件.在销售过程中发现:售价每上涨0.5元,当天的销售量就减少5件.设当天销售单价统一为 元/件( ,且 是按0.5元的倍数上涨),当天销售利润为 元.(1)、求 与 的函数关系式(不要求写出自变量的取值范围);(2)、要使当天销售利润不低于240元,求当天销售单价所在的范围;(3)、若每件文具的利润不超过 ,要想当天获得利润最大,每件文具售价为多少元?并求出最大利润.23. 新定义:如图1,在长方形中,点O为边上的一点(不与A、D重合).若一个小球从点O出发,依次在长方形各边上经过n次反弹后恰好回到点O(反弹点分别为、、、……、 , 且每次反弹的入射角等于反射角).设此时的 , 则称k的值为n次完美反弹比(且n为奇数),设长方形中, , .


 (1)、问题提出:当时,k与x、y之间有什么等量关系呢?
(1)、问题提出:当时,k与x、y之间有什么等量关系呢?探究1:设每个小正方形的边长均为1.
①如图2,在长方形中, , . 若小球从格点O出发,依次在、、边上经过3次反弹后恰好回到点O,显然,此时 .
②如图3,在长方形中, , . 若小球从格点O出发,依次在、、边上经过3次反弹后恰好回到点O,显然,此时 .
③如图4,在长方形中, , , 若小球从格点O出发,依次在、、边上经过3次反弹后恰好回到点O,请在图3中用、、标记每条边上的反弹点,并画出小球每次反弹的轨迹,再直接写出此时k=…….
……
(2)、问题解决1:通过归纳,时,k与x、y间的等量关系为: .
(3)、①探究2:当时,k与x、y之间又有什么等量关系呢?当时,有图5、图6两种情况.请直按写出k与x、y之间所有可能的等量关系: .
②请直接写出当时,k与x、y之间所有可能的等量关系: .
(4)、问题解决2:若长方形中,k为该长方形的n次完美反弹比(且n为奇数),请直接写出k与n、x、y之间所有可能的等量关系: .
24. 已知:如图,在中, , cm,cm.点D是中点,点P从点C出发,沿向点A匀速运动,速度为2cm/s;同时点Q从点A出发,沿向点B匀速运动,速度为3cm/s;连接 , , , 将绕点D旋转得 , 连接 , . 设运动时间为t(s) , 解答下列问题: (1)、当t为何值时,?(2)、当t为何值时,四边形是菱形?(3)、设四边形的面积为y(cm2),求y与t的函数关系式;(4)、是否存在某一时刻t,使得点T在的外接圆上?若存在,求出t的值;若不存在,请说明理由.
(1)、当t为何值时,?(2)、当t为何值时,四边形是菱形?(3)、设四边形的面积为y(cm2),求y与t的函数关系式;(4)、是否存在某一时刻t,使得点T在的外接圆上?若存在,求出t的值;若不存在,请说明理由.