山东省青岛市2022年九年级下学期第二次质量检测数学试题
试卷更新日期:2022-05-31 类型:中考模拟
一、单选题
-
1. 0.000345用科学记数法表示为( )A、0.345×10﹣3 B、3.45×104 C、3.45×10﹣4 D、34.5×10﹣52. 观察下列图形,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图中几何体的主视图为( )
3. 如图中几何体的主视图为( ) A、
A、 B、
B、 C、
C、 D、
D、 4. 下列运算中,计算正确的是( )A、 B、 C、 D、5. 在平面直角坐标系中,把点P(-3,1)向右平移5个单位得到点P1 , 再将点P1绕原点旋转90°得到点P2 , 则点P2的坐标是( )
4. 下列运算中,计算正确的是( )A、 B、 C、 D、5. 在平面直角坐标系中,把点P(-3,1)向右平移5个单位得到点P1 , 再将点P1绕原点旋转90°得到点P2 , 则点P2的坐标是( ) A、(-1,2) B、(1,-2) C、(2,1)或(1,-2) D、(-1,2)或(1,-2)6. 如图,AB是的直径,BC是的切线,点B为切点,若 , , 则劣弧BD的长为( )
A、(-1,2) B、(1,-2) C、(2,1)或(1,-2) D、(-1,2)或(1,-2)6. 如图,AB是的直径,BC是的切线,点B为切点,若 , , 则劣弧BD的长为( ) A、cm B、cm C、cm D、cm7. 如图,矩形ABCD中,AB=12,点E是AD上的一点,AE=6,BE的垂直平分线交BC的延长线于点F , 连接EF交CD于点G , 若G是CD的中点,则BC的长是( )
A、cm B、cm C、cm D、cm7. 如图,矩形ABCD中,AB=12,点E是AD上的一点,AE=6,BE的垂直平分线交BC的延长线于点F , 连接EF交CD于点G , 若G是CD的中点,则BC的长是( )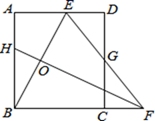 A、12.5 B、12 C、10 D、10.58. 在同一坐标系中,二次函数 与一次函数 的图像可能是( )A、
A、12.5 B、12 C、10 D、10.58. 在同一坐标系中,二次函数 与一次函数 的图像可能是( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
9. 计算: = .10. 在一个不透明的袋中装有除颜色外其余均相同的n个小球,其中有5个黑球,从袋中随机摸出一球,记下其颜色,这称为一次摸球试验,之后把它放回袋中,搅匀后,再继续摸出一球,以下是利用计算机模拟的摸球试验次数与摸出黑球次数的列表:
摸球试验次数
100
1000
5000
10000
50000
100000
摸出黑球次数
46
487
2506
5008
24996
50007
根据列表,可以估计出n的值是 .
11. 一元二次方程 有两个相等的实数根,点 、 是反比例函数 上的两个点,若 ,则 (填“<”或“>”或“=”).12. 新冠疫情期间,小李同学连续两周居家健康检测,如下图是小李记录的体温情况折线统计图,记第一周体温的方差为 , 第二周体温的方差为 , 试判断两者之间的大小关系(用“>”、“=”、“<”填空).小李连续两周居家体温测量折线统计图
 13. 如图,已知在矩形ABCD中,AB=2,以点A为圆心,AD长为半径作 , 交AB于点E,以AB为直径的半圆恰好与DC相切,则图中阴影部分的面积为 .
13. 如图,已知在矩形ABCD中,AB=2,以点A为圆心,AD长为半径作 , 交AB于点E,以AB为直径的半圆恰好与DC相切,则图中阴影部分的面积为 .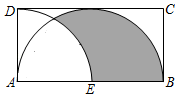 14. 如图,正方形ABCD的边长为a,点E在边AB上运动(不与点A,B重合),∠DAM=45°,点F在射线AM上,且AF= BE,CF与AD相交于点G,连接EC、EF、EG.则下列结论:①∠ECF=45°;②△AEG的周长为(1+ )a;③BE2+DG2=EG2;④△EAF的面积的最大值是 a2;⑤当时BE= a,G是线段AD的中点.其中正确的结论是.
14. 如图,正方形ABCD的边长为a,点E在边AB上运动(不与点A,B重合),∠DAM=45°,点F在射线AM上,且AF= BE,CF与AD相交于点G,连接EC、EF、EG.则下列结论:①∠ECF=45°;②△AEG的周长为(1+ )a;③BE2+DG2=EG2;④△EAF的面积的最大值是 a2;⑤当时BE= a,G是线段AD的中点.其中正确的结论是.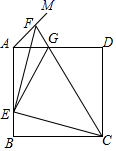
三、解答题
-
15. 尺规作图(要求:不写作法,保留作图痕迹)
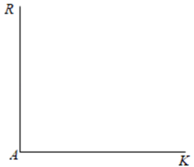
如图,已知线段 , , 垂足为A.
求作: , 使分别与AK、AR相切,圆心O与点A的距离等于a.
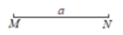
 16. 计算(1)、化简:(2)、解不等式组 , 并写出它的整数解的和.17. 4张相同的卡片上分别写有数字0、1、 、3,将卡片的背面朝上,洗匀后从中任意抽取1张.将卡片上的数字记录下来;再从余下的3张卡片中任意抽取1张,同样将卡片上的数字记录下来.(1)、第一次抽取的卡片上数字是负数的概率为;(2)、小敏设计了如下游戏规则:当第一次记录下来的数字减去第二次记录下来的数字所得结果为非负数时,甲获胜:否则,乙获胜.小敏设计的游戏规则公平吗?为什么?(请用画树状图或列表等方法说明理由).18. 为了倡导“节约用水,从我做起”,某市政府决定对该市直属机关200户家庭用水情况进行调查.市政府调查小组随机抽查了其中部分家庭一年的月平均用水量(单位:吨),调查中发现,每户家庭月平均用水量在3~7吨范围内,并将调查结果制成了如下尚不完整的统计表:
16. 计算(1)、化简:(2)、解不等式组 , 并写出它的整数解的和.17. 4张相同的卡片上分别写有数字0、1、 、3,将卡片的背面朝上,洗匀后从中任意抽取1张.将卡片上的数字记录下来;再从余下的3张卡片中任意抽取1张,同样将卡片上的数字记录下来.(1)、第一次抽取的卡片上数字是负数的概率为;(2)、小敏设计了如下游戏规则:当第一次记录下来的数字减去第二次记录下来的数字所得结果为非负数时,甲获胜:否则,乙获胜.小敏设计的游戏规则公平吗?为什么?(请用画树状图或列表等方法说明理由).18. 为了倡导“节约用水,从我做起”,某市政府决定对该市直属机关200户家庭用水情况进行调查.市政府调查小组随机抽查了其中部分家庭一年的月平均用水量(单位:吨),调查中发现,每户家庭月平均用水量在3~7吨范围内,并将调查结果制成了如下尚不完整的统计表:月平均用水量(吨)
3
4
5
6
7
频数(户数)
4
a
9
10
7
频率
0.08
0.40
b
c
0.14
请根据统计表中提供的信息解答下列问题:
(1)、填空:a= , b= .(2)、这些家庭中月平均用水量数据的平均数是 , 众数是 , 中位数是 .(3)、根据样本数据,估计该市直属机关200户家庭中月平均用水量不超过5吨的约有户.19. 如图,为了测量河对岸两点A,B之间的距离,在河岸这边取点C,D.测得CD=80m, , , , . 设A,B,C,D在同一平面内, (1)、求AC的长;(2)、求A,B两点之间的距离.(参考数据: , . )20. 在抗击“新冠肺炎”战役中,某公司接到转产生产1440万个医用防护口罩补充防疫一线需要的任务,临时改造了甲、乙两条流水生产线.试产时甲生产线每天的产能(每天的生产的数量)是乙生产线的2倍,各生产80万个,甲比乙少用了2天.(1)、求甲、乙两条生产线每天的产能各是多少?(2)、若甲、乙两条生产线每天的运行成本分别是1.2万元和0.5万元,要使完成这批任务总运行成本不超过40万元,则至少应安排乙生产线生产多少天?21. 如图,在四边形 中, , , , 交 于点 ,过点 作 ,垂足为 ,且 .
(1)、求AC的长;(2)、求A,B两点之间的距离.(参考数据: , . )20. 在抗击“新冠肺炎”战役中,某公司接到转产生产1440万个医用防护口罩补充防疫一线需要的任务,临时改造了甲、乙两条流水生产线.试产时甲生产线每天的产能(每天的生产的数量)是乙生产线的2倍,各生产80万个,甲比乙少用了2天.(1)、求甲、乙两条生产线每天的产能各是多少?(2)、若甲、乙两条生产线每天的运行成本分别是1.2万元和0.5万元,要使完成这批任务总运行成本不超过40万元,则至少应安排乙生产线生产多少天?21. 如图,在四边形 中, , , , 交 于点 ,过点 作 ,垂足为 ,且 . (1)、求证:四边形 是菱形;(2)、若 ,求 的面积.22. 甲秀楼是贵阳市一张靓丽的名片.如图①,甲秀楼的桥拱截面 可视为抛物线的一部分,在某一时刻,桥拱内的水面宽 ,桥拱顶点 到水面的距离是 .
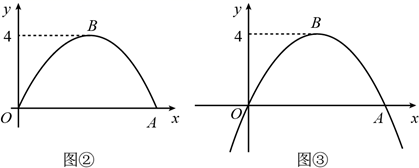
(1)、求证:四边形 是菱形;(2)、若 ,求 的面积.22. 甲秀楼是贵阳市一张靓丽的名片.如图①,甲秀楼的桥拱截面 可视为抛物线的一部分,在某一时刻,桥拱内的水面宽 ,桥拱顶点 到水面的距离是 .
 (1)、按如图②所示建立平面直角坐标系,求桥拱部分抛物线的函数表达式;(2)、一只宽为 的打捞船径直向桥驶来,当船驶到桥拱下方且距 点 时,桥下水位刚好在 处.有一名身高 的工人站立在打捞船正中间清理垃圾,他的头顶是否会触碰到桥拱,请说明理由(假设船底与水面齐平);(3)、如图③,桥拱所在的函数图象是抛物线 ,该抛物线在 轴下方部分与桥拱 在平静水面中的倒影组成一个新函数图象.将新函数图象向右平移 个单位长度,平移后的函数图象在 时, 的值随 值的增大而减小,结合函数图象,求 的取值范围.23. 通过构造恰当的图形,可以对线段长度、图形面积大小等进行比较,直观地得到一些不等关系或最值,这是“数形结合”思想的典型应用.
(1)、按如图②所示建立平面直角坐标系,求桥拱部分抛物线的函数表达式;(2)、一只宽为 的打捞船径直向桥驶来,当船驶到桥拱下方且距 点 时,桥下水位刚好在 处.有一名身高 的工人站立在打捞船正中间清理垃圾,他的头顶是否会触碰到桥拱,请说明理由(假设船底与水面齐平);(3)、如图③,桥拱所在的函数图象是抛物线 ,该抛物线在 轴下方部分与桥拱 在平静水面中的倒影组成一个新函数图象.将新函数图象向右平移 个单位长度,平移后的函数图象在 时, 的值随 值的增大而减小,结合函数图象,求 的取值范围.23. 通过构造恰当的图形,可以对线段长度、图形面积大小等进行比较,直观地得到一些不等关系或最值,这是“数形结合”思想的典型应用.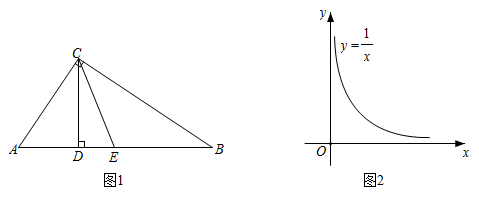 (1)、【理解】
(1)、【理解】如图1, , 垂足分别为C、D,E是的中点,连接 . 已知 , .
①分别求线段、的长(用含a、b的代数式表示);
②比较大小: ▲ (填“<”、“=”或“>”),并用含a、b的代数式表示该大小关系.
(2)、【应用】如图2,在平面直角坐标系中,点M、N在反比例函数的图像上,横坐标分别为m、n.设 , 记 .
①当时, ▲ ;当时, ▲ ;
②通过归纳猜想,可得l的最小值是 ▲ . 请利用图2构造恰当的图形,并说明你的猜想成立.
24. 如图,已知Rt△OAB, , , 斜边cm,将Rt△OAB绕点O顺时针旋转60°,得到△ODC,连接BC.点M从点D出发,沿DB方向匀速行动,速度为1cm/s;同时,点N从点O出发,沿OC方向匀速运动,速度为2cm/s;当一个点停止运动,另一个点也停止运动,连接AM,MN,MN交CD于点P.设运动时间为t(s) , 解答下列问题: (1)、当t为何值时,OM平分?(2)、设四边形AMNO的面积为S(cm2),求S与t的函数关系式;(3)、在运动过程中,当时,求四边形AMNO的面积;(4)、在运动过程中,是否存在某一时刻t,使点P为线段CD的中点?若存在,求出t的值;若不存在,请说明理由.
(1)、当t为何值时,OM平分?(2)、设四边形AMNO的面积为S(cm2),求S与t的函数关系式;(3)、在运动过程中,当时,求四边形AMNO的面积;(4)、在运动过程中,是否存在某一时刻t,使点P为线段CD的中点?若存在,求出t的值;若不存在,请说明理由.