山东省聊城市莘县2022年中考二模数学试题

试卷更新日期：2022-05-31 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列算式中，运算结果为负数的是（）

A、 $- (- 2)$ B、 $| - 2 |$ C、 $- 2^{2}$ D、 ${(- 2)}^{2}$

查看试题解析
2. 桌上摆放着一个由相同正方体组成的组合体，其俯视图如图所示，图中数字为该位置小正方体的个数，则这个组合体的左视图为（）

A、 B、 C、 D、

查看试题解析
3. 小明同学对数据26，36，36，46，5■，52进行统计分析．发现其中一个两位数的个位数字被墨水涂污看不到了，则计算结果与被涂污数字无关的是（）

A、平均数 B、方差 C、中位数 D、众数

查看试题解析
4. 某种计算机完成一次基本运算的时间约为1纳秒 $(n s)$ ，已知1纳秒 $= 0.000 000 001$ 秒，该计算机完成15次基本运算，所用时间用科学记数法表示为（）

A、 $1.5 \times 10^{- 9}$ 秒 B、 $15 \times 10^{- 3}$ 秒 C、 $1.5 \times 10^{- 8}$ 秒 D、 $15 \times 10^{- 8}$ 秒

查看试题解析
5. 一次函数y=ax+b与反比例函数 $y = \frac{a - b}{x}$ ，其中ab＜0，a、b为常数，它们在同一坐标系中的图象可以是（　　）

A、 B、 C、 D、

查看试题解析
6. 正方形ABCD的边长为2，以各边为直径在正方形内画半圆，得到如图所示阴影部分，若随机向正方形ABCD内投一粒米，则米粒落在阴影部分的概率为（　　）

A、 $\frac{π - 2}{2}$ B、 $\frac{π - 2}{4}$ C、 $\frac{π - 2}{8}$ D、 $\frac{π - 2}{16}$

查看试题解析
7. 如图，在长方形纸片 $A B C D$ 中， $A B = 8 c m$ ， $A D = 6 c m$ . 把长方形纸片沿直线 $A C$ 折叠，点B落在点E处， $A E$ 交 $D C$ 于点F，则 $A F$ 的长为（）

A、 $\frac{25}{4} c m$ B、 $\frac{15}{2} c m$ C、 $7 c m$ D、 $\frac{13}{2} c m$

查看试题解析
8. 若分式方程 $\frac{3 x - a}{x^{2} - 2 x} + \frac{1}{x - 2} = \frac{2}{x}$ 有增根，则实数a的取值是（）

A、0或2 B、4 C、8 D、4或8

查看试题解析
9. 如图，五边形 $A B C D E$ 是 $⊙ O$ 的内接正五边形， $A F$ 是 $⊙ O$ 的直径，则 $∠ B D F$ 的度数是（）

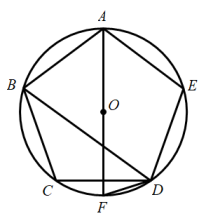A、18° B、36° C、 $54 °$ D、72°

查看试题解析
10. 若关于 $x$ 的一元一次不等式组 ${\begin{array}{l} \frac{2}{3} x > x - 1 \\ 4 x + 1 \geq a \end{array}$ 恰有3个整数解，且一次函数 $y = (a - 2) x + a + 1$ 不经过第三象限，则所有满足条件的整数 $a$ 的值之和是（　　　）

A、 $- 2$ B、 $- 1$ C、0 D、1

查看试题解析
11. 如图，已知A（3，1）与B（1，0），PQ是直线 $y = x$ 上的一条动线段且 $P Q = \sqrt{2}$ （Q在P的下方），当AP+PQ+QB最小时，Q点坐标为（）

A、（ $\frac{2}{3}$ ， $\frac{2}{3}$ ） B、（ $\frac{\sqrt{2}}{3}$ ， $\frac{\sqrt{2}}{3}$ ） C、（0，0） D、（1，1）

查看试题解析
12. 如图，已知二次函数y＝ax²+bx+c的图象与x轴相交于A，B两点，与y轴交于点C，OA=OC，对称轴为直线x＝1，则下列结论：①abc＜0；②a+ $\frac{1}{2}$ b+ $\frac{1}{4}$ c＝0；③ac+b+1=0；④2+c是关于x的一元二次方程ax²+bx+c＝0的一个根，其中正确的有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 已知 $y = \sqrt{4 - x} + \sqrt{x - 4} + \frac{3}{8}$ ，则 $\sqrt{x y} =$ ．

查看试题解析
14. 如图，这是某同学用纸板做成的一个底面直径为10cm，高为12cm的无底圆锥形玩具(接缝忽略不计)，则做这个玩具所需纸板的面积是cm²(结果保留 $π$ )．

查看试题解析
15. 如图， $A B$ 为半圆的直径，且 $A B = 6$ ，将半圆绕点A顺时针旋转 $6 0^{∘}$ ，点B旋转到点C的位置，则图中阴影部分的面积为．

查看试题解析
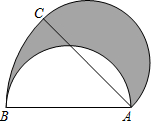16. 如图，已知在平面直角坐标系xOy中，Rt△OAB的直角顶点B在x轴的正半轴上，点A在第一象限，反比例函数y＝ $\frac{k}{x}$ （x＞0）的图象经过OA的中点C．交AB于点D，连结CD．若△ACD的面积是2，则k的值是．

查看试题解析
17. 如图，菱形 $A B C D$ 中， $∠ A B C = 120 °$ ， $A B = 1$ ，延长 $C D$ 至 $A_{1}$ ，使 $D A_{1} = C D$ ，以 $A_{1} C$ 为一边，在 $B C$ 的延长线上作菱形 $A_{1} C C_{1} D_{1}$ ，连接 $A A_{1}$ ，得到 $Δ A D A_{1}$ ；再延长 $C_{1} D_{1}$ 至 $A_{2}$ ，使 $D_{1} A_{2} = C_{1} D_{1}$ ，以 $A_{2} C_{1}$ 为一边，在 $C C_{1}$ 的延长线上作菱形 $A_{2} C_{1} C_{2} D_{2}$ ，连接 $A_{1} A_{2}$ ，得到 $Δ A_{1} D_{1} A_{2}$ ……按此规律，得到 $Δ A_{2020} D_{2020} A_{2021}$ ，记 $Δ A D A_{1}$ 的面积为 $S_{1}$ ， $Δ A_{1} D_{1} A_{2}$ 的面积为 $S_{2}$ …… $Δ A_{2020} D_{2020} A_{2021}$ 的面积为 $S_{2021}$ ，则 $S_{2021} =$ ．

查看试题解析

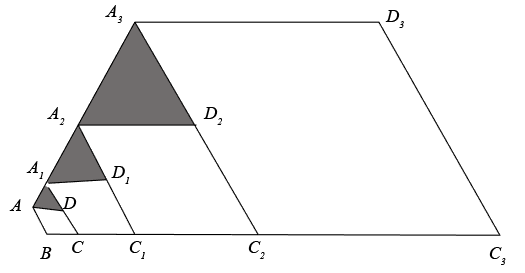
三、解答题

18. 先化简，再求值： $(\frac{2}{a + 1} - \frac{2 a - 3}{a^{2} - 1}) \div \frac{1}{a + 1}$ ，其中 $a = 2 cos 30 ° + {(\frac{1}{2})}^{- 1} - {(π - 3)}^{0}$

查看试题解析
19. 每年6月26日是“国际禁毒日”．某中学为了让学生掌握禁毒知识，提高防毒意识，组织全校学生参加了“禁毒知识网络答题”活动．该校德育处对八年级全体学生答题成绩进行统计，将成绩分为四个等级：优秀、良好、一般、不合格；并绘制成如下不完整的统计图．请你根据图1、图2中所给的信息解答下列问题：

(1)、该校八年级共有名学生，“优秀”所占圆心角的度数为．

(2)、请将图1中的条形统计图补充完整．

(3)、已知该市共有15000名学生参加了这次“禁毒知识网络答题”活动，请以该校八年级学生答题成绩统计情况估计该市大约有多少名学生在这次答题中成绩不合格？

(4)、德育处从该校八年级答题成绩前四名甲、乙、丙、丁学生中随机抽取2名同学参加全市现场禁毒知识竞赛，请用树状图或列表法求出必有甲同学参加的概率．

查看试题解析
20. 如图，在平行四边形 $A B C D$ 中，对角线 $A C$ 与 $B D$ 交于点O，点M，N分别为 $O A$ 、 $O C$ 的中点，延长 $B M$ 至点E，使 $E M = B M$ ，连接 $D E$ ．

(1)、求证： $△ A M B ≌ △ C N D$ ；

(2)、若 $B D = 2 A B$ ，且 $A B = 5$ ， $D N = 4$ ，求四边形 $D E M N$ 的面积．

查看试题解析
21. 某公司投入研发费用80万元（80万元只计入第一年成本），成功研发出一种产品．公司按订单生产（产量=销售量），第一年该产品正式投产后，生产成本为6元/件．此产品年销售量y（万件）与售价x（元/件）之间满足函数关系式y=﹣x+26．

(1)、求这种产品第一年的利润W₁（万元）与售价x（元/件）满足的函数关系式；

(2)、该产品第一年的利润为20万元，那么该产品第一年的售价是多少？

(3)、第二年，该公司将第一年的利润20万元（20万元只计入第二年成本）再次投入研发，使产品的生产成本降为5元/件．为保持市场占有率，公司规定第二年产品售价不超过第一年的售价，另外受产能限制，销售量无法超过12万件．请计算该公司第二年的利润W₂至少为多少万元．

查看试题解析
22. 某兴趣小组为了测量大楼 $C D$ 的高度，先沿着斜坡 $A B$ 走了 $52$ 米到达坡顶点B处，然后在点B处测得大楼顶点C的仰角为 $53 °$ ，已知斜坡 $A B$ 的坡度为 $i = 1 ： 2.4$ ，点A到大楼的距离 $A D$ 为 $72$ 米，求大楼的高度 $C D$ ．（参考数据： $s i n 53 ° \approx \frac{4}{5}$ ， $c o s 53 ° \approx \frac{3}{5}$ ， $t a n 53 ° \approx \frac{4}{3}$ ）

查看试题解析
23. 如图，在平面直角坐标系中，直线AB与y轴交于点 $B (0 ， 7)$ ，与反比例函数 $y = \frac{- 8}{x}$ 在第二象限内的图象相交于点 $A (- 1 ， a)$ ．

(1)、求直线AB的解析式；

(2)、将直线AB向下平移9个单位后与反比例函数的图象交于点C和点E，与y轴交于点D，求 $Δ A C D$ 的面积；

(3)、设直线CD的解析式为 $y = m x + n$ ，根据图象直接写出不等式 $m x + n \leq \frac{- 8}{x}$ 的解集．

查看试题解析
24. 如图，AB是⊙O的直径，点C是 $\overset{⌢}{A B}$ 的中点，连接AC并延长至点D，使CD＝AC，点E是OB上一点，且 $\frac{O E}{E B} = \frac{2}{3}$ ， CE的延长线交DB的延长线于点F，AF交⊙O于点H，连接BH．

(1)、求证：BD是⊙O的切线；

(2)、当OB＝2时，求BH的长．

查看试题解析
25. 如图①，已知抛物线y=ax²+bx+c的图像经过点A（0，3)、B（1，0），其对称轴为直线l：x=2，过点A作AC∥x轴交抛物线于点C，∠AOB的平分线交线段AC于点E，点P是抛物线上的一个动点，设其横坐标为m.

(1)、求抛物线的解析式；

(2)、若动点P在直线OE下方的抛物线上，连结PE、PO，当m为何值时，四边形AOPE面积最大，并求出其最大值；

(3)、如图②，F是抛物线的对称轴l上的一点，在抛物线上是否存在点P使△POF成为以点P为直角顶点的等腰直角三角形？若存在，直接写出所有符合条件的点P的坐标；若不存在，请说明理由.

查看试题解析