山东省聊城市冠县2022年中考二模数学试题

试卷更新日期：2022-05-31 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列各数是负分数的是（）

A、 $- 7$ B、 $\frac{1}{2}$ C、 $- 1.5$ D、0

查看试题解析
2. 如图是由4个相同的小正方体构成的一个组合体，该组合体的三视图中完全相同的是（）

A、主视图和左视图 B、主视图和俯视图 C、左视图和俯视图 D、三个视图均相同

查看试题解析
3. 一个水分子的质量大约为 $3 \times 1 0^{- 23}$ 克，一滴水的质量大约为0.05克．则一滴水大约含（）个水分子．

A、 $1.67 \times 1 0^{21}$ B、 $1.5 \times 1 0^{21}$ C、 $6 \times 1 0^{- 21}$ D、 $1.67 \times 1 0^{25}$

查看试题解析
4. 用尺规作图作三角形的外接圆时，用到了哪些基本作图（）

A、作一条线段等于已知线段 B、作一个角等于已知角 C、作一个角的平分线 D、作一条线段的垂直平分线

查看试题解析
5. 舒青是一名观鸟爱好者，他想要用折线统计图来反映中华秋沙鸭每年秋季到当地避寒越冬的数量变化情况，以下是排乱的统计步骤：①从折线统计图中分析出中华秋沙鸭每年来当地避寒越冬的变化趋势；②从当地自然保护区管理部门收集中华秋沙鸭每年来当地避寒越冬的数量记录；③按统计表的数据绘制折线统计图；④整理中华秋沙鸭每年来当地避寒越冬的数量并制作统计表.正确统计步骤的顺序是（）

A、②→③→①→④ B、③→④→①→② C、①→②→④→③ D、②→④→③→①

查看试题解析
6. 计算 $3^{1}$ ， $3^{2}$ ， $3^{3}$ ， $3^{4}$ ， $3^{5}$ ， $3^{6}$ ，并观察这些幂的个位数字，根据你发现的规律，判断 $3^{2022}$ 的个位数字跟（）的个位数字相同．

A、 $3^{1}$ B、 $3^{2}$ C、 $3^{3}$ D、 $3^{4}$

查看试题解析
7. 关于x的一元二次方程 $5 x^{2} + a (1 - x) = 3 x + 1$ ，如果有一个根为0，那么另一个根为（）

A、1 B、 $\frac{5}{4}$ C、 $\frac{4}{5}$ D、 $- \frac{4}{5}$

查看试题解析
8. 如图，公园内有一个半径为18米的圆形草坪，从A地走到B地有观赏路（劣弧 $A B$ ）和便民路（线段 $A B$ ）.已知A、B是圆上的点，O为圆心， $∠ A O B = 120 °$ ，小强从A走到B，走便民路比走观赏路少走（）米.

A、 $6 π - 6 \sqrt{3}$ B、 $6 π - 9 \sqrt{3}$ C、 $12 π - 9 \sqrt{3}$ D、 $12 π - 18 \sqrt{3}$

查看试题解析
9. 如果不等式组 ${\begin{array}{l} x - b > 0 ， \\ x - b < 1 \end{array}$ 的解集中任何一个x的值均在 $2 \leq x \leq 5$ 的范围内，则b的取值范围是（）

A、 $b < 2$ B、 $2 < b < 4$ C、 $2 < b \leq 4$ D、 $2 \leq b \leq 4$

查看试题解析
10. 如图，已知抛物线y＝ax²+bx+c经过点（﹣1，0），与y轴交于（0，2），且顶点在第一象限，那么下列结论：①a+c=b；②x=-1是方程ax²+bx+c＝0的解；③abc>0；④c﹣a＞2，其中正确的结论为（）

A、①②③ B、②③④ C、①②④ D、①②③④

查看试题解析
11. 图（1），在 $R t △ A B C$ 中， $∠ A = 90 °$ ，点P从点A出发，沿三角形的边以 $1 c m$ /秒的速度逆时针运动一周，图（2）是点P运动时，线段 $A P$ 的长度y（ $c m$ ）随运动时间x（秒）变化的关系图象，则图（2）中P点的坐标是（）

A、 $(13 ， 4.5)$ B、 $(13 ， 4.8)$ C、 $(13 ， 5)$ D、 $(13 ， 5.5)$

查看试题解析
12. 如图，点A，B在反比例函数 $y = \frac{k}{x}$ （ $k > 0$ ， $x > 0$ ）的图象上， $A C ⊥ x$ 轴于点 $C$ ， $B D ⊥ x$ 轴于点D， $B E ⊥ y$ 轴于点E，连结 $A E$ ．若 $O E = 1$ ， $O C = \frac{2}{3} O D$ ， $A C = A E$ ，则k的值为（）

A、2 B、 $\frac{3 \sqrt{2}}{2}$ C、 $\frac{9}{4}$ D、 $2 \sqrt{2}$

查看试题解析

二、填空题

13. $(\sqrt{15} + 2 \sqrt{5}) \div \sqrt{5} =$ ．

查看试题解析
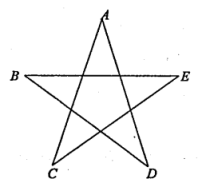
14. 有两把不同的锁和四把钥匙，其中两把钥匙分别能打开这两把锁，另外两把钥匙不能打开这两把锁，随机取出一把钥匙开任意一把锁，一次打开锁的概率是．

查看试题解析
15. 用半径为30，圆心角为120°的扇形纸片围成一个圆锥的侧面，则这个圆锥的底面圆半径为.

查看试题解析
16. 某校用红色灯带制作了一个如图所示的正五角星（A、B、C、D、E是正五边形的五个顶点），则图中 $∠ A$ 的度数是度．

查看试题解析
17. 如图，正方形 $A B C D$ 的边长为4， $⊙ O$ 的半径为1．若 $⊙ O$ 在正方形 $A B C D$ 内平移（ $⊙ O$ 可以与该正方形的边相切），则点A到 $⊙ O$ 上的点的距离的最大值为．

查看试题解析

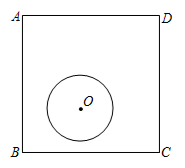
三、解答题

18. 先化简再求值 $(\frac{3 x - 1}{x + 2} - \frac{x - 1}{x + 2}) \div \frac{x}{x^{2} - 4}$ ，其中 $x = 5$ ．

查看试题解析
19. 我市华恒小区居民在“一针疫苗一份心，预防接种尽责任”的号召下，积极联系社区医院进行新冠疫苗接种．为了解接种进度，该小区管理人员对小区居民进行了抽样调查，按接种情况可分如下四类：A类——接种了只需要注射一针的疫苗：B类——接种了需要注射二针，且二针之间要间隔一定时间的疫苗；C类——接种了要注射三针，且每二针之间要间隔一定时间的疫苗；D类——还没有接种，图1与图2是根据此次调查得到的统计图（不完整）．

请根据统计图回答下列问题．

(1)、此次抽样调查的人数是多少人？

(2)、接种B类疫苗的人数的百分比是多少？接种C类疫苗的人数是多少人？

(3)、请估计该小区所居住的18000名居民中有多少人进行了新冠疫苗接种．

(4)、为了继续宣传新冠疫苗接种的重要性，小区管理部门准备在已经接种疫苗的居民中征集2名志愿宣传者，现有3男2女共5名居民报名，要从这5人中随机挑选2人，求恰好抽到一男和一女的概率是多少．

查看试题解析
20. 一张方桌由一个桌面和四条桌脚组成，如果一立方米木材可制作方桌的桌面50个，或制作桌腿300条，现有5立方米木料，那么用多少木料做桌面，用多少木料做桌腿，恰好配成方桌多少张．

查看试题解析
21. 如图，已知M在正方形ABCD的一边BC上，连接AM，并过点M作 $M N ⊥ A M$ ，交正方形ABCD的外角 $∠ D C E$ 的平分线于点N，求证： $A M = M N$ ．

查看试题解析
22. 如图，某无人机爱好者在一小区外放飞无人机，当无人机飞行到一定高度D点处时，无人机测得操控者A的俯角为 $75 °$ ，测得小区楼房 $B C$ 顶端点C处的俯角为 $45 °$ ．已知操控者A和小区楼房 $B C$ 之间的距离为45米，小区楼房 $B C$ 的高度为 $15 \sqrt{3}$ 米．

(1)、求此时无人机的高度；

(2)、在（1）条件下，若无人机保持现有高度沿平行于 $A B$ 的方向，并以5米/秒的速度继续向前匀速飞行．问：经过多少秒时，无人机刚好离开了操控者的视线？（假定点A，B，C，D都在同一平面内．参考数据： $t a n 75 ° = 2 + \sqrt{3}$ ， $t a n 15 ° = 2 - \sqrt{3}$ ．计算结果保留根号）

查看试题解析
23. 如图，一次函数y＝kx+b的图象与y轴的正半轴交于点A，与反比例函数y $= \frac{4}{x}$ 的图象交于P，D两点．以AD为边作正方形ABCD，点B落在x轴的负半轴上，已知△BOD的面积与△AOB的面积之比为1：4．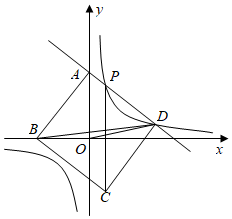

(1)、求一次函数y＝kx+b的表达式；

(2)、求点P的坐标及△CPD外接圆半径的长．

查看试题解析
24. 如图， $△$ ABC是⊙O的内接三角形，过点C作⊙O的切线交BA的延长线于点F，AE是⊙O的直径，连接EC

(1)、求证： $∠ A C F = ∠ B$ ；

(2)、若 $A B = B C$ ， $A D ⊥ B C$ 于点D， $F C = 4$ ， $F A = 2$ ，求 $A D \cdot A E$ 的值

查看试题解析
25. 图，抛物线 $y = a x^{2} - 2 x + c (a \neq 0)$ 与x轴交于A、B（3，0）两点，与y轴交于点C（0，－3），抛物线的顶点为D．

(1)、求抛物线的解析式；

(2)、点P在抛物线的对称轴上，点Q在x轴上，若以点P、Q、B、C为顶点，BC为边的四边形为平行四边形，请直接写出点P、Q的坐标；

(3)、已知点M是x轴上的动点，过点M作x的垂线交抛物线于点G，是否存在这样的点M，使得以点A、M、G为顶点的三角形与△BCD相似，若存在，请求出点M的坐标；若不存在，请说明理由．

查看试题解析