山东省济宁市兖州区2022年中考二模数学试题

试卷更新日期：2022-05-31 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列四个实数中，最大的实数是（）

A、 $| - 2 |$ B、-1 C、0 D、 $\sqrt{2}$

查看试题解析
2. 在攻击人类的病毒中，某类新型冠状病毒体积较大，直径约为0.0000000125米，含约3万个碱基，拥有RNA病毒中最大的基因组，比艾滋病毒和丙型肝炎的基因组大三倍以上，比流感的基因组大两倍.0.0000000125用科学记数法表示为（）

A、 $12.5 \times 1 0^{- 9}$ B、 $0.125 \times 1 0^{- 7}$ C、 $1.25 \times 1 0^{- 7}$ D、 $1.25 \times 1 0^{- 8}$

查看试题解析
3. 一副直角三角尺如图摆放，点D在 $B C$ 的延长线上， $E F / / B C$ ， $∠ B = ∠ E D F = 90 °$ ， $∠ A = 30 °$ ， $∠ F = 45 °$ ，则∠ $C E D$ 的度数是（）

A、 $15 °$ B、 $25 °$ C、 $45 °$ D、 $60 °$

查看试题解析
4. 如图是由6个大小相同的立方体组成的几何体，在这个几何体的三视图中，是中心对称图形的是 $($ 　　 $)$

A、主视图 B、左视图 C、俯视图 D、主视图和左视图

查看试题解析
5. 以下问题，不适合用全面调查的是（）

A、旅客上飞机前的安检 B、公司招聘总经理助理，对应聘人员的面试 C、了解某校七年级学生阳光体育运动时间 D、了解一批灯泡的使用寿命

查看试题解析
6. 下列运算正确的是（）

A、 $\sqrt{4} = \pm 2$ B、 $a^{3} \div a^{2} = a$ C、 $m^{2} \cdot m^{3} = m^{6}$ D、 ${(2 x^{2})}^{3} = 6 x^{6}$

查看试题解析
7. 《九章算术》中有一题：“今有二人同所立，甲行率七，乙行率三，乙东行，甲南行十而斜东北与乙会．问甲、乙行各几何？”大意是说：已知甲、乙二人同时从同一地点出发，甲的速度为7，乙的速度为3．乙一直向东走，甲先向南走10，后又向东北方向走了一段后与乙相遇．那么相遇时，甲、乙各走了多少？设甲、乙二人从出发到相遇的时间为x，根据题意，可列方程正确的是（）

A、 $(3 x)^{2} + (7 x)^{2} = 1 0^{2}$ B、 $(3 x)^{2} + 1 0^{2} = (7 x)^{2}$ C、 $(3 x)^{2} + 1 0^{2} = (7 x - 10)^{2}$ D、 $(3 x + 10)^{2} + 1 0^{2} = (7 x)^{2}$

查看试题解析
8. 欧几里得的《原本》记载，形如 $x^{2} + a x = b^{2}$ 的方程的图解法是：画 $R t Δ A B C$ ，使 $∠ A C B = 9 0^{∘}$ ， $B C = \frac{a}{2}$ ， $A C = b$ ，再在斜边 $A B$ 上截取 $B D = \frac{a}{2}$ .则该方程的一个正根是（）

A、 $A C$ 的长 B、 $A D$ 的长 C、 $B C$ 的长 D、 $C D$ 的长

查看试题解析
9. 如图，AB为⊙O的直径，点P在AB的延长线上，PC，PD与⊙O相切，切点分别为C，D．若AB＝6，PC＝4，则sin∠CAD等于（　　）

A、 $\frac{3}{5}$ B、 $\frac{2}{3}$ C、 $\frac{3}{4}$ D、 $\frac{4}{5}$

查看试题解析
10. 如图是二次函数y=ax²+bx+c（a≠0）的图像的一部分，给出下列命题：①abc＞0；②b=-a；③9a-3b+c=0；④m（am+b）≥a-b（m为任意实数）；⑤4ac-b²＜0，其中正确的命题有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 使 $\sqrt{x - 1}$ 有意义的x的取值范围是．

查看试题解析
12. 已知点P（a+3，7+a）位于二、四象限的角平分线上，则点P的坐标为.

查看试题解析
13. 如图，已知 $∠ B A C = 60 °$ ， $A D$ 是角平分线且 $A D = 10$ ，作 $A D$ 的垂直平分线交 $A C$ 于点F，作 $D E ⊥ A C$ ，则 $△ D E F$ 周长为．

查看试题解析
14. 如图，在矩形 $A B C D$ 中，点 $E ， F$ 分别在 $B C ， A D$ 上， $A F = E C$ ．只需添加一个条件即可证明四边形 $A E C F$ 是菱形，这个条件可以是（写出一个即可）．

查看试题解析
15. 如图，抛物线 $y = a x^{2} + c$ 与直线 $y = m x + n$ 交于 $A (- 1 ， p) ， B (2 ， q)$ 两点，则不等式 $a x^{2} + m x + c > n$ 的解集是．

查看试题解析

三、解答题

16. 先化简，再求值： $\frac{x + 1}{x^{2} - 4} \cdot (\frac{1}{x + 1} + 1)$ ，其中x为不等式组 ${\begin{array}{l} x + 1 \geq 0 \\ 5 - 2 x > 3 \end{array}$ 的整数解．

查看试题解析
17. 网络技术的发展对学生学习方式产生巨大的影响，某校为了解学生每周课余利用网络资源进行自主学习的时间，在本校随机抽取若干名学生进行问卷调查，现将调查结果绘制成如下不完整的统计图表，请根据图表中的信息解答下列问题
组别
学习时间x（h）
频数（人数）
A
0＜x≤1
8
B
1＜x≤2
24
C
2＜x≤3
32
D
3＜x≤4
n
E
4小时以上
4

(1)、表中的n= ，中位数落在组，扇形统计图中B组对应的圆心角为°；

(2)、请补全频数分布直方图；

(3)、该校准备召开利用网络资源进行自主学习的交流会，计划在E组学生中随机选出两人进行经验介绍，已知E组的四名学生中，七、八年级各有1人，九年级有2人，请用画树状图法或列表法求抽取的两名学生都来自九年级的概率．

查看试题解析
18. 如图1是安装在斜屋面上的热水器，图2是安装该热水器的侧面示意图．已知斜屋面的倾斜角为25°，长度为2.1米的真空管AB与水平线AD的夹角为40°，安装热水器的铁架水平管BC长0.2米，（sin40°≈06428，cos40°≈0.7660，tan40°≈0.8391，sin25°≈0.4226，cos25°≈0.9063，tan25°≈0.4663）求：

(1)、真空管上端B到AD的距离（结果精确到0.01米）．

(2)、铁架垂直管CE的长度（结果精确到0.01米）．

查看试题解析
19. 如图，在平面直角坐标系 $x O y$ 中，一次函数 $y = \frac{1}{2} x + b$ 的图像分别与x轴、y轴交于点A、B，与反比例函数 $y = \frac{k}{x} (x > 0)$ 的图像交于点C，连接 $O C$ ．已知点 $A (- 4 ， 0)$ ， $A B = 2 B C$ ．

(1)、求b、k的值；

(2)、求 $△ A O C$ 的面积．

查看试题解析
20. 如图，四边形 $A B C D$ 内接于 $⊙ O$ ， $A C$ 是 $⊙ O$ 的直径， $A C$ 与 $B D$ 交于点E， $P B$ 切 $⊙ O$ 于点B．

(1)、求证： $∠ P B A = ∠ O B C$ ；

(2)、若 $∠ P B A = 20 °$ ， $∠ A C D = 40 °$ ，求证： $△ O A B ∽ △ C D E$ ．

查看试题解析
21. 在平面直角坐标系 $x O y$ 中， $⊙ O$ 的半径为1，对于点A和线段 $B C$ ，给出如下定义：若将线段 $B C$ 绕点A旋转可以得到 $⊙ O$ 的弦 $B^{'} C^{'}$ （ $B^{'} ， C^{'}$ 分别是 $B ， C$ 的对应点），则称线段 $B C$ 是 $⊙ O$ 的以点A为中心的“关联线段”．

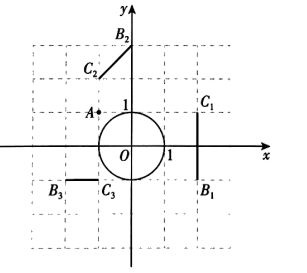(1)、如图，点 $A ， B_{1} ， C_{1} ， B_{2} ， C_{2} ， B_{3} ， C_{3}$ 的横､纵坐标都是整数．在线段 $B_{1} C_{1} ， B_{2} C_{2} ， B_{3} C_{3}$ 中， $⊙ O$ 的以点A为中心的“关联线段”是；

(2)、 $△ A B C$ 是边长为1的等边三角形，点 $A (0 ， t)$ ，其中 $t \neq 0$ ．若 $B C$ 是 $⊙ O$ 的以点A为中心的“关联线段”，求t的值；

(3)、在 $△ A B C$ 中， $A B = 1 ， A C = 2$ ．若 $B C$ 是 $⊙ O$ 的以点A为中心的“关联线段”，直接写出 $O A$ 的最小值和最大值，以及相应的 $B C$ 长．

查看试题解析
22. 如图，在平面直角坐标系中，二次函数y＝ $\frac{1}{4}$ x²＋bx＋c的图象与x轴交于点A（﹣3，0）和点B（5，0），顶点为点D，动点M、Q在x轴上（点M在点Q的左侧），在x轴下方作矩形MNPQ，其中MQ＝3，MN＝2．矩形MNPQ沿x轴以每秒1个单位长度的速度向右匀速运动，运动开始时，点M的坐标为（﹣6，0），当点M与点B重合时停止运动，设运动的时间为t秒（t＞0）．

(1)、b＝， c＝．

(2)、连接BD，求直线BD的函数表达式．

(3)、在矩形MNPQ运动的过程中，MN所在直线与该二次函数的图象交于点G，PQ所在直线与直线BD交于点H，是否存在某一时刻，使得以G、M、H、Q为顶点的四边形是面积小于10的平行四边形？若存在，求出t的值；若不存在，请说明理由．

(4)、连接PD，过点P作PD的垂线交y轴于点R，直接写出在矩形MNPQ整个运动过程中点R运动的路径长．

查看试题解析

组别	学习时间x（h）	频数（人数）
A	0＜x≤1	8
B	1＜x≤2	24
C	2＜x≤3	32
D	3＜x≤4	n
E	4小时以上	4