山东省济宁市泗水县2022年九年级中考二模数学试题

试卷更新日期：2022-05-31 类型：中考模拟

进入出卷网下载

一、单选题

1. 2022的相反数是（）

A、2022 B、 $- 2202$ C、 $- \frac{1}{2022}$ D、 $- 2022$

查看试题解析
2. 下列图形中既是中心对称图形又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列计算正确的是（）

A、 ${(a b^{4})}^{2} = a b^{8}$ B、 $3 x + 3 y = 6 x y$ C、 $b^{6} \div b^{3} = b^{2}$ D、 $3 a b \cdot 2 a = 6 a^{2} b$

查看试题解析
4. 如图所示的几何体是由五个小正方体搭建而成的，则左视图是（）

A、 B、 C、 D、

查看试题解析
5. 4月22日是世界地球日，保护生态环境是我们的责任．据科学家估计，地球的年龄大约是4550000000年，将4550000000用科学记数法表示为（）

A、 $4.55 \times 1 0^{10}$ B、 $4.55 \times 1 0^{9}$ C、 $4.55 \times 1 0^{8}$ D、 $4.55 \times 1 0^{7}$

查看试题解析
6. 一组数据：1，3，3，3，5，若去掉一个数据3，则下列统计量中发生变化的是（）

A、众数 B、中位数 C、平均数 D、方差

查看试题解析
7. 疫情期间，某快递公司推出无接触配送服务，4月份第1周接到1.5万件订单，前3周共接到4.8万件订单，设第1周到第3周订单的周平均增长率为x，则可列方程为（）

A、 $1.5 (1 + 2 x) = 4.8$ B、 $1.5 \times 2 (1 + x) = 4.8$ C、 $1.5 (1 + x)^{2} = 4.8$ D、 $1.5 + 1.5 (1 + x) + 1.5 (1 + x)^{2} = 4.8$

查看试题解析
8. 在平面直角坐标系中，函数 $y = \frac{2}{x} (x > 0)$ 与 $y = - x + 4$ 的图象交于点 $P (a ， b)$ 则代数式 $\frac{1}{a} + \frac{1}{b}$ 的值是（）

A、4 B、3 C、2 D、1

查看试题解析
9. 如图，在 $R t △ B A D$ 中，延长斜边 $B D$ 到点C，使 $D C = \frac{1}{2} B D$ ，连接 $A C$ ，若 $t a n ∠ A D B = \frac{3}{4}$ ，则 $t a n ∠ C A D$ 的值（）

A、 $\frac{\sqrt{3}}{4}$ B、 $\frac{1}{4}$ C、 $\frac{\sqrt{3}}{3}$ D、 $\frac{1}{3}$

查看试题解析
10. 已知 $y = \sqrt{(x - 3)^{2}} - x + 4$ ，当x分别取正整数1，2，3，4，5，…，2022时，所对应y值的总和是（）

A、2026 B、2027 C、2028 D、2029

查看试题解析

二、填空题

11. 如图，已知平行线a，b，一个直角三角板的直角顶点在直线a上，另一个顶点在直线b上，若 $∠ 1 = 70 °$ ，则 $∠ 2$ 的度数为．

查看试题解析
12. 因式分解： ${xy}^{2} + 2 xy + x =$ ．

查看试题解析
13. 如图，正五边形 $A B C D E$ 内接于 $⊙ O$ ，且 $⊙ O$ 的半径为5，则弧 $A B$ 的长为（结果保留 $π$ ）．

查看试题解析
14. 如图，在平面直角坐标系中，边长为5的正方形ABCD斜靠在y轴上，顶点 $A (3 ， 0)$ ，反比例函数 $y = \frac{k}{x}$ 图象经过点C，将正方形ABCD绕点A顺时针旋转一定角度后，得正方形 $A B_{1} C_{1} D_{1}$ ，且 $B_{1}$ 恰好落在X轴的正半轴上，此时边 $B_{1} C_{1}$ 交反比例图象于点E，则点E的纵坐标是．

查看试题解析
15.
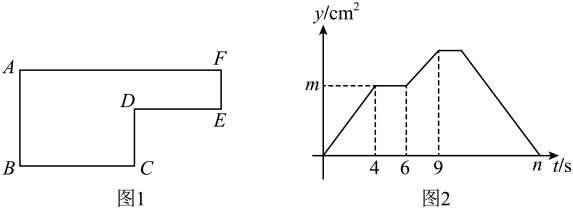
如图1，动点P以 $2 c m / s$ 的速度沿图1中多边形（ $∠ A = ∠ B = ∠ C = ∠ D = ∠ E = ∠ F = 90 °$ ）的边运动，运动路径为： $B \to C \to D \to E \to F \to A$ ，相应的 $△ A B P$ 的面积y（单位： $c m^{2}$ ）关于运动时间t（单位：s）的函数图象如图2，若 $A B = 6$ ，有下列结论：①图1中 $B C$ 的长是 $8 c m$ ；②图2中m的值是 $24 c m^{2}$ ；③图1中多边形所围成图形的面积是 $60 c m^{2}$ ；④图2中n的值是17．其中正确的是．（只填序号）

查看试题解析

三、解答题

16. 解方程： $\frac{2 x}{x - 2} = 1 - \frac{3}{2 - x}$

查看试题解析
17. 某学校在“强国有我”演讲比赛中，对优秀选手的综合分数进行分组统计，结果如表所示：
组号
分组
频数
频率
一
$6 \leq m < 7$
2
0.1
二
$7 \leq m < 8$
7
b
三
$8 \leq m < 9$
a
0.5
四
$9 \leq m \leq 10$
2
0.1

(1)、a的值是， b的值是；

(2)、若用扇形图来描述，分组在 $6 \leq m < 7$ 内所对应的扇形图的圆心角大小是；

(3)、将在第一组内的两名选手记为： $A_{1}$ 、 $A_{2}$ ，在第四组内的两名选手记为： $B_{1}$ 、 $B_{2}$ ，从第一组和第四组中随机选取2名选手进行调研座谈，求第一组至少有1名选手被选中的概率（用树状图或列表法列出所有可能结果）．

查看试题解析
18. 如图，在 $△ A B C$ 中， $∠ B A C = 90 ° ， B D$ 平分 $∠ A B C$ ．

(1)、求作 $△ C D E$ 使点E在 $B C$ 上，且 $△ C D E ∽ △ C B D$ ；（要求：尺规作图，保留作图痕迹，不写作法）

(2)、在（1）的条件下，若 $B A = \sqrt{3} ， ∠ A B C = 60 °$ ，求 $C E$ 长．

查看试题解析
19. 某中学开学初到商场购买A.B两种品牌的足球，购买A种品牌的足球50个，B种品牌的足球25个，共花费4500元.已知购买一个B种品牌的足球比购买一个A种品牌的足球多花30元

(1)、求购买一个A种品牌、一个B种品牌的足球各需多少元?

(2)、学校为了响应习总书记“足球进校园”的号召，决定再次购进A.B两种品牌足球共50个，正好赶上商场对商品价格进行调整，A品牌足球售价比第一次购买时提高4元，B品牌足球按第一次购买时售价的9折出售，如果学校此次购买A.B两种品牌足球的总费用不超过第一次花费的70%，且保证这次购买的B种品牌足球不少于23个，则这次学校有哪几种购买方案?

查看试题解析
20. 如图，在半径为5cm的 $⊙ O$ 中，AB是 $⊙ O$ 的直径，CD是过 $⊙ O$ 上点C的直线，且 $A D ⊥ D C$ 于点D，AC平分 $∠ B A D$ ， E是BC的中点， $O E = 3 c m$ ．

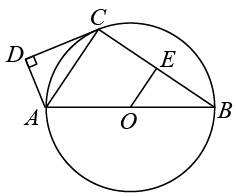(1)、求证：CD是 $⊙ O$ 的切线；

(2)、求AD的长，

查看试题解析
21. 阅读理解：对于任意正实数a，b，
∵ $(\sqrt{a} - \sqrt{b})^{2} \geq 0$ ，
∴ $a - 2 \sqrt{a b} + b \geq 0$ ，
∴ $a + b \geq 2 \sqrt{a b}$ ，
∴当 $a = b$ 时， $a + b$ 有最小值 $2 \sqrt{a b}$ ．
根据上述内容，回答下列问题

(1)、若 $m > 0$ ，只有当 $m =$ 时， $m + \frac{1}{m}$ 有最小值；若 $m > 0$ ，只有当 $m =$ 时， $2 m + \frac{8}{m}$ 有最小值；

(2)、疫情需要为解决临时隔离问题，检测人员利用一面墙（墙的长度不限）和63米长的钢丝网围成了9间相同的矩形隔离房，如图设每间隔离房的面积为S（米 $^{2}$ ）．问：当每间隔离房的长宽各为多少时，使每间隔离房面积S最大？最大面积是多少？

查看试题解析
22. 如图，在矩形 $A B C O$ 中，点O为坐标原点，点B的坐标为 $(4 ， 3)$ ，点A、C在坐标轴上，点D在 $B C$ 边上，直线 $l ： y = 2 x - 3$ ．

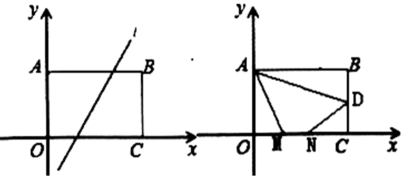(1)、分别求直线l与边 $A B$ 、边 $O C$ 的交点坐标；

(2)、当点D为 $B C$ 边的中点时，点M，N为 $O C$ 边上两个动点且 $M N = 1$ ，求四边形 $A D N M$ 周长的最小值；

(3)、已知点E在第一象限，且是直线l上的点，若 $△ A D E$ 是等腰直角三角形，直接写出点E的坐标；

查看试题解析

组号	分组	频数	频率
一	$6 \leq m < 7$	2	0.1
二	$7 \leq m < 8$	7	b
三	$8 \leq m < 9$	a	0.5
四	$9 \leq m \leq 10$	2	0.1