山东省济南市长清区2022年中考二模数学试题

试卷更新日期：2022-05-31 类型：中考模拟

进入出卷网下载

一、单选题

1. －2的相反数是（）

A、 $\pm$ 2 B、2 C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
2. 图中立体图形的俯视图是(　　)

A、 B、 C、 D、

查看试题解析
3. 南沙新区的面积为80 300 000平方米，用科学记数法可表示为（）平方米．

A、 $8.03 \times 1 0^{4}$ B、 $8.03 \times 1 0^{5}$ C、 $8.03 \times 1 0^{6}$ D、 $8.03 \times 1 0^{7}$

查看试题解析
4. 如图，直线AB∥ CD，∠ B=50°，∠ C=40°，则∠E等于（　　）

A、70° B、80° C、90° D、100°

查看试题解析
5. 2017年12月15日，北京2022年冬奥会会徽“冬梦”正式发布. 以下是参选的会徽设计的一部分图形，其中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
6. 实数a，b在数轴上对应点的位置如图所示，则下列结论正确的是（）

A、 $a + b > 0$ B、 $a - b > 0$ C、 $a b > 0$ D、 $| a | > | b |$

查看试题解析
7. 化简 $\frac{a^{2}}{a - b} - \frac{b^{2}}{a - b}$ 的结果为（）

A、 $a - b$ B、 $a + b$ C、 $\frac{a + b}{a - b}$ D、 $\frac{a - b}{a + b}$

查看试题解析
8. 在一个不透明纸箱中放有除了数字不同外，其它完全相同2张卡片，分别标有数字1、2，从中任意摸出一张，放回搅匀后再任意摸出一张，两次摸出的数字之和为奇数的概率为（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{3}{4}$

查看试题解析
9. 函数 $y = a x + a$ 与 $y = \frac{a}{x} (a \neq 0)$ 在同一平面直角坐标系中的图象可能是（）

A、 B、 C、 D、

查看试题解析
10. 如图，活动课小明利用一个锐角是30°的三角板测量一棵树的高度，已知他与树之间的水平距离BE为9m，AB为1.5m（即小明的眼睛距地面的距离），那么这棵树高是（　　）

A、3 $\sqrt{3}$ m B、27 $\sqrt{3}$ m C、 $(3 \sqrt{3} + \frac{3}{2})$ m D、 $(27 \sqrt{3} + \frac{3}{2})$ m

查看试题解析
11. 如图，在Rt△ABC中，∠C=90°，以顶点A为圆心，适当长为半径画弧，分别交边AC、AB于点M、N，再分别以点M、N为圆心，大于 $\frac{1}{2}$ MN的长为半径画弧，两弧交于点P，作射线AP交边BC于点D，若CD=2，AB=6，则△ABD的面积是（）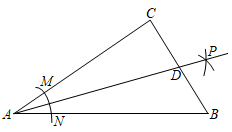

A、3 B、6 C、12 D、18

查看试题解析
12. 二次函数 $y = a x^{2} - 6 a x - 5 (a \neq 0)$ ，当 $5 \leq x \leq 6$ 时，对应的y的整数值有4个，则a的取值范围是（）

A、 $\frac{3}{5} \leq a < \frac{4}{5}$ B、 $- \frac{4}{5} \leq a < - \frac{3}{5}$ C、 $\frac{3}{5} < a \leq \frac{4}{5}$ 或 $- \frac{4}{5} \leq a < - \frac{3}{5}$ D、 $\frac{3}{5} \leq a < \frac{4}{5}$ 或 $- \frac{4}{5} < a \leq - \frac{3}{5}$

查看试题解析

二、填空题

13. 因式分解： $x^{2} - 3 x =$ .

查看试题解析
14. 一个小球在如图所示的地板上自由滚动，并随机停在某块方砖上，如果每一块方砖除颜色外完全相同，那么小球最终停留在黑砖上的概率是．

查看试题解析
15. 小明发现交通指示牌中“停车让行标志”可以看成是正八边形，如图所示，则 $∠ 1 =$ °.

查看试题解析
16. 已知方程 $x^{2} - 4 x + k = 0$ 的一个根是 $x_{1} = - 1$ ，则方程的另一根 $x_{2} =$ .

查看试题解析
17. A，B两地相距100千米，甲、乙两人骑车同时分别从A，B两地相向而行．假设他们都保持匀速行驶，则他们各自到A地的距离S（千米）都是骑车时间t（时）的一次函数．如图，直线 $l_{1}$ 、 $l_{2}$ 分别表示甲、乙骑车S与t之间关系的图象．结合图象提供的信息，经过小时两人相遇．

查看试题解析
18. 如图，矩形OABC的边OC在y轴上，边OA在x轴上，C点坐标为（0，3），点D是线段OA上的一个动点，连结CD，以CD为边作矩形CDEF，使边EF过点B．连结OF，当点D与点A重合时，所作矩形CDEF的面积为12．在点D的运动过程中，当线段OF有最大值时，则点F的坐标为．

查看试题解析

三、解答题

19. 计算： ${(\frac{1}{2})}^{- 1} - \tan 60 ° + {(\sqrt{5} - 1)}^{0} + | \sqrt{3} |$ ；

查看试题解析
20. 解不等式组： ${\begin{array}{l} 5 x - 3 \leq 2 x + 9 \\ 2 + 3 x > \frac{x + 9}{2} \end{array}$ ，并把其解集在数轴上表示出来．

查看试题解析
21. 已知，如图：在矩形ABCD中，点M、N在边AD上，且AM=DN，求证：BN=CM．

查看试题解析
22. 央视“经典咏流传”开播以来受到社会广泛关注．我市某校就“中华文化我传承——地方戏曲进校园”的喜爱情况进行了随机调查，对收集的信息进行统计，绘制了下面两幅尚不完整的统计图．请你根据统计图所提供的信息解答下列问题：图中A表示“很喜欢”，B表示“喜欢”，C表示“一般”，D表示“不喜欢”．

(1)、被调查的总人数是人；

(2)、补全条形统计图；

(3)、扇形统计图中，B部分对应的扇形圆心角是度；

(4)、若该校共有学生 $1800$ 人，请根据上述调查结果，估计该校学生中C类有多少人？

查看试题解析
23. 如图， $⊙ O$ 是 $△ A B C$ 的外接圆，其切线AE与直径BD的延长线相交于点E，且 $∠ A C B = 60 °$ ．

(1)、求证： $A E = A B$ ；

(2)、若 $D E = 2$ ，求 $⊙ O$ 的半径．

查看试题解析
24. 第24届冬季奥林匹克运动会将于2022年02月04日至2022年02月20日在中华人民共和国北京市和张家口市联合举行，这是中国历史上第一次举办冬季奥运会．冬奥会吉祥物“冰墩墩”和“雪容融”陶制品分为小套装和大套装两种．已知购买2个小套装和购买1个大套装，共需220元；购买3个小套装和2个大套装，共需390元．

(1)、求这两种套装的单价分别为多少元？

(2)、太原市某校计划用不多于1350元的资金购买这种陶制品小套装和大套装共20个作为奖品，则该校最多可以购买大套装多少个？

查看试题解析
25. 如图，已知直线 $y = \frac{1}{2} x$ 与双曲线 $y = \frac{k}{x} (k > 0)$ 交于A，B两点，且点A的横坐标为4．

(1)、求k的值；

(2)、根据图象，写出使一次函数值大于反比例函数值的x的取值范围；

(3)、若双曲线 $y = \frac{k}{x} (k > 0)$ 上一点C的纵坐标为8，求 $△ A O C$ 的面积．

查看试题解析
26.

(1)、问题发现：如图（1），在△OAB和△OCD中，OA＝OB，OC＝OD，∠AOB＝∠COD＝36°，连接AC，BD交于点M．① $\frac{A C}{B D}$ 的值为；②∠AMB的度数为；

(2)、类比探究：如图（2），在△OAB和△OCD中，∠AOB＝∠COD＝90°，∠OAB＝∠OCD＝30°，连接AC，交BD的延长线于点M．请计算 $\frac{A C}{B D}$ 的值及∠AMB的度数．

(3)、拓展延伸：在（2）的条件下，将△OCD绕点O在平面内旋转，AC，BD所在直线交于点M．若OD＝1，OB＝ $\sqrt{13}$ ，请直接写出当点C与点M重合时AC的长．

查看试题解析
27. 如图，已知抛物线 $y = - x^{2} + m x + 3$ 与x轴交于A、B两点，与y轴交于点C，点B的坐标为 $(3 ， 0)$ ．

(1)、求m的值及抛物线的顶点坐标；

(2)、点P是抛物线对称轴l上的一个动点，当 $P A + P C$ 的值最小时，求点P的坐标；

(3)、设点F是抛物线上一点，其横坐标为－2，在抛物线上是否存在一点M，使得AM被直线BF平分？若存在，请求出点M的坐标；若不存在，说明理由．

查看试题解析