山东省济南市章丘区2022年中考数学一模试卷
试卷更新日期:2022-05-31 类型:中考模拟
一、单选题
-
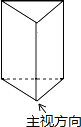
1. 的值是( )A、﹣3 B、3或﹣3 C、3 D、92. 如图,正三棱柱的主视图为( )
 A、
A、 B、
B、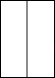 C、
C、 D、
D、 3. 银河系中大约有恒星160 000 000 000颗,数据160 000 000 000用科学记数法表示为( )A、0.16×1012 B、1.6×1011 C、16×1010 D、160×1094. 下列选项中的垃圾分类图标,属于中心对称图形的是( )A、
3. 银河系中大约有恒星160 000 000 000颗,数据160 000 000 000用科学记数法表示为( )A、0.16×1012 B、1.6×1011 C、16×1010 D、160×1094. 下列选项中的垃圾分类图标,属于中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 5. 如图所示,AE//BC,EF⊥BD,垂足为E, , 则∠2的度数为( )
5. 如图所示,AE//BC,EF⊥BD,垂足为E, , 则∠2的度数为( )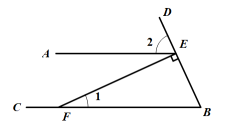 A、30° B、40° C、62° D、50°6. 下列计算正确的是( ).A、 B、 C、 D、7. 如图.AB、BC为⊙O的两条弦,连接OA、OC,点D为AB的延长线上一点,若∠CBD=62°,则∠AOC的度数为( )
A、30° B、40° C、62° D、50°6. 下列计算正确的是( ).A、 B、 C、 D、7. 如图.AB、BC为⊙O的两条弦,连接OA、OC,点D为AB的延长线上一点,若∠CBD=62°,则∠AOC的度数为( )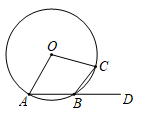 A、130° B、124° C、114° D、100°8. 为了落实“作业、睡眠、手机、读物、体质”等五项管理要求,了解学生的睡眠状况,调查了一个班50名学生每天的睡眠时间,绘成睡眠时间频数分布直方图如图所示,则所调查学生睡眠时间的众数,中位数分别为( )
A、130° B、124° C、114° D、100°8. 为了落实“作业、睡眠、手机、读物、体质”等五项管理要求,了解学生的睡眠状况,调查了一个班50名学生每天的睡眠时间,绘成睡眠时间频数分布直方图如图所示,则所调查学生睡眠时间的众数,中位数分别为( )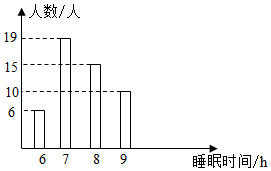 A、7h , 7h B、8h , 7.5h C、7h , 7.5h D、8h , 8h9. 正比例函数y=kx的图象经过一、三象限,则一次函数y=﹣kx+k的图象大致是( )A、
A、7h , 7h B、8h , 7.5h C、7h , 7.5h D、8h , 8h9. 正比例函数y=kx的图象经过一、三象限,则一次函数y=﹣kx+k的图象大致是( )A、 B、
B、 C、
C、 D、
D、 10. 如图,在中, , 以顶点A为圆心,适当长为半径画弧,分别交 , 于点M,N,再分别以点M,N为圆心,大于的长为半径画弧,两弧交于点P,作射线交边于点D,点E在上.若 , , , 当最小时,的面积是( )
10. 如图,在中, , 以顶点A为圆心,适当长为半径画弧,分别交 , 于点M,N,再分别以点M,N为圆心,大于的长为半径画弧,两弧交于点P,作射线交边于点D,点E在上.若 , , , 当最小时,的面积是( ) A、2 B、1 C、6 D、711. 在数学实践活动课上,某兴趣小组测量操场上篮球筐距地面的高度如图所示,已知篮球筐的直径AB 约为0.45m,某同学站在C处,先仰望篮球筐直径的一端A处,测得仰角为42°,再调整视线,测得篮球筐直径的另一端B处的仰角为35°.若该同学的目高OC为1.7m,则篮球筐距地面的高度AD大约是( )m.(结果精确到1m).(参考数据:tan42°≈0.9,tan35°=0.7,tan48°≈1.1,tan55°≈1.4)
A、2 B、1 C、6 D、711. 在数学实践活动课上,某兴趣小组测量操场上篮球筐距地面的高度如图所示,已知篮球筐的直径AB 约为0.45m,某同学站在C处,先仰望篮球筐直径的一端A处,测得仰角为42°,再调整视线,测得篮球筐直径的另一端B处的仰角为35°.若该同学的目高OC为1.7m,则篮球筐距地面的高度AD大约是( )m.(结果精确到1m).(参考数据:tan42°≈0.9,tan35°=0.7,tan48°≈1.1,tan55°≈1.4) A、2.5 B、2.6 C、2.8 D、312. 已知函数 在 上的最大值是1,最小值是 ,则 的取值范围是( )A、 B、 C、 D、
A、2.5 B、2.6 C、2.8 D、312. 已知函数 在 上的最大值是1,最小值是 ,则 的取值范围是( )A、 B、 C、 D、二、填空题
-
13. 分解因式: =.14. 在一个不透明的袋中装有6个只有颜色不同的球,其中3个红球、2个黄球和1个白球.从袋中随机摸出一个球,是黄球的概率为.15. 若关于x的一元二次方程x2+kx﹣2=0的一个根为x=1,则这个一元二次方程的另一个根为 .16. 如图,从一块直径为2cm的圆形铁皮上剪出一圆心角为90°的扇形,则此扇形的面积为cm2 .
 17. 如图,将一个装有水的杯子倾斜放置在水平的桌面上,其截面可看作一个宽BC=6厘米,长CD=16厘米的矩形.当水面触到杯口边缘时,边CD恰有一半露出水面,那么此时水面高度是厘米.
17. 如图,将一个装有水的杯子倾斜放置在水平的桌面上,其截面可看作一个宽BC=6厘米,长CD=16厘米的矩形.当水面触到杯口边缘时,边CD恰有一半露出水面,那么此时水面高度是厘米.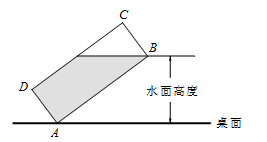 18. 如图,在矩形中, , , 点E、F分别是边、上的动点,且 , 点G是的中点,、 , 则四边形面积的最小值为 .
18. 如图,在矩形中, , , 点E、F分别是边、上的动点,且 , 点G是的中点,、 , 则四边形面积的最小值为 .
三、解答题
-
19. 计算:20. 解方程:.21. 如图,点E,F分别在菱形ABCD的边BC,CD上,且∠BAE=∠DAF.求证:AE=AF.
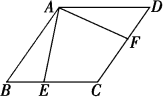 22. 达州市某中学举行了“中国梦,中国好少年”演讲比赛,菲菲同学将选手成绩划分为A、B、C、D四个等级,绘制了两种不完整统计图.
22. 达州市某中学举行了“中国梦,中国好少年”演讲比赛,菲菲同学将选手成绩划分为A、B、C、D四个等级,绘制了两种不完整统计图.
根据图中提供的信息,解答下列问题:
(1)、参加演讲比赛的学生共有人,扇形统计图中m= , n= , 并把条形统计图补充完整 .(2)、学校欲从A等级2名男生2名女生中随机选取两人,参加达州市举办的演讲比赛,请利用列表法或树状图,求A等级中一男一女参加比赛的概率.(男生分别用代码 A1、A2表示,女生分别用代码B1、B2表示)23. 如图,为的外接圆,为直径,的角平分线交于点D,过点D作的切线 , 交的延长线于点E.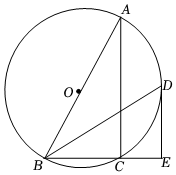 (1)、求证:;(2)、若 , , 求的半径.24. 为响应市政府“创建国家森林城市”的号召,某小区计划购进A、B两种树苗共17棵,已知A种树苗每棵80元,B种树苗每棵60元.(1)、若购进A、B两种树苗刚好用去1220元,问购进A、B两种树苗各多少棵?(2)、若购买B种树苗的数量少于A种树苗的数量,请你给出一种费用最省的方案,并求出该方案所需费用.25. 如图1,四边形为正方形,点A在y轴上,点B在x轴上,且 , , 反比例函数在第一象限的图象经过正方形的顶点C.
(1)、求证:;(2)、若 , , 求的半径.24. 为响应市政府“创建国家森林城市”的号召,某小区计划购进A、B两种树苗共17棵,已知A种树苗每棵80元,B种树苗每棵60元.(1)、若购进A、B两种树苗刚好用去1220元,问购进A、B两种树苗各多少棵?(2)、若购买B种树苗的数量少于A种树苗的数量,请你给出一种费用最省的方案,并求出该方案所需费用.25. 如图1,四边形为正方形,点A在y轴上,点B在x轴上,且 , , 反比例函数在第一象限的图象经过正方形的顶点C. (1)、求点C的坐标和反比例函数的关系式;(2)、如图 , 将正方形沿x轴向右平移m个单位长度得到正方形 , 点恰好落在反比例函数的图象上,求n值.(3)、在(2)的条件下,坐标系内是否存在点P,使以点O, , , P为顶点的四边形为平行四边形,若存在,请直接写出点P的坐标,若不存在,请说明理由.26. 图形的旋转变换是研究数学相关问题的重要手段之一,在研究三角形的旋转过程中,发现下列问题:如图 , 在中, , , 分别为、边上一点,连接 , 且 , 将绕点B在平面内旋转.
(1)、求点C的坐标和反比例函数的关系式;(2)、如图 , 将正方形沿x轴向右平移m个单位长度得到正方形 , 点恰好落在反比例函数的图象上,求n值.(3)、在(2)的条件下,坐标系内是否存在点P,使以点O, , , P为顶点的四边形为平行四边形,若存在,请直接写出点P的坐标,若不存在,请说明理由.26. 图形的旋转变换是研究数学相关问题的重要手段之一,在研究三角形的旋转过程中,发现下列问题:如图 , 在中, , , 分别为、边上一点,连接 , 且 , 将绕点B在平面内旋转. (1)、观察猜想
(1)、观察猜想绕点B旋转到如图2所示的位置,若 , 则的值为 .
(2)、类比探究若 , 将绕点B旋转到如图3所示的位置,求的值.
(3)、拓展应用若 , M为的中点, , 当时,请直接写出的值.
27. 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线 , 且抛物线经过B(1,0),C(0,3)两点,与x轴交于点A.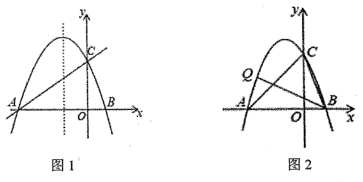 (1)、求抛物线的解析式;(2)、如图1,在抛物线的对称轴直线上找一点M,使点M到点B的距离与到点C的距离之和最小,求出点M的坐标;(3)、如图2,点Q为直线AC上方抛物线上一点,若∠CBQ=45°,请求出点Q坐标.
(1)、求抛物线的解析式;(2)、如图1,在抛物线的对称轴直线上找一点M,使点M到点B的距离与到点C的距离之和最小,求出点M的坐标;(3)、如图2,点Q为直线AC上方抛物线上一点,若∠CBQ=45°,请求出点Q坐标.