山东省济南市市中区2022年二模数学试题
试卷更新日期:2022-05-31 类型:中考模拟
一、单选题
-
1. 的倒数是( )A、 B、 C、 D、2. 下面几何体的俯视图是( )
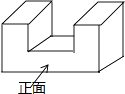 A、
A、 B、
B、 C、
C、 D、
D、 3. 2月10日,奥林匹克广播服务公司(OBS)首席执行官伊阿尼斯·埃克萨科斯在北京冬奥会每日例行新闻发布会上表示,北京冬奥会在开赛的第四天便成为了历史上收视最高的一届冬奥会,伊阿尼斯·埃克萨科斯表示,关注北京冬奥会的人群比往届都多,北京冬奥会在全球收视预计将超过2 000 000 000人次,数字2 000 000 000用科学记数法表示为( ).A、 B、 C、 D、4. 如图,直线 , 则( ).
3. 2月10日,奥林匹克广播服务公司(OBS)首席执行官伊阿尼斯·埃克萨科斯在北京冬奥会每日例行新闻发布会上表示,北京冬奥会在开赛的第四天便成为了历史上收视最高的一届冬奥会,伊阿尼斯·埃克萨科斯表示,关注北京冬奥会的人群比往届都多,北京冬奥会在全球收视预计将超过2 000 000 000人次,数字2 000 000 000用科学记数法表示为( ).A、 B、 C、 D、4. 如图,直线 , 则( ).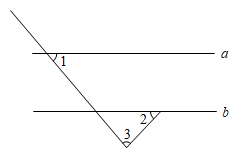 A、 B、 C、 D、5. 下列图形中,既是中心对称图形又是轴对称图形的是( )A、
A、 B、 C、 D、5. 下列图形中,既是中心对称图形又是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 6. 下列运算正确的是( )A、 B、 C、 D、7.
6. 下列运算正确的是( )A、 B、 C、 D、7.如图,边长均为1个单位的正方形组成的方格纸内有一张笑脸图案,已知左眼的坐标是(﹣1,0),那么右眼关于鼻子所在的水平线对称的点的坐标是( )
 A、(1,﹣2) B、(1,﹣1) C、(﹣1,0) D、(﹣1,﹣2)8. 2022年冬奥会古祥物为“冰墩墩”,冬残奥会吉祥物为“雪容融”.如图,现有三张正面明有吉祥物的不透明卡片,卡片除正两图案不同外,其余均相同,其中两张正面印有冰墩墩图案,一张正面印有雪容融图案,将三张卡片正面向下洗匀,从中随机仙取两张卡片,则抽出的两张都是冰墩墩卡片的概率事( )
A、(1,﹣2) B、(1,﹣1) C、(﹣1,0) D、(﹣1,﹣2)8. 2022年冬奥会古祥物为“冰墩墩”,冬残奥会吉祥物为“雪容融”.如图,现有三张正面明有吉祥物的不透明卡片,卡片除正两图案不同外,其余均相同,其中两张正面印有冰墩墩图案,一张正面印有雪容融图案,将三张卡片正面向下洗匀,从中随机仙取两张卡片,则抽出的两张都是冰墩墩卡片的概率事( ) A、 B、 C、 D、9. 已知一次函数 , 函数值y随自变量x的增大而减小,且 , 则函数的大致图象是( )A、
A、 B、 C、 D、9. 已知一次函数 , 函数值y随自变量x的增大而减小,且 , 则函数的大致图象是( )A、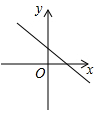 B、
B、 C、
C、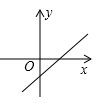 D、
D、 10. 如图,在Rt△ABC中,∠C=90°,AB=2CB=4.以点B为圆心、适当长为半径作弧,分别交BC,BA于点D,E,再分别以点D,E为圆心、大于的长为半径作弧,两弧在△ABC内部交于点F,作射线BF;分别以点A,C为圆心、大于的长为半径作弧,两弧交于G,H两点,作直线GH交BF于点J,交AB于点K,则△JKB的面积是( )
10. 如图,在Rt△ABC中,∠C=90°,AB=2CB=4.以点B为圆心、适当长为半径作弧,分别交BC,BA于点D,E,再分别以点D,E为圆心、大于的长为半径作弧,两弧在△ABC内部交于点F,作射线BF;分别以点A,C为圆心、大于的长为半径作弧,两弧交于G,H两点,作直线GH交BF于点J,交AB于点K,则△JKB的面积是( )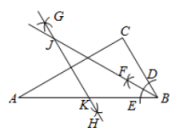 A、2 B、1 C、 D、11. 小明家的洗手盆上装有一种抬启式水龙头(如图1),完全开启后,把手AM的仰角α=37°,此时把手端点A、出水口点B和落水点C在同一直线上,洗手盆及水龙头的相关数据如图2,则线段CH长是( )(参考数据: , , )
A、2 B、1 C、 D、11. 小明家的洗手盆上装有一种抬启式水龙头(如图1),完全开启后,把手AM的仰角α=37°,此时把手端点A、出水口点B和落水点C在同一直线上,洗手盆及水龙头的相关数据如图2,则线段CH长是( )(参考数据: , , )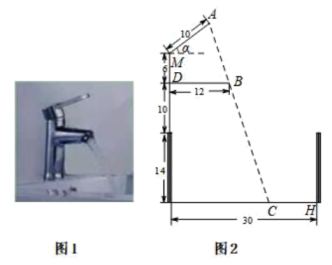 A、9 B、8 C、10 D、1112. 定义:对于已知的两个函数,任取自变量x的一个值,当x≥0时,它们对应的函数值相等;当x<0时,它们对应的函数值互为相反数,我们称这样的两个函数互为相关函数.例如:正比例函数 , 它的相关函数为 . 已知点M,N的坐标分别为 , , 连结MN,若线段MN与二次函数的相关函数的图象有两个公共点,则n的取值范围为( )A、或 B、或 C、或 D、或
A、9 B、8 C、10 D、1112. 定义:对于已知的两个函数,任取自变量x的一个值,当x≥0时,它们对应的函数值相等;当x<0时,它们对应的函数值互为相反数,我们称这样的两个函数互为相关函数.例如:正比例函数 , 它的相关函数为 . 已知点M,N的坐标分别为 , , 连结MN,若线段MN与二次函数的相关函数的图象有两个公共点,则n的取值范围为( )A、或 B、或 C、或 D、或二、填空题
-
13. 分解因式:a2-6a+9=.14. 如图,一个转盘,转盘上共有红、白两种不同的颜色,已知红色区域的圆心角为 , 自由转动转盘,指针落在白色区域的概率是.
 15. 若方程有两个相等的实数根,则m= .16. 已知 为 的直径, 为平行四边形, 与 交于点 、 ,若 ,则图中阴影部分的面积为 .
15. 若方程有两个相等的实数根,则m= .16. 已知 为 的直径, 为平行四边形, 与 交于点 、 ,若 ,则图中阴影部分的面积为 .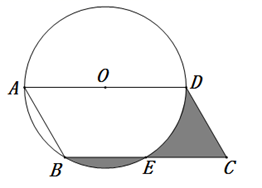 17. 把1~9这九个数填入3×3方格中,使其任意一行,任意一列及任意一条对角线上的数之和都相等,这样便构成了一个“九宫格”,它源于我国古代的“洛书”(图1),是世界上最早的“幻方”.图2是仅可以看到部分数值的“九宫格”,则的值为 .
17. 把1~9这九个数填入3×3方格中,使其任意一行,任意一列及任意一条对角线上的数之和都相等,这样便构成了一个“九宫格”,它源于我国古代的“洛书”(图1),是世界上最早的“幻方”.图2是仅可以看到部分数值的“九宫格”,则的值为 . 18. 如图,矩形纸片ABCD,AD=12,AB=4,点E在线段BC上,将△ECD沿DE向上翻折,点C的对应点C′落在线段AD上,点M,N分别是线段AD与线段BC上的点,将四边形ABNM沿MN向上翻折,点B恰好落在线段DE的中点B′处.则线段MN的长 .
18. 如图,矩形纸片ABCD,AD=12,AB=4,点E在线段BC上,将△ECD沿DE向上翻折,点C的对应点C′落在线段AD上,点M,N分别是线段AD与线段BC上的点,将四边形ABNM沿MN向上翻折,点B恰好落在线段DE的中点B′处.则线段MN的长 .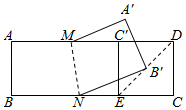
三、解答题
-
19. 计算: .20. 解不等式组 , 并写出该不等式组的整数解.21. 如图,四边形ABCD是平行四边形,E,F是对角线AC的三等分点,连接BE,DF.证明BE=DF.
 22. 某校组织了一场关于防自然灾害的知识讲座,并在讲座后进行了满分为100分的“防自然灾害知识测评”,为了了解学生的测评情况,学校在七、八年级中分别随机抽取了50名学生的分数进行整理分析,已知分数x均为整数,且分为A,B,C,D,E五个等级,分别是:A:90≤x≤100,B:80≤x<90,C:70≤x<80,D:60≤x<70,E:0≤x<60.
22. 某校组织了一场关于防自然灾害的知识讲座,并在讲座后进行了满分为100分的“防自然灾害知识测评”,为了了解学生的测评情况,学校在七、八年级中分别随机抽取了50名学生的分数进行整理分析,已知分数x均为整数,且分为A,B,C,D,E五个等级,分别是:A:90≤x≤100,B:80≤x<90,C:70≤x<80,D:60≤x<70,E:0≤x<60.并给出了部分信息:
【一】七年级D等级的学生人数占七年级抽取人数的20%,
八年级C等级中最低的10个分数分别为:
73,70,75,70,74,75,72,73,73,74
【二】两个年级学生防自然灾害知识测评分数统计图:
 (1)、请补全条形统计图;(2)、直接写出m的值为 , 八年级学生知识测评分数扇形统计图中A部分的圆心角度数为;(3)、八年级学生防自然灾害知识测评分数的中位数为 , 八年级C等级中最低的10个分数的众数为;(4)、若分数不低于80分表示该生对防自然灾害知识掌握较好,且该校七年级有1800人,请估计该校七年级所有学生中,对防自然灾害知识掌握较好的学生人数.23. 如图,已知AB为⊙O的直径,E是AB延长线上一点,点C是⊙O上的一点,连接EC、BC、AC,且EC是⊙O的切线,C为切点.
(1)、请补全条形统计图;(2)、直接写出m的值为 , 八年级学生知识测评分数扇形统计图中A部分的圆心角度数为;(3)、八年级学生防自然灾害知识测评分数的中位数为 , 八年级C等级中最低的10个分数的众数为;(4)、若分数不低于80分表示该生对防自然灾害知识掌握较好,且该校七年级有1800人,请估计该校七年级所有学生中,对防自然灾害知识掌握较好的学生人数.23. 如图,已知AB为⊙O的直径,E是AB延长线上一点,点C是⊙O上的一点,连接EC、BC、AC,且EC是⊙O的切线,C为切点.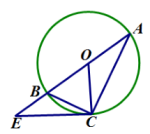 (1)、求证:∠BCE=∠A;(2)、过点A作AD垂直于直线EC于D,若AD=3,DE=4,求⊙O的半径.24. 为了保护环境,某开发区综合治理指挥部决定购买A,B两种型号的污水处理设备共10台.已知用90万元购买A型号的污水处理设备的台数与用75万元购买B型号的污水处理设备的台数相同,每台设备价格及月处理污水量如下表所示:
(1)、求证:∠BCE=∠A;(2)、过点A作AD垂直于直线EC于D,若AD=3,DE=4,求⊙O的半径.24. 为了保护环境,某开发区综合治理指挥部决定购买A,B两种型号的污水处理设备共10台.已知用90万元购买A型号的污水处理设备的台数与用75万元购买B型号的污水处理设备的台数相同,每台设备价格及月处理污水量如下表所示:污水处理设备
A型
B型
价格(万元/台)
m
m﹣3
月处理污水量(吨/台)
2200
1800
(1)、求m的值;(2)、由于受资金限制,指挥部用于购买污水处理设备的资金不超过165万元,问采用何种购买方案可以使得每月处理污水量的吨数为最多?并求出最多吨数.25. 如图,直线AC与双曲线交于A(m,6),B(3,n)两点,与x轴交于点C,直线AD与x轴交于点D(-11,0), (1)、请直接写出m,n的值;(2)、若点E在x轴上,若点F在y轴上,求的最小值;(3)、P是直线AD上一点,Q是双曲线上一点,是否存在点P,Q,使得四边形ACQP是正方形?若存在,求出点P,Q的坐标;若不存在,请说明理由.26. 如图1,在△ABC中,∠BAC=90°,AB=AC,点D在边AC上,CD⊥DE,且CD=DE,连接BE,取BE的中点F,连接DF.
(1)、请直接写出m,n的值;(2)、若点E在x轴上,若点F在y轴上,求的最小值;(3)、P是直线AD上一点,Q是双曲线上一点,是否存在点P,Q,使得四边形ACQP是正方形?若存在,求出点P,Q的坐标;若不存在,请说明理由.26. 如图1,在△ABC中,∠BAC=90°,AB=AC,点D在边AC上,CD⊥DE,且CD=DE,连接BE,取BE的中点F,连接DF.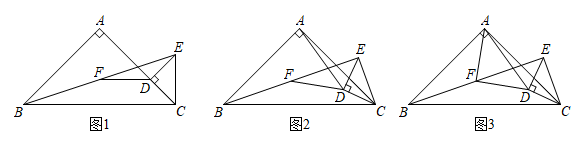 (1)、请直接写出∠ADF的度数及线段AD与DF的数量关系;(2)、将图1中的△CDE绕点C按逆时针旋转,
(1)、请直接写出∠ADF的度数及线段AD与DF的数量关系;(2)、将图1中的△CDE绕点C按逆时针旋转,①如图2,(1)中∠ADF的度数及线段AD与DF的数量关系是否仍然成立?请说明理由;
②如图3,连接AF,若AC=3,CD=1,求S△ADF的取值范围.
27. 抛物线过点A(-3,0),点B(1,0)与y轴交于点C,顶点为D,点E在y轴负半轴上.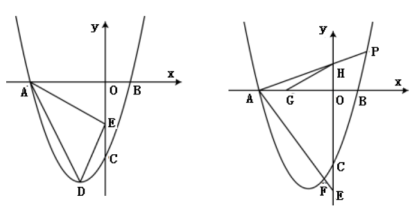 (1)、求抛物线的表达式及点D的坐标;(2)、若△ADE是直角三角形,求点E的坐标;(3)、点P是抛物线在第一象限内的点,连接AP交y轴于点H,连接AE交抛物线于点F,点G在线段OA上,且AG=CE,连接GH,若∠EAO=2∠OGH, , 求点F的坐标.
(1)、求抛物线的表达式及点D的坐标;(2)、若△ADE是直角三角形,求点E的坐标;(3)、点P是抛物线在第一象限内的点,连接AP交y轴于点H,连接AE交抛物线于点F,点G在线段OA上,且AG=CE,连接GH,若∠EAO=2∠OGH, , 求点F的坐标.