山东省济南市莱芜区2022年中考二模数学试题
试卷更新日期:2022-05-31 类型:中考模拟
一、单选题
-
1. 2022的相反数是( )A、2022 B、 C、﹣2022 D、2. 如图1是用5个相同的正方体搭成的立体图形.若由图1变化至图2,则三视图中没有发生变化的是( )
 A、俯视图 B、主视图和俯视图 C、主视图和左视图 D、左视图和俯视图3. 2022年北京冬奥会中国队运动员微博、抖音账号累计收获超8 000万粉丝关注,谷爱凌抖音平台迅速圈粉,美兰德数据显示,其抖音粉丝量已突破1 800万人.数据1 800万用科学记数法表示为( )A、 B、 C、 D、4. 如图, , FM平分 , 则( )
A、俯视图 B、主视图和俯视图 C、主视图和左视图 D、左视图和俯视图3. 2022年北京冬奥会中国队运动员微博、抖音账号累计收获超8 000万粉丝关注,谷爱凌抖音平台迅速圈粉,美兰德数据显示,其抖音粉丝量已突破1 800万人.数据1 800万用科学记数法表示为( )A、 B、 C、 D、4. 如图, , FM平分 , 则( )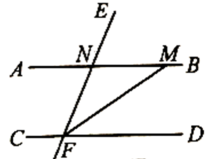 A、 B、 C、 D、5. 对称美在生活中处处可见,下列是历届冬奥会的会徽,其中既是中心对称图形又是轴对称图形的是( )A、
A、 B、 C、 D、5. 对称美在生活中处处可见,下列是历届冬奥会的会徽,其中既是中心对称图形又是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 6. 如图,在中, , 把沿直线BC向右平移6个单位长度得到 , 则四边形的面积是( )
6. 如图,在中, , 把沿直线BC向右平移6个单位长度得到 , 则四边形的面积是( ) A、40 B、56 C、60 D、647. 下列计算正确的是( )A、 B、 C、 D、8. 莱芜区某中学在预防新冠肺炎期间,要求学生每天测量体温,九(1)班一名同学记录了他一周的体温情况,并将统计结果绘制了如图所示的折线统计图.下列说法错误的是( )
A、40 B、56 C、60 D、647. 下列计算正确的是( )A、 B、 C、 D、8. 莱芜区某中学在预防新冠肺炎期间,要求学生每天测量体温,九(1)班一名同学记录了他一周的体温情况,并将统计结果绘制了如图所示的折线统计图.下列说法错误的是( ) A、这一周体温数据的众数是36.2 B、这一周体温数据的中位数是36.3 C、这一周体温数据的平均数是36.3 D、这一周体温数据的极差是0.19. 如图,中, , 利用尺规在BC,BA上分别截取BE,BD,使 . 分别以D,E为圆心、以大于的长为半径作弧,两弧在内交于点F;作射线BF交AC于点G,若 , P为AB上一动点,则GP的最小值为( )
A、这一周体温数据的众数是36.2 B、这一周体温数据的中位数是36.3 C、这一周体温数据的平均数是36.3 D、这一周体温数据的极差是0.19. 如图,中, , 利用尺规在BC,BA上分别截取BE,BD,使 . 分别以D,E为圆心、以大于的长为半径作弧,两弧在内交于点F;作射线BF交AC于点G,若 , P为AB上一动点,则GP的最小值为( )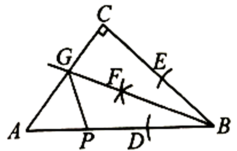 A、 B、3 C、 D、610. 反比例函数与正比例函数的图象如图所示,点 , 点与点均在反比例函数的图象上,点B在直线上,四边形是平行四边形,则B点的坐标为( )
A、 B、3 C、 D、610. 反比例函数与正比例函数的图象如图所示,点 , 点与点均在反比例函数的图象上,点B在直线上,四边形是平行四边形,则B点的坐标为( ) A、 B、 C、 D、11. 如图,在菱形ABCD中, , 对角线AC、BD相交于点O,点M在线段AC上,且 , 点P是线段BD上的一个动点,则的最小值是( )
A、 B、 C、 D、11. 如图,在菱形ABCD中, , 对角线AC、BD相交于点O,点M在线段AC上,且 , 点P是线段BD上的一个动点,则的最小值是( ) A、2 B、 C、4 D、12. 定义:平面直角坐标系中,点的横坐标x的绝对值表示为 , 纵坐标y的绝对值表示为 , 我们把点的横坐标与纵坐标的绝对值之和叫做点的折线距离,记为(其中的“+”是四则运算中的加法),若抛物线与直线只有一个交点M,已知点M在第一象限,且 , 令 , 则t的取值范围为( )A、 B、 C、 D、
A、2 B、 C、4 D、12. 定义:平面直角坐标系中,点的横坐标x的绝对值表示为 , 纵坐标y的绝对值表示为 , 我们把点的横坐标与纵坐标的绝对值之和叫做点的折线距离,记为(其中的“+”是四则运算中的加法),若抛物线与直线只有一个交点M,已知点M在第一象限,且 , 令 , 则t的取值范围为( )A、 B、 C、 D、二、填空题
-
13. 分解因式: .14. 在一个不透明布袋中装有除颜色外没有其他区别的1个红球和2个白球,搅匀后从中摸出一个球,放回搅匀,再摸出一个球,两次都摸出红球的概率是 .15. 代数式与代数式的和为1,则x= .16. 一个正多边形的每一个内角比每一个外角的3倍还大 , 则这个正多边形的边数为 .17. 如图,在扇形中,已知 , , 过的中点C作 , , 垂足分别为D、E,则图中阴影部分的面积为 .
 18. 如图,将矩形纸片ABCD折叠(AD>AB),使AB落在AD上,AE为折痕,然后将矩形纸片展开铺在一个平面上,E点不动,将BE边折起,使点B落在AE上的点G处,连接DE,若DE=EF,CE=1,则AD= .
18. 如图,将矩形纸片ABCD折叠(AD>AB),使AB落在AD上,AE为折痕,然后将矩形纸片展开铺在一个平面上,E点不动,将BE边折起,使点B落在AE上的点G处,连接DE,若DE=EF,CE=1,则AD= .
三、解答题
-
19.(1)、(2)、先化简,再求值: , 再从不等式中选择一个你喜欢的整数解代入求值.20. 为了解学生每天的睡眠情况,某初中学校从全校800名学生中随机抽取了40名学生,调查了他们平均每天的睡眠时间(单位:h),统计结果如下:
9,8,10.5,7,9,8,10,9.5,8,9,9.5,8,9.5,9,8.5,7.5,10,9.5,8,9,7,9.5,8.5,9,7,9,9,7.5,8.5,8.5,9,8,7.5,9.5,10,9.5,8.5,9,8,9.
在对这些数据整理后,绘制了如下的统计图表:
睡眠时间分布情况图

睡眠时间分组统计表
组别
睡眠时间分组
人数(频数)
1
m
2
12
3
n
4
4
请根据以上信息,解答下列问题:
(1)、m= , n= , a= , b=;(2)、抽取的这40名学生平均每天睡眠时间的中位数落在组(填组别);(3)、如果按照学校要求,学生平均每天的睡眠时间应不少于9h,请估计该校学生中睡眠时间符合要求的人数.21. 在中, , 以AC为直径的与AB相交点D、E是BC的中点. (1)、判断ED与的位置关系,并说明理由;(2)、若的半径为3, , 求的长.22. 如图,5G信号塔AB建在垂直于水平面的悬崖边B点处(点A、B、C在同一直线上).某测量员从悬崖底C点出发沿水平方向前行60米到D点,再沿斜坡DE方向前行52米到E点(点A、B、C、D、E在同一平面内),在点E处测得5G信号塔顶端A的仰角为 , 悬崖BC的高为78米,斜坡DE的坡度户 . (参考数据: . )
(1)、判断ED与的位置关系,并说明理由;(2)、若的半径为3, , 求的长.22. 如图,5G信号塔AB建在垂直于水平面的悬崖边B点处(点A、B、C在同一直线上).某测量员从悬崖底C点出发沿水平方向前行60米到D点,再沿斜坡DE方向前行52米到E点(点A、B、C、D、E在同一平面内),在点E处测得5G信号塔顶端A的仰角为 , 悬崖BC的高为78米,斜坡DE的坡度户 . (参考数据: . ) (1)、求斜坡DE的高EH的长;(2)、求信号塔AB的高度.23. 某药店购进甲、乙两种医用口罩,已知甲种口罩每袋的售价比乙种口罩多5元.小刘从该药店购买2袋甲种口罩和3袋乙种口罩共花费110元.(1)、该药店甲、乙两种口罩每袋的售价各是多少元?(2)、根据消费者需求,药店决定用不超过1900元购进甲、乙两种口罩共100袋,且甲种口罩的数量至少比乙种口罩多30袋,已知甲种口罩每袋的进价为20元,乙种口罩每袋的进价为16元.若使药店获利最大,应该购进甲、乙两种口罩各多少袋,最大获利多少元?24. 四边形ABCD和四边形AMPN有公共顶点A,连接BM和DN.
(1)、求斜坡DE的高EH的长;(2)、求信号塔AB的高度.23. 某药店购进甲、乙两种医用口罩,已知甲种口罩每袋的售价比乙种口罩多5元.小刘从该药店购买2袋甲种口罩和3袋乙种口罩共花费110元.(1)、该药店甲、乙两种口罩每袋的售价各是多少元?(2)、根据消费者需求,药店决定用不超过1900元购进甲、乙两种口罩共100袋,且甲种口罩的数量至少比乙种口罩多30袋,已知甲种口罩每袋的进价为20元,乙种口罩每袋的进价为16元.若使药店获利最大,应该购进甲、乙两种口罩各多少袋,最大获利多少元?24. 四边形ABCD和四边形AMPN有公共顶点A,连接BM和DN. (1)、如图1,若四边形ABCD和四边形AMPN都是正方形,当正方形AMPN绕点A旋转角()时,BM和DN的数量关系是 , 位置关系是;(2)、如图2,若四边形ABCD和四边形AMPN都是矩形,且 , 判断BM和DN的数量关系和位置关系,并说明理由;(3)、在(2)的条件下,若 , 矩形AMPN绕点A逆时针旋转角(),当时,求线段DN的长.25. 抛物线的顶点坐标为 , 与x轴交于点两点,与y轴交于点C,点M是抛物线上的动点.
(1)、如图1,若四边形ABCD和四边形AMPN都是正方形,当正方形AMPN绕点A旋转角()时,BM和DN的数量关系是 , 位置关系是;(2)、如图2,若四边形ABCD和四边形AMPN都是矩形,且 , 判断BM和DN的数量关系和位置关系,并说明理由;(3)、在(2)的条件下,若 , 矩形AMPN绕点A逆时针旋转角(),当时,求线段DN的长.25. 抛物线的顶点坐标为 , 与x轴交于点两点,与y轴交于点C,点M是抛物线上的动点.
 (1)、求这条抛物线的函数表达式;(2)、如图1,若点M在直线BC上方抛物线上,连接AM交BC于点E,求的最大值及此时点M的坐标;(3)、如图2,已知点 , 是否存在点M,使得?若存在,求出点M的坐标;若不存在,请说明理由.
(1)、求这条抛物线的函数表达式;(2)、如图1,若点M在直线BC上方抛物线上,连接AM交BC于点E,求的最大值及此时点M的坐标;(3)、如图2,已知点 , 是否存在点M,使得?若存在,求出点M的坐标;若不存在,请说明理由.