山东省菏泽市牡丹区2022年中考二模数学试题
试卷更新日期:2022-05-31 类型:中考模拟
一、单选题
-
1. 在实数 , -3, , 中,最小的数是( )A、 B、-3 C、 D、2. 下列图形是用数学家的名字命名的,其中既是轴对称图形又是中心对称图形的是( )A、
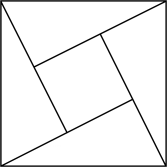 赵爽弦图
B、
赵爽弦图
B、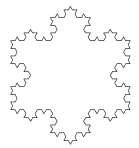 科勒曲线
C、
科勒曲线
C、 笛卡尔心形曲线
D、
笛卡尔心形曲线
D、 斐波那契螺旋曲线
3. 如图所示的是一个正方体的展开图,把展开图折叠成小正方体,和“富”字一面相对面的字是( )
斐波那契螺旋曲线
3. 如图所示的是一个正方体的展开图,把展开图折叠成小正方体,和“富”字一面相对面的字是( ) A、强 B、明 C、文 D、主4. 下列运算正确的是( )A、 B、 C、 D、5.
A、强 B、明 C、文 D、主4. 下列运算正确的是( )A、 B、 C、 D、5.如图,将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上.如果∠2=60°,那么∠1的度数为( )
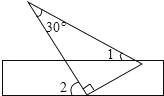 A、60° B、50° C、40° D、30°6. 如图,已知▱AOBC的顶点O(0,0),A(﹣1,2),点B在x轴正半轴上按以下步骤作图:①以点O为圆心,适当长度为半径作弧,分别交边OA,OB于点D,E;②分别以点D,E为圆心,大于 DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G,则点G的坐标为( )
A、60° B、50° C、40° D、30°6. 如图,已知▱AOBC的顶点O(0,0),A(﹣1,2),点B在x轴正半轴上按以下步骤作图:①以点O为圆心,适当长度为半径作弧,分别交边OA,OB于点D,E;②分别以点D,E为圆心,大于 DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G,则点G的坐标为( )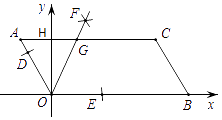 A、( ﹣1,2) B、( ,2) C、(3﹣ ,2) D、( ﹣2,2)7. 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为 ,且经过点(2,0). 下列说法:①abc<0;②-2b+c=0;③4a+2b+c<0;④若 , 是抛物线上的两点,则y1<y2;⑤ b>m(am+b) (其中m≠ ).其中说法正确的是( )
A、( ﹣1,2) B、( ,2) C、(3﹣ ,2) D、( ﹣2,2)7. 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为 ,且经过点(2,0). 下列说法:①abc<0;②-2b+c=0;③4a+2b+c<0;④若 , 是抛物线上的两点,则y1<y2;⑤ b>m(am+b) (其中m≠ ).其中说法正确的是( )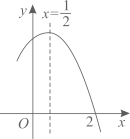 A、①②④⑤ B、①②④ C、①④⑤ D、③④⑤8. 如图,在正方形ABCD中,顶点 , , 点F是BC的中点,CD与y轴交于点E,AF与BE交于点G,将正方形ABCD绕点O顺时针旋转,每次旋转90°,则第2022次旋转结束时,点G的坐标为( )
A、①②④⑤ B、①②④ C、①④⑤ D、③④⑤8. 如图,在正方形ABCD中,顶点 , , 点F是BC的中点,CD与y轴交于点E,AF与BE交于点G,将正方形ABCD绕点O顺时针旋转,每次旋转90°,则第2022次旋转结束时,点G的坐标为( )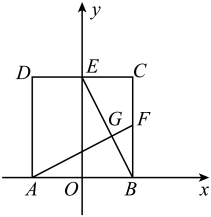 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 2021年10月16日,神舟十三号载人飞船顺利将三位宇航员送入太空,飞船平均飞行速度为每小时2844万米,用科学记数法表示2844万为 .10. 已知x=2,x+y=3,则x2y+xy2= .11. 满足不等式组的最小整数解是 .12. 对于实数a、b,定义一种新运算“ ”为: ,这里等式右边是实数运算.例如: ,则方程 的解是 .13. 如图,已知矩形ABCD与矩形EFGO是位似图形,点P是位似中心,若点B、F的坐标分别为、 , 则点P的坐标为 .
 14. 如图,点 是双曲线 在第二象限分支上的一个动点,连接 并延长交另一分支于点 ,以 为底作等腰 ,且 ,点 在第一象限,随着点 的运动点 的位置也不断变化,但点 始终在双曲线 上运动,则 的值为.
14. 如图,点 是双曲线 在第二象限分支上的一个动点,连接 并延长交另一分支于点 ,以 为底作等腰 ,且 ,点 在第一象限,随着点 的运动点 的位置也不断变化,但点 始终在双曲线 上运动,则 的值为.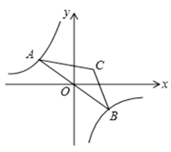
三、解答题
-
15. 计算: .16. 先化简,再求值 ,其中 满足
17. 如图,在四边形ABCD中,AD∥BC,对角线BD的垂直平分线与边AD,BC分别相交于点M,N. (1)、求证:四边形BNDM是菱形;(2)、若BD=24,MN=10,求菱形BNDM的周长.18. 某校计划购买一批篮球和足球,已知购买2个篮球和1个足球共需320元,购买3个篮球和2个足球共需540元.
(1)、求证:四边形BNDM是菱形;(2)、若BD=24,MN=10,求菱形BNDM的周长.18. 某校计划购买一批篮球和足球,已知购买2个篮球和1个足球共需320元,购买3个篮球和2个足球共需540元.
(1)、求每个篮球和每个足球的售价;(2)、如果学校计划购买这两种球共50个,总费用不超过5500元,那么最多可购买多少个足球?
19. 为了丰富学生社会实践活动,学校组织学生到红色文化基地和人工智能科技馆参观学习.如图,学校在点处,位于学校的东北方向,位于学校南偏东方向,在的南偏西方向的处.求学校和红色文化基地之间的距离. 20. 如图,在平面直角坐标系 中,一次函数 的图象经过点 ,与反比例函数 的图象交于 .
20. 如图,在平面直角坐标系 中,一次函数 的图象经过点 ,与反比例函数 的图象交于 .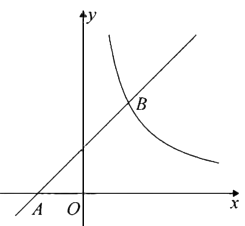 (1)、求一次函数和反比例函数的表达式;(2)、设 是直线 上一点,过 作 轴,交反比例函数 的图象于点 ,若 为顶点的四边形为平行四边形,求点 的坐标.
(1)、求一次函数和反比例函数的表达式;(2)、设 是直线 上一点,过 作 轴,交反比例函数 的图象于点 ,若 为顶点的四边形为平行四边形,求点 的坐标.
21. 为了庆祝建党100周年,歌颂党的光辉历史,育星中学举行了“童心向党·青春追梦”主题朗诵比赛.比赛结束后对参赛学生的成绩进行了统计,绘制出如下的统计图①和②.请根据相关信息解答下列问题: (1)、图①中m的值为 , 这组比赛成绩数据的平均数是 , 众数是 , 中位数是;(2)、学校决定从获得10分的1名男生和2名女生中任选两名学生参加区级比赛,请用列表法或画树状图法求选中一名男生一名女生的概率.22. 如图,AB是的直径,点C为上一点,PC切于点C,交PC的延长线于点E,AE交于点D,PC与AB的延长线相交于点P,连结AC、BC.
(1)、图①中m的值为 , 这组比赛成绩数据的平均数是 , 众数是 , 中位数是;(2)、学校决定从获得10分的1名男生和2名女生中任选两名学生参加区级比赛,请用列表法或画树状图法求选中一名男生一名女生的概率.22. 如图,AB是的直径,点C为上一点,PC切于点C,交PC的延长线于点E,AE交于点D,PC与AB的延长线相交于点P,连结AC、BC.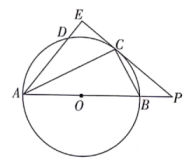 (1)、求证:AC平分;(2)、若 , , 求AB的长.23.
(1)、求证:AC平分;(2)、若 , , 求AB的长.23.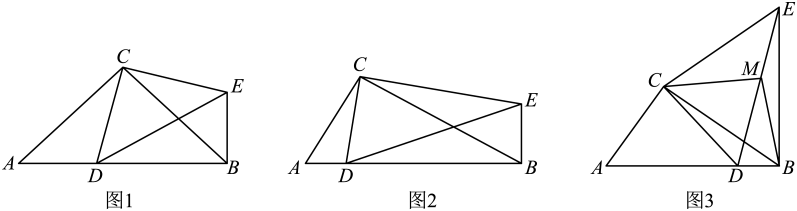 (1)、问题发现
(1)、问题发现如图1,在Rt△ABC和Rt△CDE中, , , 点D是线段AB上一动点,连接BE.填空:
①的值为;
②的度数为 .
(2)、类比探究如图2,在Rt△ABC和Rt△CDE中, , , 点D是线段AB上一动点,连接BE.请判断的值及的度数,并说明理由;
(3)、拓展延伸如图3,在(2)的条件下,取线段DE的中点M,连接BM、CM,若 , 则当△CBM是直角三角形时,求线段BE的长.
24. 如图,开口向上的抛物线与x轴交于A( , 0)、B( , 0)两点,与y轴交于点C,且AC⊥BC,其中 , 是方程x2+3x﹣4=0的两个根. (1)、求点C的坐标,并求出抛物线的表达式;(2)、垂直于线段BC的直线l交x轴于点D,交线段BC于点E,连接CD,求△CDE的面积的最大值及此时点D的坐标;(3)、在(2)的结论下,抛物线的对称轴上是否存在点P,使得△PDE是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
(1)、求点C的坐标,并求出抛物线的表达式;(2)、垂直于线段BC的直线l交x轴于点D,交线段BC于点E,连接CD,求△CDE的面积的最大值及此时点D的坐标;(3)、在(2)的结论下,抛物线的对称轴上是否存在点P,使得△PDE是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.