山东省荷泽市东明县2022年九年级中考三模数学试题
试卷更新日期:2022-05-31 类型:中考模拟
一、单选题
-
1. 2022的相反数是( )A、 B、 C、2022 D、-20222. 下列图案中,是轴对称图形但不是中心对称图形的是( )A、
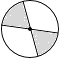 B、
B、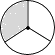 C、
C、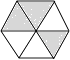 D、
D、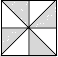 3. 生物学家发现新型冠状病毒的直径约为0.00012mm,数据0.00012用科学记数法表示正确的是( )A、 B、 C、 D、4. 如图是一个几何体的三视图(图中尺寸单位: ),根据图中所示数据求得这个几何体的侧面积是( )
3. 生物学家发现新型冠状病毒的直径约为0.00012mm,数据0.00012用科学记数法表示正确的是( )A、 B、 C、 D、4. 如图是一个几何体的三视图(图中尺寸单位: ),根据图中所示数据求得这个几何体的侧面积是( )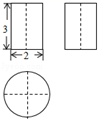 A、 B、 C、 D、5. 当 时,关于 的一元二次方程 的根的情况为( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定6. 如图,AB是⊙O的直径,点C,D,E在⊙O上,若∠AED=20°,则∠BCD的度数为( )
A、 B、 C、 D、5. 当 时,关于 的一元二次方程 的根的情况为( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定6. 如图,AB是⊙O的直径,点C,D,E在⊙O上,若∠AED=20°,则∠BCD的度数为( ) A、100° B、110° C、115° D、120°7. 如图,点P是▱ABCD边上一动点,沿A→D→C→B的路径移动,设P点经过的路径长为x,△BAP的面积是y,则下列能大致反映y与x的函数关系的图象是( )
A、100° B、110° C、115° D、120°7. 如图,点P是▱ABCD边上一动点,沿A→D→C→B的路径移动,设P点经过的路径长为x,△BAP的面积是y,则下列能大致反映y与x的函数关系的图象是( )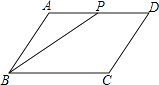 A、
A、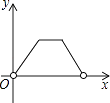 B、
B、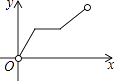 C、
C、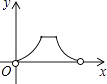 D、
D、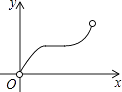 8. 一次函数y=ax+b(a≠0)与二次函数y=ax2+bx+c(a≠0)在同一平面直角坐标系中的图象可能是( )
8. 一次函数y=ax+b(a≠0)与二次函数y=ax2+bx+c(a≠0)在同一平面直角坐标系中的图象可能是( )
A、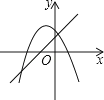 B、
B、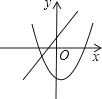 C、
C、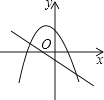 D、
D、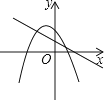
二、填空题
-
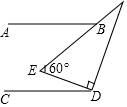
9. 把多项式分解因式的结果是 .10. 一组2,2x,y,12中,唯一的众数是12,平均数是10,这数据的中位数是 .11. 不等式组的解集为.12. 如图所示,直角三角板的60°角压在一组平行线上, , , 则度.
 13. 如图,矩形中,点G,E分别在边上,连接 , 将和分别沿折叠,使点B,C恰好落在上的同一点,记为点F.若 , 则 .
13. 如图,矩形中,点G,E分别在边上,连接 , 将和分别沿折叠,使点B,C恰好落在上的同一点,记为点F.若 , 则 .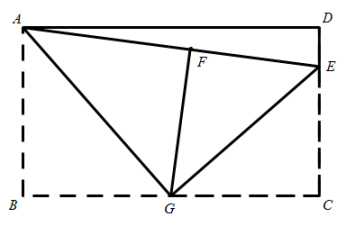 14. 有一个数值转换器,原理如下图所示,当输入x的值为16时,输出y的值是 .
14. 有一个数值转换器,原理如下图所示,当输入x的值为16时,输出y的值是 .
三、解答题
-
15. 计算: .16. 先化简,再求值: , 其中 .17. 在如图菱形 中,点 是 边上一点,连接 ,点 是 上的两点,连接 , ,使得 , .
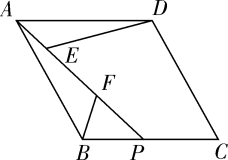 (1)、求证: ;(2)、求证: .18. 现有两块面积相同的小麦试验田,第一块种植原品种,第二块种植新品种,结果分别收获小麦12000kg和14000kg.已知第一块试验田每公顷的产量比第二块少1500kg,求第一块试验田每公顷的产量.19. 2022年冬季奥运会在北京举行,激起了人们对冰雪运动的极大热情.如图是某滑雪场高级雪道缆车线路示意图,滑雪者从点出发,途经点后到达终点 , 其中 , , 且段的运行路线与水平面的夹角为30°,段的运行路线与水平面的夹角为37°,求从点运行到点垂直上升的高度.(结果保留整数;参考数据: , , )
(1)、求证: ;(2)、求证: .18. 现有两块面积相同的小麦试验田,第一块种植原品种,第二块种植新品种,结果分别收获小麦12000kg和14000kg.已知第一块试验田每公顷的产量比第二块少1500kg,求第一块试验田每公顷的产量.19. 2022年冬季奥运会在北京举行,激起了人们对冰雪运动的极大热情.如图是某滑雪场高级雪道缆车线路示意图,滑雪者从点出发,途经点后到达终点 , 其中 , , 且段的运行路线与水平面的夹角为30°,段的运行路线与水平面的夹角为37°,求从点运行到点垂直上升的高度.(结果保留整数;参考数据: , , )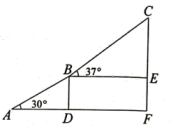 20. 如图,正比例函数y=2x的图象与反比例函数y= 的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.
20. 如图,正比例函数y=2x的图象与反比例函数y= 的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2. (1)、求k的值;(2)、x轴上是否存在一点D , 使△ABD为直角三角形?若存在,求出点D的坐标;若不存在,请说明理由.21. 某学校利用“世界献血日”开展自愿义务献血活动,经过检测,献血者血型有“A,B,AB,O”四种类型,随机抽取部分献血结果进行统计,根据结果制作了如图两幅不完整统计图表:
(1)、求k的值;(2)、x轴上是否存在一点D , 使△ABD为直角三角形?若存在,求出点D的坐标;若不存在,请说明理由.21. 某学校利用“世界献血日”开展自愿义务献血活动,经过检测,献血者血型有“A,B,AB,O”四种类型,随机抽取部分献血结果进行统计,根据结果制作了如图两幅不完整统计图表:血型统计表
血型
A
B
AB
O
人数
10
5
 (1)、本次随机抽取献血者人数为人,图中m=;(2)、补全表中的数据;(3)、现有4个自愿献血者,2人为O型,1人为A型,1人为B型,若在4人中随机挑选2人,利用树状图或列表法求两人血型均为O型的概率.22. 如图, 为 上一点,点 在直径 的延长线上,且 .
(1)、本次随机抽取献血者人数为人,图中m=;(2)、补全表中的数据;(3)、现有4个自愿献血者,2人为O型,1人为A型,1人为B型,若在4人中随机挑选2人,利用树状图或列表法求两人血型均为O型的概率.22. 如图, 为 上一点,点 在直径 的延长线上,且 .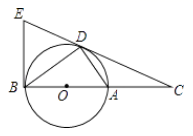 (1)、求证: ;(2)、求证: 是 的切线;(3)、过点 作 的切线 交 的延长线于点 ,若 , ,求 的长.23. 阅读材料,回答问题:
(1)、求证: ;(2)、求证: 是 的切线;(3)、过点 作 的切线 交 的延长线于点 ,若 , ,求 的长.23. 阅读材料,回答问题:小聪学完了“锐角三角函数”的相关知识后,通过研究发现:如图1,在Rt△ABC中,如果∠C=90°,∠=30°,BC═a=1,AC=b= , AB=c=2,那么==2.通过上网查阅资料,他又知“sin90°=1”,因此他得到“在含30°角的直角三角形中,存在着==的关系.
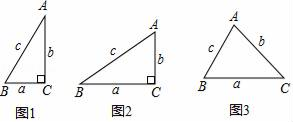
这个关系对于一般三角形还适用吗?为此他做了如下的探究:
(1)、如图2,在R△ABC中,∠C=90°,BC=a,AC=b,AB=C,请判断此时“==”的关系是否成立?答:(2)、完成上述探究后,他又想“对于任意的锐角△ABC,上述关系还成立吗?”因此他又继续进行了如下的探究:如图3,在锐角△ABC中,BC=a,AC=b,AB=c,请判断此时“ ==”的关系是否成立?并证明你的判断.(提示:过点C作CD⊥AB于D,过点A作AH⊥BC,再结合定义或其它方法证明).
24. 在平面直角坐标系中,二次函数的图象与x轴的交点为 , 两点,与y轴交于点 , 顶点为D,其对称轴与x轴交于点E.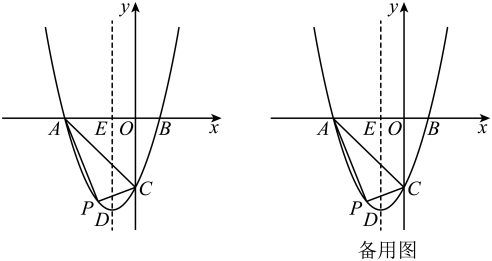 (1)、求二次函数的解析式;(2)、点P为第三象限内抛物线上一点,的面积记为S,求S的最大值及此时点P的坐标.
(1)、求二次函数的解析式;(2)、点P为第三象限内抛物线上一点,的面积记为S,求S的最大值及此时点P的坐标.