山东省东营市垦利区2022年中考二模数学试题

试卷更新日期：2022-05-31 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列各数中，比－2小的数是（）．

A、－3 B、－1 C、0 D、1

查看试题解析
2. 下列运算中，正确的是（　　）

A、2a²﹣a²＝2 B、a²·a⁴＝a⁶ C、（a²）³＝a⁵ D、a⁶÷a²＝a³

查看试题解析
3. 如图所示的几何体是由5个相同的小正方体组成，其主视图为（）

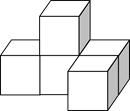A、 B、 C、 D、

查看试题解析
4. 某班级开展“好书伴成长”读书活动，统计了1至7月份该班同学每月阅读课外书的数量，绘制了折线统计图，下列说法正确的是（）

A、每月阅读课外书本数的众数是45 B、每月阅读课外书本数的中位数是58 C、从2到6月份阅读课外书的本数逐月下降 D、从1到7月份每月阅读课外书本数的最大值比最小值多45

查看试题解析
5. 从下列4个函数①y＝3x﹣2；②y＝－ $\frac{7}{x}$ （x＞0）；③y＝ $\frac{5}{x}$ ；④y＝﹣x²（x＜0）中任取一个，函数值y随自变量x的增大而增大的概率是（　　）

A、 $\frac{1}{4}$ B、 $\frac{1}{2}$ C、 $\frac{3}{4}$ D、1

查看试题解析
6. 《九章算术》是中国古代数学著作之一，书中有这样一个问题：五只雀、六只燕共重一斤，雀重燕轻，互换其中一只，恰好一样重.问：每只雀、燕的重量各为多少?设一只雀的重量为x斤，一只燕的重量为y斤，则可列方程组为（）

A、 ${\begin{cases} 5 x + 6 y = 1 \\ 5 x - y = 6 y - x \end{cases}$ B、 ${\begin{cases} 6 x + 5 y = 1 \\ 5 x + y = 6 y + x \end{cases}$ C、 ${\begin{cases} 5 x + 6 y = 1 \\ 4 x + y = 5 y + x \end{cases}$ D、 ${\begin{cases} 6 x + 5 y = 1 \\ 4 x - y = 5 y - x \end{cases}$

查看试题解析
7. 若将函数y＝2x²的图象向右平行移动1个单位，再向上平移3个单位，得到的抛物线是（）

A、y＝2（x+5）²﹣1 B、y＝2（x+5）²+1 C、y＝2（x﹣1）²+3 D、y＝2（x+1）²﹣3

查看试题解析
8. 如图，在 $⊙ O$ 中，点 $A 、 B 、 C$ 在圆上， $∠ A C B = 45^{°} ， A B = 2 \sqrt{2}$ ，则 $⊙ O$ 的半径 $O A$ 的长是（）

A、 $\sqrt{2}$ B、2 C、 $2 \sqrt{2}$ D、3

查看试题解析
9.
如图，在△ABC中，AB＞AC，点D、E分别是边AB、AC的中点，点F在BC边上，连接DE、DF、EF，则添加下列哪一个条件后，仍无法判断△FCE与△EDF全等（　　）

A、∠A=∠DFE B、BF=CF C、DF∥AC D、∠C=∠EDF

查看试题解析
10. 如图，正方形ABCD中，点F是BC边上一点，连接AF，以AF为对角线作正方形AEFG，边FG与正方形ABCD的对角线AC相交于点H，连接DG．以下四个结论：① $∠ E A B = ∠ G A D$ ；②△AFC∽△AGD；③2AE²＝AH•AC；④DG⊥AC．其中正确的个数为（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 据中国电影数据信息网消息，截止到 $2021$ 年 $12$ 月 $7$ 日，诠释伟大抗美援朝精神的电影 $《$ 长津湖 $》$ 累计票房已达 $57.43$ 亿元.将 $57.43$ 亿元用科学记数法表示元.

查看试题解析
12. 分解因式：mn²-2mn+m=

查看试题解析
13. 已知一次函数y=kx+b的图象经过A（1，﹣1），B（﹣1，3）两点，则k0（填“＞”或“＜”）

查看试题解析
14. 已知圆锥的母线与高的夹角为30°，母线长为6，则这个圆锥的侧面积为．

查看试题解析
15. 如图，在等腰 $Rt △ A B C$ 中， $∠ B A C = 90 °$ ， $B C = 4 \sqrt{2}$ .分别以点 $A$ ， $B$ ， $C$ 为圆心，以 $\frac{1}{2} A B$ 的长为半径画弧分别与 $△ A B C$ 的边相交，则图中阴影部分的面积为.（结果保留 $π$ ）

查看试题解析
16. 如图，A，B两点分别在x轴正半轴，y轴正半轴上且 $∠ B A O = 30 °$ ， $A B = 4 \sqrt{3}$ ，将△AOB沿AB翻折得 $△$ ADB，反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图像恰好经过D点，则k的值是．

查看试题解析
17. 如图，在菱形 $A B C D$ 中， $A C = 6 \sqrt{3}$ ， $B D = 6$ ， E是 $B C$ 边的中点，P，M分别是 $A C$ ， $A B$ 上的动点，连接 $P E$ ， $P M$ ，则 $P E + P M$ 的最小值是．

查看试题解析
18. 如图，一次函数y=x与反比例函数 $y = \frac{1}{x}$ （x＞0）的图象交于点A，过点A作AB⊥OA，交x轴于点B；作 $B A_{1} ∥ O A$ ，交反比例函数图象于点A₁；过点A₁作A₁ B₁⊥A₁B交x轴于点B₁；再作 $B_{1} A_{2} ∥ B A_{1}$ ，交反比例函数图象于点A₂ ，依次进行下去······则点A₂₀₂₂的横坐标为.

查看试题解析

三、解答题

19.

(1)、计算： $| 1 - \sqrt{3} | + \sqrt[3]{27} - 2 c o s 30 ° + {(- \frac{1}{3})}^{- 1} - {(2020 - π)}^{0}$ ．

(2)、先化简： $(\frac{x^{2} - 2 x}{x^{2} - 4 x + 4} - \frac{1}{x - 2}) \div \frac{x^{2} - x}{x^{2} - 4}$ ，再从不等式﹣2≤x＜3中选取一个合适的整数，代入求值．

查看试题解析
20. 目前中学生带手机进校园现象越来越受到社会关注，针对这种现象，某校数学兴趣小组的同学随机调查了学校若干名家长对“中学生带手机”现象的态度（态度分为：A．无所谓；B．基本赞成；C．赞成；D．反对），并将调查结果绘制成频数折线统计图1和扇形统计图2（不完整）．请根据图中提供的信息，解答下列问题：

(1)、此次抽样调查中，共调查了多少名中学生家长；

(2)、求出图2中扇形C所对的圆心角的度数，并将图1补充完整；

(3)、在此次调查活动中，初三（1）班和初三（2）班各有2位家长对中学生带手机持反对态度，现从这4位家长中选2位家长参加学校组织的家校活动，用列表法或画树状图的方法求选出的2人来自不同班级的概率．

查看试题解析
21. 如图，AB为⊙O的直径，C、D为⊙O上的两点，且AC平分∠BAD，过点C作直线EF⊥AD，交AD的延长线于点E．

(1)、证明：EF是⊙O的切线；

(2)、若AE= $\frac{16}{5}$ ，圆O的半径是 $\frac{5}{2}$ ，求AC的长．

查看试题解析
22. 如图，某旅游景区为方便游客，修建了一条东西走向的栈道AB，栈道AB与景区道路CD平行．在C处测得栈道一端A位于北偏西45°方向，在D处测得栈道另一端B位于北偏东32°方向．已知AC＝60 m ，CD＝46 m，求栈道AB的长（结果保留整数）．参考数据：sin32° ≈ 0.53，cos32° ≈ 0.85，tan32° ≈ 0.62， $\sqrt{2}$ ≈ 1.414.

查看试题解析
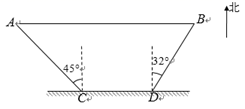23. 就目前情况，新冠肺炎疫情防控一点也不能放松，“戴口罩､勤洗手､少聚会”仍是疫情防控的有效措施．为保证防疫口罩供应，某医药公司保持每月生产甲､乙两种型号的防疫口罩共20万只，且所有口罩当月全部售出，其中成本､售价如下表：

口罩型号

甲

乙

成本（元/只）

1

3

售价（元/只）

1.5

6

(1)、该公司去年十二月份的口罩销售总收入为39万元，求该月公司生产甲､乙两种型号的口罩分别是多少万只?

(2)、设该公司每个月生产甲种型号口罩a万只，月利润为w万元，求w与a的函数关系式（不要求写自变量的取值范围）；

(3)、如果公司在今年一月份投入口罩生产的总成本不超过28万元，应怎样安排甲､乙两种型号防疫口罩的产量，可使本月公司所获利润最大?并求出最大利润．

查看试题解析
24. △ABC中，AB＝AC，∠BAC＝90°，点D，E分别是AC，BC的中点，点P是直线DE上一点，连接AP，将线段PA绕点P顺时针旋转90°得到线段PM，连接AM，CM．

(1)、问题发现：如图（1），当点P与点D重合时，线段CM与PE的数量关系是， ∠ACM＝．

(2)、探究证明：当点P在射线ED上运动时（不与点E重合），（1）中结论是否一定成立？请仅就图（2）中的情形给出证明．

查看试题解析
25. 已知抛物线 $y = a x^{2} + b x + 3$ 的图象与x轴相交于点A和点 $B (1 ， 0)$ ，与y轴交于点C，连接AC，有一动点D在线段AC上运动，过点D作x轴的垂线，交抛物线于点E，交x轴于点F，AB＝4，设点D的横坐标为m．

(1)、求抛物线的解析式；

(2)、连接AE、CE，当 $△ A C E$ 的面积最大时，点D的坐标是；

(3)、当 $m = - 2$ 时，在平面内是否存在点Q，使以B，C，E，Q为顶点的四边形为平行四边形？若存在，请求出点Q的坐标；若不存在，请说明理由．

查看试题解析

口罩型号	甲	乙
成本（元/只）	1	3
售价（元/只）	1.5	6