山东省德州市庆云县2022年九年级下学期第二次练兵考试数学试题

试卷更新日期：2022-05-31 类型：中考模拟

进入出卷网下载

一、单选题

1. －2的绝对值是（）

A、2 B、－2 C、 $2^{- 1}$ D、 $- \frac{1}{2}$

查看试题解析
2. 下列计算正确的是（）

A、 $2 a + 3 a = 6 a$ B、 $(- 2 a)^{2} = 4 a^{2}$ C、 $- 2 (3 a + 1) = - 6 a - 1$ D、 $(a + 2) (a - 2) = a^{2} - 2$

查看试题解析
3. 如图是一个小正方体的展开图，把展开图折叠成小正方体后，与“数”这个汉字相对的面上的汉字是（）

A、我 B、很 C、喜 D、欢

查看试题解析
4. 一副三角板按如图所示的位置摆放，若BC∥DE，则∠1的度数是（）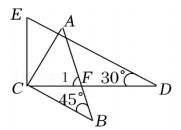

A、65° B、70° C、75° D、80°

查看试题解析
5. 下列关于反比例函数 $y = \frac{5}{x}$ 的描述中，正确的是（）

A、图象在二、四象限 B、当 $x < 0$ 时，y随x的增大而减小 C、点（ $(- 1 ， 5)$ 在反比例函数图象上 D、当 $x < 1$ 时， $y > 5$

查看试题解析
6. 如图，PA、PB是⊙O切线，A、B为切点，点C在⊙O上，且∠ACB＝55°，则∠APB等于（）

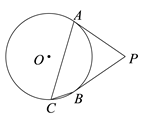A、55° B、70° C、110° D、125°

查看试题解析
7. 已知一元二次方程x²﹣10x＋24＝0的两个根是菱形的两条对角线长，则这个菱形的面积为（）

A、6 B、10 C、12 D、24

查看试题解析
8. 如图，在纸上剪下一个圆形和一个扇形的纸片，使之恰好能围成一个圆锥模型.若圆的半径为r，扇形的半径为R，扇形的圆心角等于90°，则r与R之间的关系是（）

A、R＝2r； B、 $R = \sqrt{3} r$ ； C、R＝3r； D、R＝4r.

查看试题解析
9. 下列命题中，假命题的是（）

A、顺次连接对角线垂直的四边形的四边中点所成的图形是矩形 B、各边对应成比例的两个多边形相似 C、反比例函数的图象既是轴对称图形，也是中心对称图形 D、已知二次函数 $y = x^{2} - 1$ ，当 $x < 0$ 时，y随x的增大而减小

查看试题解析
10. 如图，在 $△ A B C$ 中， $A B = 4$ ， $A C = 3$ ， $B C = 5$ ，将 $△ A B C$ 沿着点A到点C的方向平移到 $△ D E F$ 的位置，图中阴影部分面积为4，则平移的距离为（）

A、 $3 - \sqrt{6}$ B、 $\sqrt{6}$ C、 $3 + \sqrt{6}$ D、 $2 \sqrt{6}$

查看试题解析
11. 如图，在边长为3的菱形ABCD中，点P从A点出发，沿A→B→C→D运动，速度为每秒3个单位；点Q同时从A点出发，沿A→D运动，速度为每秒1个单位，则 $Δ A P Q$ 的面积S关于时间 $t$ 的函数图象大致为（）

A、 B、 C、 D、

查看试题解析
12. 如图，方格纸中小正方形的边长为1， $△ A B C$ 的三个顶点都在小正方形的格点上，下列结论：① $△ A B C$ 的形状是等腰三角形；② $△ A B C$ 的周长是 $2 \sqrt{10} + \sqrt{2}$ ；③点C到 $A B$ 边的距离是 $\frac{3}{8} \sqrt{10}$ ；④ $t a n ∠ A C B$ 的值为2，正确的个数为（）

A、0个 B、1个 C、2个 D、3个

查看试题解析

二、填空题

13. 代数式 $\frac{1}{x - 3}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
14. 已知 $y = a x^{2} + b x + c (a \neq 0)$ ， y与x的部分对此值如下表：
x
……
－2
－1
0
2
……
y
……
－3
－4
－3
5
……
则一元二次方程 $a x^{2} + b x + c + 3 = 0$ 的解为．

查看试题解析
15. 在 $△ A B C$ 中， $A B = B C = 5$ ， $t a n ∠ A B C = \frac{4}{3}$ ，设 $B C$ 的垂直平分线与 $A B$ 的交点为D， $\frac{A D}{A B}$ 的值为．

查看试题解析
16. 已知a，b，c分别是 $R t △ A B C$ 的三条边长，c为斜边长， $∠ C = 90 °$ ，我们把关于x的形如 $y = \frac{a}{c} x + \frac{b}{c}$ 的一次函数称为“勾股一次函数”．若点 $P (- 1 ， \frac{\sqrt{3}}{3})$ 在“勾股一次函数”的图象上，且 $R t △ A B C$ 的面积是4，则c的值是．

查看试题解析
17. 某游乐园的摩天轮(如图1)有均匀分布在圆形转轮边缘的若干个座舱，人们坐在座舱中可以俯瞰美景，图2是摩天轮的示意图．摩天轮以固定的速度绕中心O顺时针方向转动，转一圈为18分钟．从小刚由登舱点P进入摩天轮开始计时，到第12分钟时，他乘坐的座舱到达图2中的点处(填A，B，C或D)，此点距地面的高度为m．

查看试题解析
18. 德国数学家莱布尼发现了如图所示的单位分数三角形（单位分数是分子为1，分母为正整效的分数），又称为莱和尼茨三角形，根据前5行的摆律，写出第6行的第三个数：．

查看试题解析

三、解答题

19. 先化简，再求值： $(x - 1) \div (x - \frac{2 x - 1}{x})$ ，其中 $x = - \sqrt{2} + 1$ ．

查看试题解析
20. 某校举行“母亲节暖心特别行动”、从全校随机调查了部分同学的爱心行动，并将其分为A，B，C，D四种类型，分别对应普通服务、送鲜花、送红包、送祝愿，现根据调查的数据绘制成如下的条形统计计图和扇形统计图．请根据两幅不完整的统计图提供的信息，解答下列问题：

(1)、该校共抽查了多少名同学的暖心行动？

(2)、求出扇形统计图中扇形B的圆心角度数？

(3)、若该校共有2400名同学，请估计该校进行送鲜花行动的同学的有多少名？

(4)、为增强学生环保意识，学校举办了环保知识竞赛、其中5名学生（3名男生，2名女生）获奖，老师若从获奖的5名学生中任选两名作为班级的“环保小卫士”，请用画树状图法或列表法，求出恰好是一名男生、一名女生的概率．

查看试题解析
21. 已知△ABC中，BC边的长为x，BC边上的高为y，△ABC的面积为3．

(1)、写出y关于x的函数关系式　　；x的取值范围是　　．

(2)、列表，得
x
…
1
2
3
4
…
y
…
　
　
　
　
…
在给出的坐标系中描点并连线；

(3)、如果A（x₁ ， y₁），B（x₂ ， y₂）是图象上的两个点，且x₁＞x₂＞0，试判断y₁ ， y₂的大小．

查看试题解析
22. 如图， $A B$ 是 $⊙ O$ 的直径，点C在 $A B$ 的延长线上， $∠ B D C = ∠ A$ ， $C E ⊥ A D$ ，交 $A D$ 的延长线于点E．

(1)、求证： $C D$ 与 $⊙ O$ 相切：

(2)、若 $C E = 4$ ， $D E = 2$ ，求 $A D$ 的长，

查看试题解析
23. 工厂生产某种消毒液，需要甲、乙两种原料，其中甲原料的单价比乙原料的单价高0.1万元，若已知用5万元购买甲种原料与用4.5万元购买乙种原料的数量相同，请同学们回到下面的问题：

(1)、甲、乙两种原料的单价各是多少？

(2)、按照生产计划需要购进甲、乙两种原料共55件，总费用不少于50万元，但不超过50.5万元，请求出有几种选购方案？

(3)、工厂每生产一吨消毒液成本为1万元，当销售价为1.4万元时，工厂日销售为1吨，经过一段时间的销售发现，价格每降低0.1万元．产品日销售增加0.4吨．定价在什么范围内，能使工厂利润不低于0.42万元？

查看试题解析
24. 折纸是同学们喜欢的手工活动之一，通过折纸我们既可以得到许多美丽的图形．同时纸的过程还蕴含着丰富的数学知识．

(1)、折纸1：如图，将正方形 $A B C D$ 沿 $B E$ 对折，使点A落在点 $A^{'}$ ，连接 $A^{'} C$ ，若 $∠ D E A^{'} = 50 °$ ，则 $∠ B A^{'} C =$ ．

(2)、折纸2：请用一个正方形纸片折出一个30°的角（不借助任何工具），在给出的正方形图形中画出你的折叠方法，并说明理由．

(3)、折纸3：如图，操作一；将边长为4的正方形片 $A B C D$ 对折，使点B、C分别与点A，D重合，再展开得到折痕 $E F$ ；操作：将正方形 $A B C D$ 沿着 $A F$ 折叠，使得点D落在点 $D^{'}$ 处；操作三：正方形纸片沿着 $F D^{'}$ 折叠再展开，折痕 $F D^{'}$ 与边 $B C$ 于点P，求线段 $B P$ 的长度．

(4)、综合应用：如图，在矩形 $A B C D$ 中， $A B = 6$ ， $B C = 8$ ，点P为 $B C$ 上的一点（不与B点重合，可以与C点重合），将 $△ A B P$ 沿着 $A P$ 折叠，点B的对应点为 $B^{'}$ ， $B^{'}$ 落在矩形的内部，连结 $B^{'} A$ ， $B^{'} D$ ，当 $△ B^{'} A D$ 为等腰三角形时，求 $△ B^{'} A D$ 的面积．

查看试题解析
25. 在平面直角坐标系 $x o y$ 中，抛物线 $y = x^{2} + 2 m x - m^{2} + 1$ ．

(1)、若点 $(2 ， - 1)$ 在抛物线上，求此时m的值以及顶点坐标；

(2)、不论m取何值时，抛物线的顶点始终在一条直线上，求该直线的解析式；

(3)、求抛物线的顶点M与原点O的距离的最小值；

(4)、若有两点 $A (- 1 ， 0)$ ， $B (1 ， 0)$ ，且该抛物线与线段 $A B$ 始终有交点，求m的取值范围．

查看试题解析

x	……	－2	－1	0	2	……
y	……	－3	－4	－3	5	……

x	…	1	2	3	4	…
y	…					…