山东省德州市陵城区2022年中考一模数学试题

试卷更新日期：2022-05-31 类型：中考模拟

进入出卷网下载

一、单选题

1. $- \frac{1}{2022}$ 相反数的是（）

A、2022 B、 $\frac{1}{2022}$ C、 $\pm \frac{1}{2022}$ D、 $- 2022$

查看试题解析
2. 为落实“双减”政策，鼓楼区教师发展中心开设“鼓老师讲作业”线上直播课.开播首月该栏目在线点击次数已达66799次，用四舍五入法将66799精确到千位所得到的近似数是（）

A、 $6.7 \times 1 0^{3}$ B、 $6.7 \times 1 0^{4}$ C、 $6.70 \times 1 0^{3}$ D、 $6.70 \times 1 0^{4}$

查看试题解析
3. 下面运算中正确的是（）

A、 $m^{2} \cdot m^{3} = m^{6}$ B、 $m^{2} + m^{2} = 2 m^{4}$ C、 $(- 3 a^{2} b)^{2} = 6 a^{4} b^{2}$ D、 $(- 2 x^{2}) \cdot (- 5 x^{4}) = 10 x^{6}$

查看试题解析
4. 某正方体的每个面上都有一个汉字，如图是它的一种展开图，那么在原正方体中，与“祝”字所在面相对的面上的汉字是（）

A、考 B、试 C、顺 D、利

查看试题解析
5. 在某校九年级模拟考试中，1班的六名学生的数学成绩如下：104，116，110，118，116，90．下列关于这组数据的描述错误的是（）

A、众数是116 B、中位数是113 C、平均数是109 D、方差是86

查看试题解析
6. 如图所示，数轴上A，B两点表示的数分别是﹣2和 $\sqrt{5}$ ，点B关于点A的对称点为C，则点C所表示的实数为（）

A、﹣4－ $\sqrt{5}$ B、2－ $\sqrt{5}$ C、﹣4＋ $\sqrt{5}$ D、4＋ $\sqrt{5}$

查看试题解析
7. 如图，以正方形ABCD的边AD为直径作一个半圆，点M是半圆上一个动点，分别以线段AM、DM为边各自向外作一个正方形，其面积分别为S₁和S₂ ，若正方形的面积为10，随点M的运动S₁＋S₂的值（）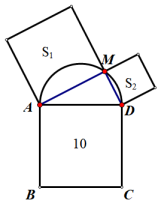

A、大于10 B、小于10 C、等于10 D、不确定

查看试题解析
8. 把一个球放在长方体收纳箱中，截面如图所示，若箱子高16cm，AB长16cm，则球的半径为（）

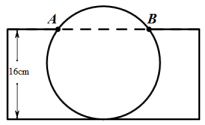A、9 B、10 C、11 D、12

查看试题解析
9. 函数y＝mx²+（m+2）x+ $\frac{1}{2}$ m+1的图象与x轴只有一个交点，则m的值为（）

A、0 B、0或2 C、0或2或﹣2 D、2或﹣2

查看试题解析
10. Rt△ABC中，∠C＝90°，∠B＝30°，点D为AB的中点，点E在边BC（包括点B、C）上，将△BDE沿着直线DE翻折得到△B′DE，设∠BDE为α，当α为（）度时，以点A、C、B′、D为顶点的四边形为菱形．

A、60° B、30° C、30°或120° D、45°或60°

查看试题解析
11. $y = {\begin{array}{l} 3 | x | (| x | \leq 1) \\ \frac{3}{| x |} (| x | > 1) \end{array}$ 的图象有如下性质：（1）函数有最大值和最小值；（2）当 $x_{1} + x_{2} = 0$ 时， $y_{1} = y_{2}$ ；（3）直线 $y = m$ 与图象的交点个数可能是0、1、2、3或4个；（4）点A是图象上的任意一点，A关于y轴的对称点为 $A^{'}$ ，则 $△ A O A^{'}$ 的面积最大值3，说法正确的有（）个

A、1 B、2 C、3 D、4

查看试题解析
12. 如图，木工师傅在板材边角处作直角时，往往使用“三弧法”，其作法是：
⑴作线段AB，分别以A，B为圆心，以AB长为半径作弧，两弧的交点为C；
⑵以C为圆心，仍以AB长为半径作弧交AC的延长线于点D；
⑶连接BD，BC．
下列说法：① $△ A C B$ 为等边三角形；② $A B^{2} + B D^{2} = A D^{2}$ ；③ $S_{Δ A B C} = \frac{1}{3} S_{Δ A B D}$ ；④ $s i n^{2} ∠ A B C + s i n^{2} ∠ D B C = 1$ ，正确的个数有（）个

A、4 B、3 C、2 D、1

查看试题解析

二、解答题

13. 先化简再求值： $(\frac{2}{a + 1} + \frac{a + 2}{a^{2} - 1}) \div \frac{a}{a + 1}$ ，其中 $a = \sqrt{5} - 1$

查看试题解析
14. 山东省教育厅副厅长孙晓筠在青少年体育工作会议上指出：“自2022年起将逐步提高中考体育科目考试分值占比”，王老师为调动学生参加体育锻锻的积极性，为本校九年级学生组织了一分钟跳绳比赛活动．王老师随机抽取了部分参赛学生的成绩，根据学生的成绩划分为A，B，C，D四个等级，将这组数据整理后制成统计图表．
根据图中提供的信息，回答下列问题：

(1)、抽取的学生共有　　人，并把条形图补充完整；

(2)、扇形统计图中，m＝；C等级对应扇形的圆心角为度；

(3)、学校想从获得D等级的学生中随机选取2人，参加市举办的跳绳比赛，请利用列表法或树形图法，求出D等级的小明参加市比赛的概率．

查看试题解析
15. “双减”政策受到各地教育部门的积极响应，某校为增加学生的课外活动时间，现决定增购两种体育器材：跳绳和毽子．已知跳绳的单价比毽子的单价多3元，用800元购买的跳绳个数和用500元购买的键子数量相同．

(1)、求跳绳和毽子的单价分别是多少元？

(2)、由于库存较大，商场决定对这两种器材打折销售，其中跳绳以八折出售，毽子以七折出售．学校计划购买跳绳和毽子两种器材共600个，且要求跳绳的数量不少于毽子数量的3倍，跳绳的数量不多于460根，请你求出学校花钱最少的购买方案．

查看试题解析
16. 为提高数学学习的兴趣，某学校数学社团利用周日举行了测量旗杆高度的活动．已知旗杆的底座高1米，长8米，宽6米，旗杆位于底座中心．
测量方法如下：在地面上找一点D，用测角仪测出看旗杆AB顶B的仰角为67.4°，沿DE方向走4.8米到达C地，再次测得看旗杆顶B的仰角为73.5°．

(1)、求旗杆的高度．

(2)、已知夏至日时该地的最大太阳高度约为78°，试问夏至日旗杆顶B的影子能不能落在台阶上？（太阳高度角是指某地太阳光线与地平线的夹角．结果精确到0.1m，参考数据：tan67.4°≈2.4，tan73.5°≈ $\frac{24}{7}$ ， tan22.6°≈ $\frac{5}{12}$ ， tan16.5°≈ $\frac{7}{24}$ ， tan12°≈0.21）

查看试题解析
17. 如图，点O是菱形ABCD的对角线的交点，DE∥AC，CE∥BD，连接OE．求证：

(1)、四边形OCED是矩形；

(2)、如果AB＝AC＝4，连接AE，求线段AE的长．

查看试题解析
18. △ABC是⊙O的内接三角形，点P是⊙O上一点，且点P与点A在BC的两侧，连接PA，PB，PC．

(1)、如图①，若△ABC是等边三角形，则线段PA，PB，PC之间有怎样的数量关系，并证明你的结论．

(2)、如图②，把（1）中的△ABC改为等腰直角三角形，∠BAC＝90°，其他条件不变，三条线段PA，PB，PC还有以上的数量关系吗？说明理由．

(3)、如图③，把（1）中△ABC改为任意三角形，AB＝c，AC＝b，BC＝a时，其他条件不变，则PA，PB，PC三条线段的数量关系为（直接写结果）

(4)、由以上你能发现圆内接四边形的四条边和对角线有什么关系？

查看试题解析
19. 已知：抛物线 $C_{1} ： y_{1} = - x^{2} + 4 x - 3$ 与x轴交于A、B两点，点A在点B左侧，将 $C_{1}$ 绕点A旋转180゜得到 $C_{2} ： y_{2} = a x^{2} + b x + c$ 交x轴与点N

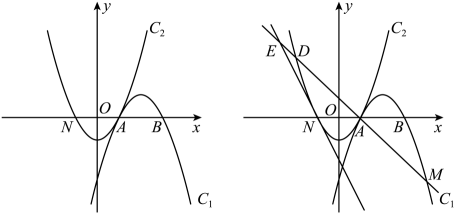(1)、求 $C_{2}$ 的解析式

(2)、求证：无论x取何值恒 $y_{1} \leq y_{2}$

(3)、当 $- x^{2} + 4 x - 3 \leq m x + n \leq a x^{2} + b x + c$ 时，求m和n的值．

(4)、直线 $l ： y = k x - 2$ 经过点N，D是抛物线 $c_{2}$ 上第二象限内的一点，设D的横坐标为q，作直线AD交抛物线 $c_{1}$ 于点M，交直线 $l$ 于点E，若DM＝2ED，求q值

查看试题解析

三、填空题

20. 已知|x+2y|+（x﹣4）²＝0，则xy＝．

查看试题解析
21. 竖直上抛物体时，物体离地而的高度 $h (m)$ 与运运动时间 $t (s)$ 之间的关系可以近似地用公式 $h = - 5 t^{2} + v_{0} t + h_{0}$ 表示，其中 $h_{0} (m)$ 是物体抛出时高地面的高度， $v_{0} (m / s)$ 是物体抛出时的速度．某人将一个小球从距地面 $1.5 m$ 的高处以 $20 m / s$ 的速度竖直向上抛出，小球达到的离地面的最大高度为m．

查看试题解析
22. 方程组 ${\begin{array}{l} 2 x + y = k \\ x - y = 8 k \end{array}$ 的解满足x＋2y＞14，则k的取值范围为

查看试题解析
23. ⊙P过坐标原点O，与x轴、y轴相交于点A、B，且OA＝OB＝4，反比例函数 $y = \frac{4}{x}$ 的图象经过圆点P，作射线OP，则图中阴影部分面积为

查看试题解析
24. 若直角三角形的两边长分别是一元二次方程x²－7x＋12＝0的两个实数根，则该直角三角形的面积是．

查看试题解析
25. 已知：点E是正方形ABCD边上的一点，将线段AE绕点E顺时针旋转90°，得到线段EA′，若AB＝2，则线段DA′的最小值为

查看试题解析