山东省德州市乐陵市2022年九年级第二次练兵考试数学试题
试卷更新日期:2022-05-31 类型:中考模拟
一、单选题
-
1. 2022的相反数为( )A、-2022 B、 C、±2022 D、20222. 下列图形中是轴对称图形但不是中心对称图形的是( )A、
 B、
B、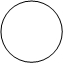 C、
C、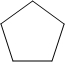 D、
D、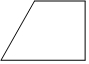 3. 清代·袁枚的一首诗《苔》中的诗句:“白日不到处,青春恰自来,苔花如米小,也学牡丹开.”若苔花的花粉直径约为0.0000084米,则数据0.0000084用科学记数法表示为( )A、 B、 C、 D、4. 某鞋店试销一种新款男鞋,试销期间销售情况如表,则该组数据的下列统计量中,对鞋店下次进货最具有参考意义的是( )
3. 清代·袁枚的一首诗《苔》中的诗句:“白日不到处,青春恰自来,苔花如米小,也学牡丹开.”若苔花的花粉直径约为0.0000084米,则数据0.0000084用科学记数法表示为( )A、 B、 C、 D、4. 某鞋店试销一种新款男鞋,试销期间销售情况如表,则该组数据的下列统计量中,对鞋店下次进货最具有参考意义的是( )鞋的尺码(cm)
24
24.5
25
25.5
26
26.5
销售数量(双)
2
7
18
10
8
3
A、中位数 B、平均数 C、方差 D、众数5. 下列运算正确的是( )A、 B、 C、 D、6. 如图,在平行四边形ABCD中,BD为对角线,下列结论正确的是( ) A、 B、 C、 D、与大小关系无法确定A7. 反比例函数的图象如图所示,则一次函数的图象大致是()
A、 B、 C、 D、与大小关系无法确定A7. 反比例函数的图象如图所示,则一次函数的图象大致是()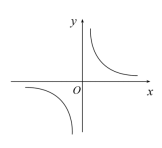 A、
A、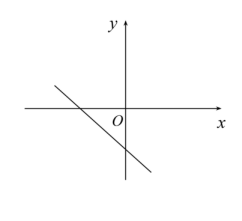 B、
B、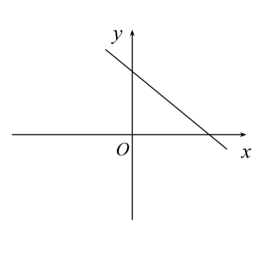 C、
C、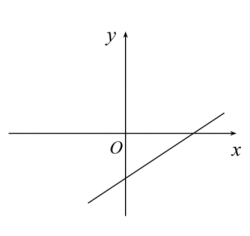 D、
D、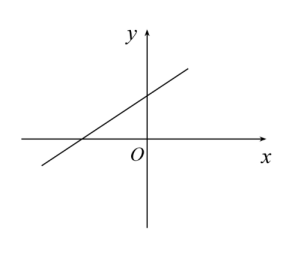 8. 如图,△ABC的顶点A,B在上,点C在外(O,C在AB同侧), , 则的度数可能是( )
8. 如图,△ABC的顶点A,B在上,点C在外(O,C在AB同侧), , 则的度数可能是( ) A、48° B、49° C、50° D、51°9. 某工程队在西城路改造一条长3000米的人行道,为尽量减少施工对交通造成的影响,施工时“×××”,设实际每天改造人行道x米,则可得方程 , 根据已有信息,题中用“×××”表示的缺失的条件应补充为( )A、每天比原计划少铺设10米,结果延迟15天完成 B、每天比原计划多铺设10米,结果延迟15天完成 C、每天比原计划少铺设10米,结果提前15天完成 D、每天比原计划多铺设10米,结果提前15天完成10. 如图,在Rt△ABC中, , , 分别以边A、B为圆心,大于的长为半径画弧,两弧分别交于F、G两点,连接F、G分别交于AB于E、BC于D,连接AD,若 , 则BC的长为( ).
A、48° B、49° C、50° D、51°9. 某工程队在西城路改造一条长3000米的人行道,为尽量减少施工对交通造成的影响,施工时“×××”,设实际每天改造人行道x米,则可得方程 , 根据已有信息,题中用“×××”表示的缺失的条件应补充为( )A、每天比原计划少铺设10米,结果延迟15天完成 B、每天比原计划多铺设10米,结果延迟15天完成 C、每天比原计划少铺设10米,结果提前15天完成 D、每天比原计划多铺设10米,结果提前15天完成10. 如图,在Rt△ABC中, , , 分别以边A、B为圆心,大于的长为半径画弧,两弧分别交于F、G两点,连接F、G分别交于AB于E、BC于D,连接AD,若 , 则BC的长为( ).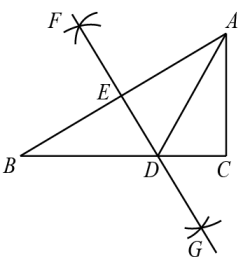 A、6 B、 C、9 D、11. 已知二次函数 , 图象上部分点的坐标(x,y)的对应值如下表所示,则方程的根是( )
A、6 B、 C、9 D、11. 已知二次函数 , 图象上部分点的坐标(x,y)的对应值如下表所示,则方程的根是( )x
…
0
4
…
y
…
0.37
-1
0.37
…
A、0或4 B、或4- C、1或5 D、无实根12. 如图,在正方形ABCD中,已知边长AB=5,点E是BC边上一动点(点E不与B、C重合),连接AE,作点B关于直线AE的对称点F,则线段CF的最小值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 因式分解: .
14. 已知点P(x+2,2x-3)在y轴上,则x= .15. 如果一个正六边形的周长等于12cm,那么这个正六边形的半径等于cm.16. 为落实好乐陵市“1115”高效课堂,李老师把班级里50名学生分成若干小组进行小组互助学习,每小组只能是4人或6人,则分组方案有种.17. 我们把宽与长的比为黄金比()的矩形称为黄金矩形,如图,在黄金矩形ABCD中, , BC=4,的平分线交AD边于点E,则AE的长为 . 18. 如图所示,将形状大小完全相同的“
18. 如图所示,将形状大小完全相同的“ ”按照一定规律摆成下列图形,第1幅图中“
”按照一定规律摆成下列图形,第1幅图中“ ”的个数为 , 第2幅图中“
”的个数为 , 第2幅图中“ ”的个数为 , 第3幅图中“
”的个数为 , 第3幅图中“ ”的个数为 , 以此类推,的值为 .
”的个数为 , 以此类推,的值为 . 
三、解答题
-
19. 先化简,再求值: , 其中 .20. 中考来临,同学们都进入了紧张的复习.为了了解九年级学生晚上睡眠时间的长短,数学组李老师对该校九年级学生进行了随机抽样调查,结果见右边的统计图,其中A代表睡眠9小时左右的人数,B代表睡眠8小时左右的人数,C代表睡眠7小时左右的人数,D代表睡眠6小时左右的人数,其中扇形“A”的圆心角为60°.
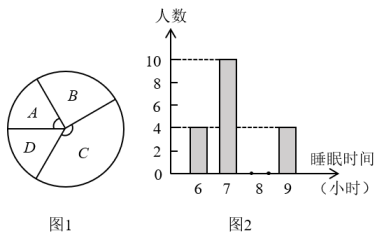 (1)、李老师一共调查了人,请你补全条形统计图;(2)、在扇形统计图中,扇形“C”的圆心角的度数为 .(3)、估计该校九年级学生每天的平均睡眠时间(保留一位小数);(4)、如果“D”中有1名男生,3名女生,现要从“D”中随机抽取两人到政教处去说说睡眠时间短的原因,那么恰好抽中一男一女的概率是多少?21. 如图为一种翻盖式圆柱形茶杯,底面直径为15cm,高为20cm.现将茶杯按照右图方式支在桌子上,当杯底倾斜到与桌面呈53°时,恰好将热水倒出.求此时杯子最高点A距离桌面的距离.(参考数据 , , )
(1)、李老师一共调查了人,请你补全条形统计图;(2)、在扇形统计图中,扇形“C”的圆心角的度数为 .(3)、估计该校九年级学生每天的平均睡眠时间(保留一位小数);(4)、如果“D”中有1名男生,3名女生,现要从“D”中随机抽取两人到政教处去说说睡眠时间短的原因,那么恰好抽中一男一女的概率是多少?21. 如图为一种翻盖式圆柱形茶杯,底面直径为15cm,高为20cm.现将茶杯按照右图方式支在桌子上,当杯底倾斜到与桌面呈53°时,恰好将热水倒出.求此时杯子最高点A距离桌面的距离.(参考数据 , , ) 22. 如图,AB=2,射线 , 点P为BM上一点,以BP为直径作 , 点D在上,AD=AB,连接PD,点Q为弦PD上一点,射线QC交于点E.
22. 如图,AB=2,射线 , 点P为BM上一点,以BP为直径作 , 点D在上,AD=AB,连接PD,点Q为弦PD上一点,射线QC交于点E. (1)、求证:AD为的切线;(2)、若 , 求劣弧的长.23. 现有一个文具袋,如图1所示,文具袋的上部分可以看成一个二次函数图象,下部分是矩形,文具袋的最大高度是13.5cm,底边长是22cm,矩形的宽是8cm.如图2,建立平面直角坐标系.
(1)、求证:AD为的切线;(2)、若 , 求劣弧的长.23. 现有一个文具袋,如图1所示,文具袋的上部分可以看成一个二次函数图象,下部分是矩形,文具袋的最大高度是13.5cm,底边长是22cm,矩形的宽是8cm.如图2,建立平面直角坐标系. (1)、求出该二次函数的表达式.(2)、某笔记本如图3的长和宽分别是20cm和10cm,试判断笔记本能不能放入文件袋中,请说明理由.24. 在学完菱形后,某教学兴趣小组尝试利用手中的数学工具——三角板和圆规作出一个内角为60°的菱形,下面是他们探究过程中的讨论片段,请仔细阅读,并完成相应的任务.
(1)、求出该二次函数的表达式.(2)、某笔记本如图3的长和宽分别是20cm和10cm,试判断笔记本能不能放入文件袋中,请说明理由.24. 在学完菱形后,某教学兴趣小组尝试利用手中的数学工具——三角板和圆规作出一个内角为60°的菱形,下面是他们探究过程中的讨论片段,请仔细阅读,并完成相应的任务.
小明:可以尝试利用含60°角的三角板和圆规作出菱形.如图①,将三角板ABC放置在图纸上、延长直角边BA,以点C为圆心、CA长为半径作弧,以点A为圆心、AC长为半径作弧,交BA的延长线于点E,交上弧于点D,连接CD,DE,则四边形ACDE即为所求作的菱形.小华:我可以在不利用三角板的前提下,作出符合要求的菱形.如图②,作半圆O及其直径AB、分到以点OB为圆心、大于的长为半径作弧,两弧交于点MN,作直线MN交半径圆O于点C;以点C为圆心、OC长为半径作弧,交半圆O于点D,连接AD,CD,CO,则四边形AOCD即为所作的菱形.
任务:
(1)、小明的做法中,判断四边形ACDE是菱形的依据可能是(填序号)①四条边都相等的四边形是菱形;②对角线互相垂直的四边形是菱形
③有一组邻边相等的平行四边形是菱形;④对角线互相垂直的平行四边形是菱形
(2)、请证明小明作出的图形四边形ACDE是菱形.(3)、你认为小华作出的四边形AOCD是有一个角为60°的菱形吗?请判断并说理由.(4)、如图③,小齐利用含45°角的三角板ABC和圆规构造了菱形ABMN,已知点P是线段MC上的一个点,AB=10,当时,请直接写出点P到直线MN的距离.25. 如图,在平面直角坐标系xOy中,一次函数y1=kx+b与反比例函数y2=(n>0)交于点A(-2,-1),B(1,m).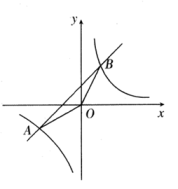 (1)、求 , 对应的函数表达式;(2)、直接写出当时,不等式的解集.(3)、求的面积;(4)、若点P是反比例函数图象上一点,且的面积是的面积的2倍,则点P的横坐标为 .
(1)、求 , 对应的函数表达式;(2)、直接写出当时,不等式的解集.(3)、求的面积;(4)、若点P是反比例函数图象上一点,且的面积是的面积的2倍,则点P的横坐标为 .