浙江省新昌天台临海三地2022届高三下学期数学5月适应性考试试卷
试卷更新日期:2022-05-31 类型:高考模拟
一、单选题
-
1. 设集合 , , 则( )A、{2} B、 C、 D、2. 若(i为虚数单位),则( )A、2 B、 C、4 D、3. 若x,y满足则的最大值为( )A、3 B、6 C、7 D、84. 某几何体的三视图(单位:)如图所示,则该几何体的体积(单位:)为( )
 A、4 B、6 C、12 D、155. 函数 的部分图象大致是( )A、
A、4 B、6 C、12 D、155. 函数 的部分图象大致是( )A、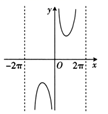 B、
B、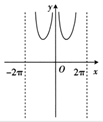 C、
C、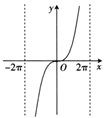 D、
D、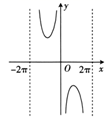 6. 设x是实数,则“”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件7. 已知分别为椭圆的左、右焦点,P为椭圆上一点,且垂直x轴,以为圆心的圆与直线相切于点T,则T的横坐标为( )A、 B、 C、 D、8. 已知正方体的棱长为3,E,F分别为棱上的动点.若直线与平面所成角为 , 则下列说法不正确的是( )
6. 设x是实数,则“”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件7. 已知分别为椭圆的左、右焦点,P为椭圆上一点,且垂直x轴,以为圆心的圆与直线相切于点T,则T的横坐标为( )A、 B、 C、 D、8. 已知正方体的棱长为3,E,F分别为棱上的动点.若直线与平面所成角为 , 则下列说法不正确的是( ) A、任意点E,F,二面角的大小为 B、任意点E,F,点C到面的距离为 C、存在点E,F,使得直线与所成角为 D、存在点E,F,使得线段长度为9. 已知 , 则的最大值是( )A、 B、 C、4 D、610. 已知等差数列满足 , 若 , 则k的最大值是( )A、8 B、9 C、10 D、11
A、任意点E,F,二面角的大小为 B、任意点E,F,点C到面的距离为 C、存在点E,F,使得直线与所成角为 D、存在点E,F,使得线段长度为9. 已知 , 则的最大值是( )A、 B、 C、4 D、610. 已知等差数列满足 , 若 , 则k的最大值是( )A、8 B、9 C、10 D、11二、填空题
-
11. “圆材埋壁”是我国古代著名数学著作《九章算术》中的一个问题:“今有圆材,埋于壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”此问题可以理解为“如果为圆O的直径,弦于E,寸,寸,那么直径的长为寸”.
 12. 如图,四边形中,且 , 则四边形面积取最大值时,.
12. 如图,四边形中,且 , 则四边形面积取最大值时,. 13. 已如平面向量两两都不共线.若 , 则的最大值是.14. 已知双曲线的一条渐近线为 , 则;离心率.15. 已知二项展开式 , 则;.16. 已知函数 , 则;若 , 则实数.17. 已知甲盒子里有3个球,其中1个红球,2个黑球;乙盒子里有5个球,其中3个红球,2个黑球.先从甲盒中取1个球,再从乙金中取2个球.设两次取球之后取到红球的总个数为 , 则;.
13. 已如平面向量两两都不共线.若 , 则的最大值是.14. 已知双曲线的一条渐近线为 , 则;离心率.15. 已知二项展开式 , 则;.16. 已知函数 , 则;若 , 则实数.17. 已知甲盒子里有3个球,其中1个红球,2个黑球;乙盒子里有5个球,其中3个红球,2个黑球.先从甲盒中取1个球,再从乙金中取2个球.设两次取球之后取到红球的总个数为 , 则;.三、解答题
-
18. 已知函数的部分图象如图所示,且的面积等于.
 (1)、求函数的单调递减区间;(2)、若 , 且 , 求的值.19. 在四棱锥中,侧面底面.
(1)、求函数的单调递减区间;(2)、若 , 且 , 求的值.19. 在四棱锥中,侧面底面. (1)、求证:;(2)、求直线与平面所成角的正弦值.
(1)、求证:;(2)、求直线与平面所成角的正弦值.
