广东省梅州市大埔县2021-2022学年九年级下学期期中数学试题
试卷更新日期:2022-05-30 类型:期中考试
一、单选题
-
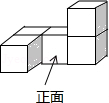
1. 的值是( )A、-2 B、-1 C、0 D、12. 如图是一个由5个完全相同的小正方体组成的立体图形,它的俯视图是( )
 A、
A、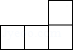 B、
B、 C、
C、 D、
D、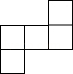 3. 2022年2月4日,冬奥会开幕式在全国44个卫星频道播出,总收视率20.1%,电视直播观众31600000人.将“31600000”用科学记数法表示为( )A、 B、 C、 D、4. 为更好地学习贯彻“2022年全国两会”精神,牢记使命担当,奋进新时代,筑梦新征程.某校举办了“2022年全国两会”知识竞赛,某班参赛的6名同学的成绩(单位:分)分别为:86,83,87,83,84,93,则这组数据的中位数是( )A、84 B、85 C、86 D、875. 下列运算正确的是( )A、 B、 C、 D、6. 《孙子算经》是中国古代重要的数学著作,成书于约一千五百年前,其中有首歌谣:今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?意即:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺,同时立一根一尺五寸的小标杆,它的影长五寸(提示:1丈=10尺,1尺=10寸),则竹竿的长为( )
3. 2022年2月4日,冬奥会开幕式在全国44个卫星频道播出,总收视率20.1%,电视直播观众31600000人.将“31600000”用科学记数法表示为( )A、 B、 C、 D、4. 为更好地学习贯彻“2022年全国两会”精神,牢记使命担当,奋进新时代,筑梦新征程.某校举办了“2022年全国两会”知识竞赛,某班参赛的6名同学的成绩(单位:分)分别为:86,83,87,83,84,93,则这组数据的中位数是( )A、84 B、85 C、86 D、875. 下列运算正确的是( )A、 B、 C、 D、6. 《孙子算经》是中国古代重要的数学著作,成书于约一千五百年前,其中有首歌谣:今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?意即:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺,同时立一根一尺五寸的小标杆,它的影长五寸(提示:1丈=10尺,1尺=10寸),则竹竿的长为( )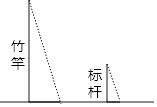 A、五丈 B、四丈五尺 C、一丈 D、五尺7. 已知的面积为16,点D,E分别为AB,AC边上的中点,则四边形DBCE的面积为( )A、12 B、10 C、9 D、88. 若 , 则( )A、11 B、1 C、-1 D、-119. 如图,直线MN是矩形ABCD的一条对称轴,点E在AD边E上,将沿BE折叠,使点A的对应点F落在直线MN上,若 , 则BE的长是( )
A、五丈 B、四丈五尺 C、一丈 D、五尺7. 已知的面积为16,点D,E分别为AB,AC边上的中点,则四边形DBCE的面积为( )A、12 B、10 C、9 D、88. 若 , 则( )A、11 B、1 C、-1 D、-119. 如图,直线MN是矩形ABCD的一条对称轴,点E在AD边E上,将沿BE折叠,使点A的对应点F落在直线MN上,若 , 则BE的长是( )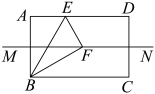 A、5 B、 C、 D、10. 如图,在Rt和Rt中, , , AB=AE=5.连接BD,CE,将△绕点A旋转一周,在旋转的过程中当最大时,△ACE的面积为( ).
A、5 B、 C、 D、10. 如图,在Rt和Rt中, , , AB=AE=5.连接BD,CE,将△绕点A旋转一周,在旋转的过程中当最大时,△ACE的面积为( ).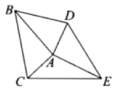 A、6 B、 C、9 D、
A、6 B、 C、9 D、二、填空题
-
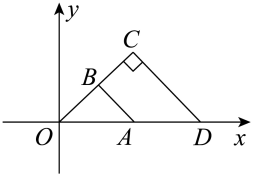
11. 分解因式: = .12. 在函数中,自变量x的取值范围是 .13. 在Rt△ABC中,∠C=90°,BC=5,AC=12,则sinB的值是.14. 写出一个开口向下,对称轴为直线的抛物线的解析式 .15. 如图,与是以点O为位似中心的位似图形,位似比为1∶2, , . 若 , 则点C的坐标为 .
 16. 如图,从一块直径是的圆形铁皮上剪出一个圆心角为90°的扇形,如果将剪下来的扇形围成一个圆锥,圆锥的底面圆的半径为m.
16. 如图,从一块直径是的圆形铁皮上剪出一个圆心角为90°的扇形,如果将剪下来的扇形围成一个圆锥,圆锥的底面圆的半径为m. 17. 已知关于x的函数 , , 若对于任意实数x,与的值至少有一个为正数.则实数a的取值范围是 .
17. 已知关于x的函数 , , 若对于任意实数x,与的值至少有一个为正数.则实数a的取值范围是 .三、解答题
-
18. 解方程:19. 如图,在中,点D,E,F分别在AB,AC,BC边上, , .
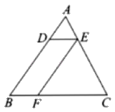 (1)、求证:;(2)、设 , , 求线段AB的长.20. 小王同学在超市进行随机抽样调查,了解人们平时喜欢用哪种方式付款,下图是根据调查结果整理出来的统计图,请据此信息完成下列问题:
(1)、求证:;(2)、设 , , 求线段AB的长.20. 小王同学在超市进行随机抽样调查,了解人们平时喜欢用哪种方式付款,下图是根据调查结果整理出来的统计图,请据此信息完成下列问题: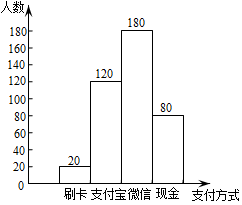 (1)、若当天该超市客流量为1.5万人,请你估计这一天使用微信支付的人数有多少人;(2)、现场调查也发现:甲、乙两人都习惯使用支付宝、微信、现金三种支付方式,并且他们选择这三种支付方式的可能性是相同的,请你利用列表或树状图计算出两人恰好选择同一种支付方式的概率.21. 如图,在中, .
(1)、若当天该超市客流量为1.5万人,请你估计这一天使用微信支付的人数有多少人;(2)、现场调查也发现:甲、乙两人都习惯使用支付宝、微信、现金三种支付方式,并且他们选择这三种支付方式的可能性是相同的,请你利用列表或树状图计算出两人恰好选择同一种支付方式的概率.21. 如图,在中, . (1)、尺规作图:以AB为直径作⊙O分别交BC,AC于点D,E,连接EB,OD(保留作图痕迹,不写作法);(2)、求证: .22. 小明的爸爸出差回家后,小明发现爸爸的通信大数据行程卡上显示14天内爸爸去过深圳、广州、湛江.已知广州到深圳的路程比广州到湛江的路程少280公里,小明的爸爸驾车从深圳到广州的平均速度是70千米/小时,从广州到湛江的平均速度是60千米/小时,从广州到湛江的时间比从深圳到广州的时间多5小时.(1)、求广州到深圳的路程;(2)、从广州到湛江时,若小明的爸爸要至少提前2小时到家.则驾车的平均速度应满足什么条件?23. 如图,已知二次函数的图象与x轴交于点A,点B,与y轴交于点C,其顶点为D,直线DC的函数解析式为 . 已知
(1)、尺规作图:以AB为直径作⊙O分别交BC,AC于点D,E,连接EB,OD(保留作图痕迹,不写作法);(2)、求证: .22. 小明的爸爸出差回家后,小明发现爸爸的通信大数据行程卡上显示14天内爸爸去过深圳、广州、湛江.已知广州到深圳的路程比广州到湛江的路程少280公里,小明的爸爸驾车从深圳到广州的平均速度是70千米/小时,从广州到湛江的平均速度是60千米/小时,从广州到湛江的时间比从深圳到广州的时间多5小时.(1)、求广州到深圳的路程;(2)、从广州到湛江时,若小明的爸爸要至少提前2小时到家.则驾车的平均速度应满足什么条件?23. 如图,已知二次函数的图象与x轴交于点A,点B,与y轴交于点C,其顶点为D,直线DC的函数解析式为 . 已知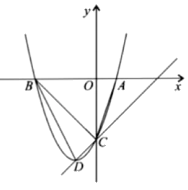 (1)、求二次函数的函数解析式和直线DC的函数解析式;(2)、连接BD,求的面积.24. 如图
(1)、求二次函数的函数解析式和直线DC的函数解析式;(2)、连接BD,求的面积.24. 如图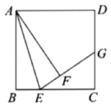 (1)、问题探究:如图,已知正方形ABCD中.点E是BC边上一动点,将沿着AE对折后,点B落在点F处,延长EF交CD于点G.求证:;(2)、问题解决:在(1)的条件下,的值是否为定值,若是,请求出该定值;若不是,请说明理由.25. 如图,在四边形ABCD中, . . , , . 点P从点A沿AD运动到点D,每秒移动a个单位,同时点Q从点C沿CB运动到点B.每秒移动b个单位.运动时间为x秒.若其中一点到达终点,另一点也停止.
(1)、问题探究:如图,已知正方形ABCD中.点E是BC边上一动点,将沿着AE对折后,点B落在点F处,延长EF交CD于点G.求证:;(2)、问题解决:在(1)的条件下,的值是否为定值,若是,请求出该定值;若不是,请说明理由.25. 如图,在四边形ABCD中, . . , , . 点P从点A沿AD运动到点D,每秒移动a个单位,同时点Q从点C沿CB运动到点B.每秒移动b个单位.运动时间为x秒.若其中一点到达终点,另一点也停止.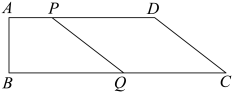 (1)、请求出CD的值;(2)、若存在某时刻使DQ垂直平分PC,求a∶b的值;(3)、若 , , 何时PQ上存在点M,使得 .
(1)、请求出CD的值;(2)、若存在某时刻使DQ垂直平分PC,求a∶b的值;(3)、若 , , 何时PQ上存在点M,使得 .