黑龙江省佳木斯市2022年中考一模数学试题

试卷更新日期：2022-05-30 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列运算正确的是（）

A、 $\sqrt{4} = \pm 2$ B、 $m^{3} + 2 m^{3} = 3 m^{3}$ C、 $m^{2} \cdot m^{3} = m^{6}$ D、 ${(- 2 m^{3})}^{2} = - 4 m^{6}$

查看试题解析
2. 下列图形中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 如图所示的几何体是由五个小正方体组合而成的，它的左视图是（）

A、 B、 C、 D、

查看试题解析
4. 已知数据91，94，94，95，97，99，将这组数据都减去91得到一组新的数据，则这两组数据下列统计量相同的是（）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
5. 某校八年级组织篮球赛，若每两班之间赛一场，共进行了28场，则该校八年级有（　　）个班级．

A、8 B、9 C、10 D、11

查看试题解析
6. 已知分式方程 $\frac{2 x + 3}{x + 1} = \frac{k}{x^{2} + 2 x + 1} + 2$ 的解为负数，则k的取值范围是（）

A、 $k > 1$ B、 $k > 1$ 且 $k \neq - 1$ C、 $k < 1$ D、 $k < 1$ 且 $k \neq 0$

查看试题解析
7. 为了奖励学习认真的同学，班主任老师给班长拿了40元钱，让其购买奖品，现有单价为4元的A种学习用品和单价为6元的B种学习用品可供选择，若40元钱恰好花完，则班长的购买方案有（）

A、1种 B、2种 C、3种 D、4种

查看试题解析
8. 如图，在平面直角坐标系中，菱形OABC的顶点A的坐标为 $(- 5 ， 0)$ ，对角线AC，BO相交于点D，双曲线 $y = \frac{k}{x} (x < 0)$ 经过点D， $A C + O B = 6 \sqrt{5}$ ， k的值为（）

A、-32 B、-36 C、-8 D、=4

查看试题解析
9. 如图，在 $△ A B C$ 中， $C E$ 是中线， $C D$ 是角平分线， $A F ⊥ C D$ 交 $C D$ 延长线于点 $F$ ， $A C = 7$ ， $B C = 4$ ，则 $E F$ 的长为（）

A、1.5 B、2 C、2.5 D、3

查看试题解析
10. 如图，在正方形ABCD中，M，N分别是AB，CD的中点，P是线段MN上的一点，BP的延长线交AD于点E，连接PD，PC，将 $△ D E P$ 绕点P顺时针旋转 $90 °$ 得 $△ G F P$ ，则下列结论：① $C P = G P$ ；② $t a n ∠ C G F = 1$ ；③BC垂直平分FG；④若 $A B = 4$ ，点E在AD边上运动，则D，F两点之间距离的最小值是 $\frac{3}{2} \sqrt{2}$ ．其中结论正确的序号有（）

A、②③ B、①②③ C、①②④ D、①③④

查看试题解析

二、填空题

11. 人的血管首尾相连的长度大约可达96000千米，96000千米用科学记数法表示为米.

查看试题解析
12. 函数y= $\frac{1}{x - 3}$ 中自变量x的取值范围是．

查看试题解析
13. 如图，点A，F，C，D在同一条直线上， $A F = D C$ ， $∠ 1 = ∠ 2$ ，请你再添加一个条件使 $△ A B C ≌ △ D E F$ ．你添加的条件是．

查看试题解析
14. 小明和小亮在玩“石头、剪子、布”的游戏，两人一起做同样手势的概率是．

查看试题解析
15. 若关于x的一元一次不等式组 ${\begin{array}{l} x - a > 0 \\ 2 x - 2 < 1 - x \end{array}$ 有解，则a的取值范围是．

查看试题解析
16. 如图，半径为2的 $⊙ O$ 是 $△ A B C$ 的外接圆， $∠ B A C = 30 °$ ，则弦BC的长等于．

查看试题解析
17. 圆锥的底面半径为3，侧面积为21π，则这个圆锥的高为．

查看试题解析
18. 如图，在 $R t △ A B C$ 中， $∠ A B C = 90 °$ ， $B C = 3$ ， $A B = 4$ ， M，N分别是AB，BC上的一点，且 $M N = 3$ ， O是MN的中点，G是AC上的任一点，连接OB，OG，则 $O B + O G$ 的最小值为．

查看试题解析
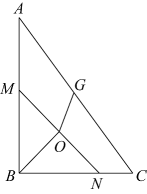19. 在矩形ABCD中， $B C = 4$ ， E为AD的中点，点F在射线AB上， $B F = 3$ ，过点E作 $E G ⊥ C F$ 于点G，EF平分 $∠ A E G$ ，则AB的长为．

查看试题解析
20. 如图， $△ O A A_{1}$ 是直角边长为2的等腰直角三角形，以等腰直角三角形 $O A A_{1}$ 的斜边 $O A_{1}$ 为直角边作第二个等腰直角三角形 $O A_{1} A_{2}$ ，连接 $A A_{2}$ ，得到 $△ A A_{1} A_{2}$ ；再以等腰直角三角形 $O A_{1} A_{2}$ 的斜边 $O A_{2}$ 为直角边作第三个等腰直角三角形 $O A_{2} A_{3}$ ，连接 $A_{1} A_{3}$ ，得到 $△ A_{1} A_{2} A_{3}$ ；再以等腰直角三角形 $△ O A_{2} A_{3}$ 的斜边 $O A_{3}$ 为直角边作第四个等腰直角三角形 $O A_{3} A_{4}$ ，连接 $A_{2} A_{4}$ ，得到 $△ A_{2} A_{3} A_{4}$ ， …记 $△ A A_{1} A_{2} ， △ A_{1} A_{2} A_{3} ， △ A_{2} A_{3} A_{4}$ …的面积分别为 $S_{1} ， S_{2} ， S_{3} ，$ …，如此下去，则 $S_{2022} =$ ．

查看试题解析

三、解答题

21. 先化简，再求值： $(\frac{x + 2}{x - 2} - \frac{x^{2} - 2 x}{x^{2} - 4 x + 4}) \div \frac{x - 4}{x - 2}$ ，其中 $x = 4 t a n 45 ° + 2 s i n 60 °$ ．

查看试题解析
22. 如图，平面直角坐标系内， $△ A B C$ 的顶点A的坐标为 $(- 3 ， 4)$ ．
⑴画出 $△$ 关于y轴的对称图形 $△ A_{1} B_{1} C_{1}$ ；
⑵画出将 $△ A B C$ 绕原点O逆时针旋转 $90 °$ 得到的 $△ A_{2} B_{2} C_{2}$ ；
⑶求出（2）中点A所经过的路径长．

查看试题解析
23. 如图，抛物线 $y = a x^{2} + b x + 3$ 与x轴交于点 $A (- 3 ， 0)$ 和点 $B (- 1 ， 0)$ ．

(1)、求抛物线的解析式；

(2)、将抛物线沿x轴向右平移t个单位长度，使它经过点 $(0 ， 1)$ ，求出t的值．

查看试题解析
24. 目前“微信”“支付宝”“共享单车”和“网购”给我们的生活带来了很多便利，九年级数学小组在校内对“你最认可的新生事物”进行调查，随机调查了m名学生（每名学生必选一种且只能从这四种中选择一种），并将调查结果绘制成如图所示不完整的统计图．

(1)、根据图中信息，求出m= ， n=；

(2)、请把条形统计图补充完整；

(3)、根锯抽样调查的结果，请估算在全校1800名学生中，最认可“微信”和“支付宝”这两样新生事物的学生共有多少名．

查看试题解析
25. 货车和轿车分别从甲、乙两地同时出发，沿同一公路相向而行．轿车出发 $2.4 h$ 后休息，直至与货车相遇后，以原速度继续行驶，设两车出发时间为x（单位：h），货车、轿车与甲地的距离为 $y_{1}$ （单位： $k m$ ）， $y_{2}$ （单位： $k m$ ），图中的线段OA、折线BCDE分别表示 $y_{1} ， y_{2}$ 与x之间的函数关系．

(1)、货车行驶的速度为 $k m / h$ ；

(2)、求DE所在直线的函数解析式；

(3)、直接写出两车出发多长时间相距 $200 k m$ ．

查看试题解析
26. 在等腰三角形ABC中，顶角 $∠ B A C = α$ ， D是CA延长线上一点，连接DB，将线段DB绕点D逆时针旋转，旋转角为 $α$ ，得到线段DE，连接CE，BE．

(1)、如图①，当 $α = 60 °$ 时，线段AD与CE的数量关系是；

(2)、如图②，当 $α = 90 °$ 时，线段AD与CE有怎样的数量关系？写出你的猜想，并给予证明；

(3)、如图③，当 $α = 120 °$ 时，线段AD与CE有怎样的数量关系？写出你的猜想，不必证明．

查看试题解析
27. 某商店决定购进 $A$ ､ $B$ 两种纪念品．若购进 $A$ 种纪念品8件， $B$ 种纪念品3件，需要95元；若购进 $A$ 种纪念品5件， $B$ 种纪念品6件，需要80元．

(1)、求购进 $A$ ､ $B$ 两种纪念品每件各需多少元？

(2)、若该商店决定购进这两种纪念品共100件，考虑市场需求和资金周转，用于购买这100件纪念品的资金不少于750元，但不超过764元，那么该商店有哪几种进货方案？

(3)、已知商家出售一件 $A$ 种纪念品可获利5元，出售一件 $B$ 种纪念品可获利3元，若商品全部卖出，试问在（2）的条件下，商家采用哪种方案可获利最多，最多为多少元？（直接写出结果，不说明理由）

查看试题解析
28. 如图，在平面直角坐标系中，直线AB交y轴于点A，交x轴于点B，OA，OB（ $O A < O B$ ）的长是关于x的一元二次方程 $x^{2} - 7 x + 12 = 0$ 的两个根，直线 $x = 2$ 交AB于点D，交x轴于点E，P是直线 $x = 2$ 上一动点，设 $P (2 ， n)$ ．

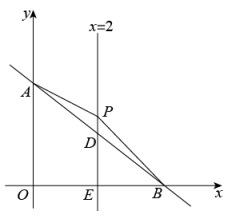(1)、求直线AB的解析式；

(2)、设 $△ A B P$ 的面积为S（ $S \neq 0$ ），求S关于n的函数关系式，并写出自变量n的取值范围；

(3)、在（2）的条件下，当 $S = 1$ ，且点P在AB上方时，在第一象限是否存在点C，使 $△ P B C$ 是等腰直角三角形？若存在，请直接写出点C的坐标；若不存在，请说明理由．

查看试题解析