黑龙江省佳木斯市前进区2022年九年级第二次模拟考试数学试题
试卷更新日期:2022-05-30 类型:中考模拟
一、填空题
-
1. 2022年2月8日,中国运动员谷爱凌在自由式滑雪女子大跳台决赛中夺冠,这是北京冬奥会中中国队在雪上项目中夺得的首枚金牌,滑雪大跳台项目场馆,坐落在北京市首钢园区的北京冬季奥林匹克公园,园区总占地面积171.2公顷即1712000平方米,将1712000用科学记数法表示为 .2. 函数y=中自变量x的取值范围是.3. 如图,四边形为平行四边形,延长至 , 使 , 连接 , , , 若添加一个条件后,使四边形成为矩形,则添加的条件是 .
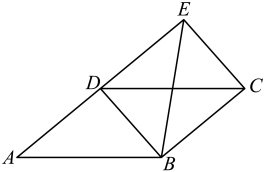 4. 小亮是个集邮爱好者,他收集了如图所示的四张纪念邮票(除正面内容不同外,其余均相同),小亮从中随机抽取一张邮票(不放回),再从余下的邮票中随机抽取一张,抽到的两张邮票恰好是“冬奥会会徽”和“冬奥会吉祥物冰墩墩”的概率是 .
4. 小亮是个集邮爱好者,他收集了如图所示的四张纪念邮票(除正面内容不同外,其余均相同),小亮从中随机抽取一张邮票(不放回),再从余下的邮票中随机抽取一张,抽到的两张邮票恰好是“冬奥会会徽”和“冬奥会吉祥物冰墩墩”的概率是 . 5. 关于的不等式组只有一个解,则与的关系是 .6. 如图,是⊙的直径,是⊙的弦,连结 , . 若 , , 则 .
5. 关于的不等式组只有一个解,则与的关系是 .6. 如图,是⊙的直径,是⊙的弦,连结 , . 若 , , 则 . 7. 若圆锥的底面半径为5,高为12,则圆锥的侧面展开图的面积是.8. 已知菱形中, , . 点、、分别为、、上的动点,则的最小值是 .
7. 若圆锥的底面半径为5,高为12,则圆锥的侧面展开图的面积是.8. 已知菱形中, , . 点、、分别为、、上的动点,则的最小值是 . 9. 如图,在矩形中, , , 点为边上任意一点,将沿折叠,使点落在点处,连接 , 若是直角三角形,则线段的长为 .
9. 如图,在矩形中, , , 点为边上任意一点,将沿折叠,使点落在点处,连接 , 若是直角三角形,则线段的长为 . 10. 如图,正方形的边长为1,正方形的边长为2,正方形的边长为4,正方形的边长为8…依次规律继续作正方形 , 且点 , , , , …,在同一条直线上,连接交,于点 , 连接 , 交于点 , 连接 , 交于点 , …记四边形的面积为 , 四边形的面积为 , 四边形的面积为 , …,四边形的面积为 , 则 .
10. 如图,正方形的边长为1,正方形的边长为2,正方形的边长为4,正方形的边长为8…依次规律继续作正方形 , 且点 , , , , …,在同一条直线上,连接交,于点 , 连接 , 交于点 , 连接 , 交于点 , …记四边形的面积为 , 四边形的面积为 , 四边形的面积为 , …,四边形的面积为 , 则 .
二、单选题
-
11. 下列运算正确的是( )A、 B、 C、 D、12. 第二十四届冬季奥林匹克运动会将于2022年在北京举行,北京将成为历史上第一座既举办过夏奥会,又举办过冬奥会的城市.下面的图形是各届冬奥会会徽中的部分图案,其中是轴对称图形,但不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 13. 如图,在下面四种用相同的正方体储物箱堆放在一起的形态中,从正面看到的和从左面看到的图形不相同的是( )A、
13. 如图,在下面四种用相同的正方体储物箱堆放在一起的形态中,从正面看到的和从左面看到的图形不相同的是( )A、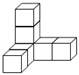 B、
B、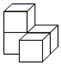 C、
C、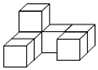 D、
D、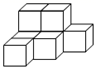 14. 某运动员为备战南京青奥会,刻苦进行训练,为了判断他的成绩是否稳定,教练对他近阶段10次训练的成绩进行统计和分析,那么教练最需要了解该运动员这10次成绩的( )A、众数 B、方差 C、平均数 D、中位数15. 新型冠状病毒肺炎具有人传人性,调查发现1人感染病毒后如果不隔离,那么经过两轮传染将会有225人感染,若设1人平均感染x人,则x为( )A、14 B、15 C、16 D、1716. 若关于x的分式方程的解为正数,则m的取值范围是( ).A、m<-2且 B、m<2且 C、m>-3且 D、m>-3且17. 如图,过双曲线上的动点作轴于点 , 是直线上的点,且满足 , 过点作轴的平行线交此双曲线于点 . 如果的面积为8,则的值为( )
14. 某运动员为备战南京青奥会,刻苦进行训练,为了判断他的成绩是否稳定,教练对他近阶段10次训练的成绩进行统计和分析,那么教练最需要了解该运动员这10次成绩的( )A、众数 B、方差 C、平均数 D、中位数15. 新型冠状病毒肺炎具有人传人性,调查发现1人感染病毒后如果不隔离,那么经过两轮传染将会有225人感染,若设1人平均感染x人,则x为( )A、14 B、15 C、16 D、1716. 若关于x的分式方程的解为正数,则m的取值范围是( ).A、m<-2且 B、m<2且 C、m>-3且 D、m>-3且17. 如图,过双曲线上的动点作轴于点 , 是直线上的点,且满足 , 过点作轴的平行线交此双曲线于点 . 如果的面积为8,则的值为( ) A、10 B、8 C、16 D、1218. 新冠状病毒传染性非常强,多是通过飞沫,接触,还有气溶胶传播。所以一定要做好个人防护,尽量少外出,更不要聚集,佩戴医用外科口罩是非常有效的个人防护。为了个人防护,小红用40元钱买了A,B两种型号的医用外科口罩(两种型号都买),A型每包6元,B型每包4元,在40元全部用尽的情况下,有几种购买方案( )A、2种 B、3种 C、4种 D、5种19. 如图,已知平行四边形的面积为 , 为的中点,连接 , 则的面积为( )
A、10 B、8 C、16 D、1218. 新冠状病毒传染性非常强,多是通过飞沫,接触,还有气溶胶传播。所以一定要做好个人防护,尽量少外出,更不要聚集,佩戴医用外科口罩是非常有效的个人防护。为了个人防护,小红用40元钱买了A,B两种型号的医用外科口罩(两种型号都买),A型每包6元,B型每包4元,在40元全部用尽的情况下,有几种购买方案( )A、2种 B、3种 C、4种 D、5种19. 如图,已知平行四边形的面积为 , 为的中点,连接 , 则的面积为( ) A、 B、 C、 D、20. 如图,正方形的边长为2,点从点出发沿着线段向点运动(不与点、重合),同时点从点出发沿着线段向点运动(不与点、重合),点与点的运动速度相同.与相交于点 , 为中点,则有下列结论:①是定值;②平分;③当运动到中点时,;④当时,四边形的面积是 . 其中正确的是( )
A、 B、 C、 D、20. 如图,正方形的边长为2,点从点出发沿着线段向点运动(不与点、重合),同时点从点出发沿着线段向点运动(不与点、重合),点与点的运动速度相同.与相交于点 , 为中点,则有下列结论:①是定值;②平分;③当运动到中点时,;④当时,四边形的面积是 . 其中正确的是( ) A、①③ B、①②③ C、①③④ D、①④
A、①③ B、①②③ C、①③④ D、①④三、解答题
-
21. 先化简,再求代数式()÷的值,其a=2cos30°+tan45°.22. 如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中,△ABC的三个顶点A(5,2)、B(5,5)、C(1,1)均在格点上.
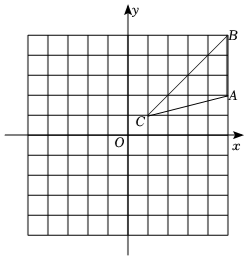 (1)、画出△ABC向左平移5个单位后的图形△A1B1C1 , 则A1点的坐标为 ▲ .(2)、画出△A1B1C1绕C1顺时针旋转90°后的图形△A2B2C1 , 则A2点的坐标为 ▲ .(3)、在(2)的条件下,求△A1B1C1扫过的面积.23. 如图,已知抛物线经过点 , 及原点 , 顶点为 .
(1)、画出△ABC向左平移5个单位后的图形△A1B1C1 , 则A1点的坐标为 ▲ .(2)、画出△A1B1C1绕C1顺时针旋转90°后的图形△A2B2C1 , 则A2点的坐标为 ▲ .(3)、在(2)的条件下,求△A1B1C1扫过的面积.23. 如图,已知抛物线经过点 , 及原点 , 顶点为 . (1)、求抛物线的函数解析式;(2)、连接交轴于点 . 连接 , . 试在轴负半轴上找一点 , 使得与相似.请直接写出点的坐标.24. 在“双减”和“双增”的政策下,某校七年级开设了五门手工课,按照类别分别为: . 剪纸; . 沙画; . 雕刻; . 泥塑; . 插花,每个学生仅限选择一项,为了了解学生对每种手工课的喜爱程度,随机抽取了七年级部分学生进行调查,并将调查结果绘制成如下两幅不完整的统计图:
(1)、求抛物线的函数解析式;(2)、连接交轴于点 . 连接 , . 试在轴负半轴上找一点 , 使得与相似.请直接写出点的坐标.24. 在“双减”和“双增”的政策下,某校七年级开设了五门手工课,按照类别分别为: . 剪纸; . 沙画; . 雕刻; . 泥塑; . 插花,每个学生仅限选择一项,为了了解学生对每种手工课的喜爱程度,随机抽取了七年级部分学生进行调查,并将调查结果绘制成如下两幅不完整的统计图:
根据统计图提供的信息,解答下列问题:
(1)、本次共调查了名学生;扇形统计图中 , 类别所对应的扇形圆心角的度数是度;(2)、请根据以上信息直接补全条形统计图;(3)、在学期结束时,从开设的五门手工课中各选出一名学生谈感悟,由于这五名同学采用随机抽签的方式确定顺序,请用树状图或列表的方式说明剪纸()和雕刻()两人排在前两位谈感受的概率.25. 甲、乙两地相距200千米,货车从甲地出发,行驶1小时后在途中的丙地出现故障,技术人员乘轿车以100千米/小时的速度从甲地赶来维修(沟通时间忽略不计).到达丙地修好车后以原速原路返回,同时货车改变速度前往乙地.两车距乙地的路程 (千米)与货车驶时间 (小时)之间的函数关系如图所示,请结合图象回答下列问题. (1)、货车出现故障前后的速度分别为、千米/小时;(2)、货车在丙地停留了小时;(3)、求图中线段 的函数关系式:(4)、轿车出发后,又过了小时,两车相距路程为40千米.26. 已知∠ABC=60°,点F在直线BC上,以AF为边作等边三角形AFE,过点E作ED⊥AB于点D.请解答下列问题:
(1)、货车出现故障前后的速度分别为、千米/小时;(2)、货车在丙地停留了小时;(3)、求图中线段 的函数关系式:(4)、轿车出发后,又过了小时,两车相距路程为40千米.26. 已知∠ABC=60°,点F在直线BC上,以AF为边作等边三角形AFE,过点E作ED⊥AB于点D.请解答下列问题: (1)、如图①,求证:AB+BF=2BD;(2)、如图②、图③,线段AB,BF,BD又有怎样的数量关系?请写出你的猜想,不需要证明.27. 第二十四届冬季奥林匹克运动会于2022年2月20日在北京圆满闭幕,目前冰墩墩和雪容融吉祥物在市场热销.某特许商店准备购进冰墩墩和雪容融吉祥物若干,其进价和售价如下表:
(1)、如图①,求证:AB+BF=2BD;(2)、如图②、图③,线段AB,BF,BD又有怎样的数量关系?请写出你的猜想,不需要证明.27. 第二十四届冬季奥林匹克运动会于2022年2月20日在北京圆满闭幕,目前冰墩墩和雪容融吉祥物在市场热销.某特许商店准备购进冰墩墩和雪容融吉祥物若干,其进价和售价如下表:冰墩墩吉祥物
雪容融吉祥物
进价(元/件)
m
m﹣30
售价(元/件)
300
200
已知用3000元购进冰墩墩吉祥物的数量与用2400元购进雪容融吉祥物的数量相同.
(1)、求m的值;(2)、要使购进的两种吉祥物共200件的总利润(利润=售价﹣进价)不少于21700元,且不超过22300元,该商店有几种进货方案?(3)、在(2)的条件下,该商店准备对冰墩墩吉祥物每件优惠a元进行出售,雪容融吉祥物的售价不变,该商店怎样进货才能获得最大利润?28. 在平面直角坐标系中的位置如图所示,与轴交于点 , 点的坐标为 , 线段 , 的长分别是方程的两根, . (1)、求线段的长;(2)、动点从点出发,以每秒1个单位长度的速度沿轴负半轴向终点运动,过点作直线与轴垂直,设点运动的时间为秒,直线扫过四边形的面积为 , 求与的关系式;(3)、为直线上一点,在平面内是否存在点 , 使以 , , , 为顶点的四边形为正方形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
(1)、求线段的长;(2)、动点从点出发,以每秒1个单位长度的速度沿轴负半轴向终点运动,过点作直线与轴垂直,设点运动的时间为秒,直线扫过四边形的面积为 , 求与的关系式;(3)、为直线上一点,在平面内是否存在点 , 使以 , , , 为顶点的四边形为正方形?若存在,请直接写出点N的坐标;若不存在,请说明理由.