黑龙江省哈尔滨市香坊区2022年九年级下学期二模数学试卷

试卷更新日期：2022-05-30 类型：中考模拟

进入出卷网下载

一、单选题

1. 某日的最高气温为32℃，最低气温为24℃，则这天的最高气温比最低气温高（）

A、 $- 8 ℃$ B、 $- 6 ℃$ C、8℃ D、10℃

查看试题解析
2. 下列运算正确的是（）

A、 $a^{10} \div a^{5} = a^{2}$ B、 ${(x - y)}^{2} = x^{2} - y^{2}$ C、 $4 a^{3} \cdot (- 3 a^{3}) = - 12 a^{6}$ D、 ${(a^{3})}^{4} = a^{7}$

查看试题解析
3. 如图所示的几何体是由七个相同的小正方体组合而成的，它的俯视图是（）

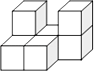A、 B、 C、 D、

查看试题解析
4.
如图，滑雪场有一坡角α为20°的滑雪道，滑雪道AC的长为200米，则滑雪道的坡顶到坡底垂直高度AB的长为（　　）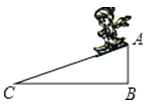

A、200tan20°米 B、 $\frac{200}{\sin 20 °}$ 米 C、200sin20°米 D、200cos20°米

查看试题解析
5. 抛物线 $y = - 2 {(x - 1)}^{2} + 8$ 的顶点坐标是（）

A、 $(1 ， 8)$ B、 $(- 1 ， 8)$ C、 $(- 1 ， - 8)$ D、 $(1 ， - 8)$

查看试题解析
6. 某车间有26名工人，每人每天可以生产800个螺钉或1000个螺母，1个螺钉需要配2个螺母，为使每天生产的螺钉和螺母刚好配套．设安排 $x$ 名工人生产螺母，则下列方程正确的是（）

A、 $2 \times 1000 (26 - x) = 800 x$ B、 $2 \times 800 (26 - x) = 1000 x$ C、 $1000 (26 - x) = 2 \times 800 x$ D、 $800 (26 - x) = 2 \times 1000 x$

查看试题解析
7. 如图， $Δ A B C$ 中， $∠ B A C = 90 °$ ，将 $Δ A B C$ 绕着点 $A$ 旋转至 $Δ A D E$ ，点 $B$ 的对应点点 $D$ 恰好落在 $B C$ 边上．若 $A C = 2 \sqrt{3}$ ， $∠ B = 60 °$ ，则 $C D$ 的长为（）

A、2 B、3 C、 $2 \sqrt{3}$ D、4

查看试题解析
8. 反比例函数 $y = \frac{k - 2}{x}$ 的图象，当x＞0时，y随x的值增大而增大，则k的取值范围是（）

A、k＜2 B、k≤2 C、k＞2 D、k≥2

查看试题解析
9. 如图，点F是▱ABCD的边CD上一点，直线BF交AD的延长线于点E，则下列结论错误的是（）

A、 $\frac{E D}{E A} = \frac{D F}{A B}$ B、 $\frac{E D}{B C} = \frac{E F}{F B}$ C、 $\frac{B C}{D E} = \frac{B F}{B E}$ D、 $\frac{B F}{B E} = \frac{B C}{A E}$

查看试题解析
10. 甲、乙两车同时从A地出发，沿同一路线各自匀速向B地行驶，甲到达B地停留1小时后按原路以另一速度匀速返回，直到与乙车相遇.乙车的速度为每小时60千米.两车之间的距离y（千米）与乙车行驶时间x（小时）之间的函数图象如图所示，则下列结论错误的是（）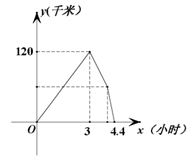

A、行驶3小时后，两车相距120千米 B、甲车从A到B的速度为100千米/小时 C、甲车返回是行驶的速度为95千米/小时 D、A，B两地之间的距离为300千米

查看试题解析

二、填空题

11. 某企业利用太阳能发电，年发电量可达2840000度.2840 000用科学记数法可表示为.

查看试题解析
12. 函数y＝ $\frac{2}{x - 3}$ 的自变量x的取值范围是.

查看试题解析
13. 把多项式 $x^{3} - 2 x^{2} y + x y^{2}$ 分解因式的结果是．

查看试题解析
14. 计算 $\sqrt{45} - \frac{\sqrt{20}}{2}$ 的结果是．

查看试题解析
15. 如果弧长为 $4 π c m$ 的扇形面积为 $16 π c m^{2}$ ，那么该扇形的半径为cm．

查看试题解析
16. 不等式组 ${\begin{array}{l} 3 x + 2 ＞ 2 x \\ - (x - 4) \geq 1 \end{array}$ 的解集为．

查看试题解析
17. 如图， $B A$ 为 $⊙ O$ 的切线，切点为点 $A$ ， $B O$ 交 $⊙ O$ 于点 $C$ ，点 $D$ 在 $⊙ O$ 上，连接 $C D$ ， $∠ A B O = 36 °$ ，则 $∠ A D C =$ ．

查看试题解析
18. 一个布袋里装有2个红球，1个白球，每个球除颜色外均相同，从中任意模出一个球，记下颜色并放回，再摸出一个球，则两次摸出的球都是红球的概率是．

查看试题解析
19. 已知等腰 $△ A B C$ 中， $A B = A C$ ， $B D ⊥ A C$ ，交射线 $C A$ 于点 $D$ ， $A C = 5$ ， $S_{△ A B C} = 10$ ，则 $t a n ∠ C B D$ 的值为．

查看试题解析
20. 如图， $▱ A B C D$ 中， $A E ⊥ B C$ ，垂足为点 $E$ ，点 $F$ 为 $C E$ 的中点，点 $G$ 为 $A B$ 的中点，分别连接 $B D$ 、 $F G$ ， $△ A B D$ 的面积为12， $B C = 8$ ，则线段 $F G$ 的长为．

查看试题解析

三、解答题

21. 先化简，再求值： $\frac{3 x - 6}{x^{2} + 4 x + 4} \div \frac{x - 2}{x + 2} - \frac{1}{x + 2}$ ，其中x＝2tan60°－4sin30°．

查看试题解析
22. 如图，在每个小正方形的边长均为1的方格纸中，有线段AB和线段CD，点A、B、C、D均在小正方形的顶点上．

(1)、在方格纸中画出以 $A B$ 为一边的 $△ A B E$ ，且 $△ A B E$ 的面积为3， $t a n ∠ A B E = \frac{1}{2}$ ，点 $E$ 在小正方形的顶点上；

(2)、在方格纸中画出以 $C D$ 为对角线的 $▱ F C G D$ ， $▱ F C G D$ 的周长为 $6 + 2 \sqrt{10}$ ，点 $F$ 、 $G$ 均在小正方形的顶点上，请你直接写出四边形 $F C G D$ 的面积．

查看试题解析
23. 某中学为评估九年级学生的学习状况，抽取了部分参加考试的学生的成绩进行样本分析，并绘制成了如下两幅不完整的统计图，请根据图中提供的信息解答下列问题：

(1)、求该中学抽取参加考试的学生的人数；

(2)、通过计算将条形统计图补充完整；

(3)、若该中学九年级共有450人参加了这次考试，请估计该中学九年级共有多少名学生的成绩达到成绩类别为优．

查看试题解析
24. 已知四边形 $A B C D$ 的对角线 $A C$ ， $B D$ 交于点 $O$ ， $A D ∥ B C$ ， $A B ∥ C D$ ，且 $A B = 5$ ， $A C = 8$ ， $B O = 3$ ．

(1)、如图1，求证：四边形 $A B C D$ 是菱形；

(2)、如图2，点 $F$ 为边 $C D$ 上一点，点 $E$ 为 $C B$ 延长线上一点，连接 $E F$ 交 $O B$ 于点 $G$ ，连接 $O F$ ， $O G = B G$ ， $E G = F G$ ，在不添加任何辅助线的情况下，请你直接写出图中长度为 $\frac{5}{2}$ 的四条线段．

查看试题解析
25. “六．一”儿童节将至，某玩具店准备购进甲、乙两种玩具，每个甲种玩具进价比每个乙种玩具进价少5元，已知用300元购进甲种玩具的数量等于用600元购进乙种玩具的数量．

(1)、求玩具店购进甲种玩具每个进价是多少元；

(2)、该玩具店准备用1000元全部用来购进甲、乙两种玩具，计划销售每个甲种玩具获得利润4元，销售每个乙种玩具获得利润5元，且销售两种玩具的总利润不低于600元，则该玩具店最多购进乙种玩具多少个？

查看试题解析
26. 已知 $A B$ 为 $⊙ O$ 的直径，弦 $C D$ 交 $A B$ 于点 $E$ ，弧 $B C =$ 弧 $B D$ ．

(1)、如图1，求证： $C E = D E$ ；

(2)、如图2，连接 $D O$ 并延长至点 $F$ ，连接 $E F$ 、 $B F$ ， $∠ B O F + 2 ∠ C E F = 180 °$ ，求证： $C D = 2 B F$ ；

(3)、如图3，在（2）的条件下，延长 $B F$ 交 $⊙ O$ 于点 $N$ ，连接 $D N$ 交 $E F$ 于点 $M$ ，点 $G$ 为 $D M$ 上一点，连接 $B G$ ， $B G = B N$ ，若 $D F = 2 D E$ ， $D G = 2$ ，求弦 $D N$ 的长．

查看试题解析
27. 在平面直角坐标系中，抛物线 $y = a x^{2} + b x + 4$ 与x轴交于点A、B，与y轴交于点C， $O B = O C$ ，连接AC， $t a n ∠ C A O = \frac{4}{3}$ ．

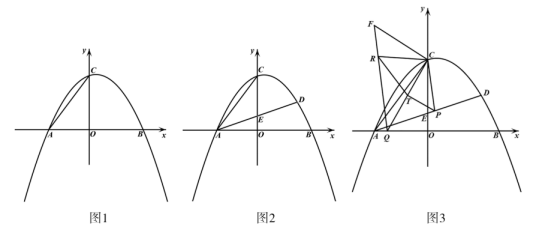(1)、如图1，分别求a、b的值；

(2)、如图2，点D为第一象限的抛物线上一点，连接AD交y轴于点E，设点D的横坐标为t， $△ A C E$ 的面积为s，求s与t的函数解析式（不要求写出自变量t的取值范围）；

(3)、如图3，在（2）的条件下，点D的横坐标是3，点Q在OA上，连接CQ，点T在CQ上，点R为第二象限内直线CQ左侧一点，连接RT、RC， $C R = T R$ ，连接QR并延长至点F，连接CF， $∠ C F R = ∠ C R T$ ， $C F = 2 F R$ ， $T P ⊥ C Q$ ，交AD于点P，若 $P C ： C Q = 5 ： 8$ ，求点P的坐标．

查看试题解析