黑龙江省哈尔滨市道外区2022年九年级中考二模考试数学试题

试卷更新日期：2022-05-30 类型：中考模拟

进入出卷网下载

一、单选题

1. 5的倒数是（）

A、 $\frac{1}{5}$ B、 $- 5$ C、 $- \frac{1}{5}$ D、 $5$

查看试题解析
2. 下列运算一定正确的是（）

A、 $a^{2} \cdot a = a^{3}$ B、 ${(a^{2})}^{3} = a^{5}$ C、 ${(a + 1)}^{2} = a^{2} + 1$ D、 $a^{3} + a = a^{3}$

查看试题解析
3. 下列图形中，既是轴对称图形又是中心对称图形的是（）．

A、 B、 C、 D、

查看试题解析
4. 七个大小相同的正方体搭成的几何体如图所示，其左视图是（）

A、 B、 C、 D、

查看试题解析
5. 反比例函数 $y = \frac{k}{x}$ 的图像经过点 $(- 1 ， 2)$ ，则k值为（）

A、2 B、-2 C、1 D、-1

查看试题解析
6. 方程 $\frac{3}{x + 2} = \frac{5}{x - 2}$ 的解为（）

A、 $x = 2$ B、 $x = 1$ C、 $x = 8$ D、 $x = - 8$

查看试题解析
7. 如图，一把梯子AB长4米，靠在垂直水平地面的墙上，若梯子与地面的夹角为 $α$ ，则梯子底端A到墙面的距离为（）

A、 $4 c o s α$ B、 $4 s i n α$ C、 $\frac{4}{c o s α}$ D、 $\frac{4}{s i n α}$

查看试题解析
8. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $∠ B A C = 30 °$ ，将 $△ A B C$ 绕点C按逆时针方向旋转 $α (0 ° < α < 90 °)$ 后得到 $△ D E C$ ，设CD交AB于点F，连接AD，若 $A F = A D$ ，则旋转角 $α$ 的度数为（）

A、50° B、40° C、30° D、20°

查看试题解析
9. 如图，在 $△ A B C$ 中， $D E ∥ B C$ ， $D F ∥ A C$ ， $A D = 2 B D$ ， $D E = 8$ ，则 $B F =$ （）．

A、2 B、3 C、4 D、5

查看试题解析
10. 抛物线 $y = a (x + 1) (x - k)$ 交x轴于点A、B（A左B右），交y轴于点C， $O B = O C$ ， $t a n ∠ C A O = 3$ ，则下列结论：①点A的坐标为 $(- 1 ， 0)$ ；② $a = - 1$ ；③B点坐标为 $(3 ， 0)$ ；④抛物线对称轴是直线 $x = 2$ ．其中正确的有（）．

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 中国国家统计局数据显示，2022年中国冰雪运动参与人数已达346000000，将“346000000”这个数字用科学记数法表示为．

查看试题解析
12. 函数 $y = \frac{3 x}{x - 3}$ 的自变量 $x$ 的取值范围是．

查看试题解析
13. 计算 $\sqrt{\frac{1}{2}} - \frac{1}{2} \sqrt{18}$ 的结果是．

查看试题解析
14. 分解因式： $m^{3} - 4 m n^{2} =$ ．

查看试题解析
15. 不等式组 ${\begin{array}{l} a - 2 < 2 a \\ 2 - a > 1 \end{array}$ 的解集是．

查看试题解析
16. 如图，在⊙O中，AB为直径，弦 $C D ⊥ A B$ 于点H，若 $A H = C D = 8$ ，则⊙O的半径长为．

查看试题解析
17. 一个扇形的圆心角为 $120 °$ ，面积为 $3 π c m^{2}$ ，则此扇形的半径是．

查看试题解析
18. 一个不诱明口袋里装有8个小球，其中黑球6个，白球2个，除颜色外均相同，从袋子中随机摸出一个小球，则摸出的小球是黑球的概率是．

查看试题解析
19. 在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $A C = 8$ ， $B C = 6$ ， D是AB中点，点F在射线AC上，连接DF，将 $△ A D F$ 沿DF翻折，点A对应点为点G，当 $D G ⊥ A C$ 时，线段AG的长为．

查看试题解析
20. 在 $△ A B C$ 中， $A B = A C$ ，点F在AC上，连接BF，延长CA至点D，连接BD，点H在线段BC上，连接DH交BF于点E，交AB于点G，若 $∠ B A C = ∠ B E H = 120 °$ ， $∠ A B F = ∠ A B D$ ， $C H = 3$ ，则 $A D =$ ．

查看试题解析

三、解答题

21. 先化简，再求代数式 $\frac{2}{x^{2} - 9} \div (1 - \frac{x + 2}{x + 3})$ 的值，其中x=2cos30^o+3tan45^o.

查看试题解析
22. 如图，网格中的每个小正方形的边长均为1，线段AB的端点均在小正方形的顶点上．
⑴在图中画出以AB为一边的菱形ABCD，点C和点D在小正方形顶点上；
⑵在图中画出以AB为斜边的直角三角形ABE，点E在小正方形顶点上，且 $t a n ∠ A B E = 2$ ，连接CE，请直接写出线段CE的长．

查看试题解析
23. 疫情期间，为了增强学生的自我保护意识，某校组织了一次全校2000名学生参加的“新冠疫情知多少”的考试，并随机抽查了部分参赛学生的成绩，根据成绩分成如下四个组： $A ： 60 \leq x < 70$ ， $B ： 70 \leq x < 80$ ， $C ： 80 \leq x < 90$ ， $D ： 90 \leq x < 100$ ，绘制成了两幅不完整的统计图，请你根据统计图上提供的信息回答下列问题：

(1)、这次被调查的学生共有多少人，并将条形统计图补充完整；

(2)、在扇形统计图中，求出m值；

(3)、请你估计该校学生得分80分及以上的学生人数．

查看试题解析
24. 如图， $D B ∥ A C$ ， $D B = \frac{1}{2} A C$ ， E是AC中点．

(1)、求证： $D E = B C$ ；

(2)、连接AD、BE，在不添加辅助线的情况下，请直接写出与 $△ A B D$ 面积相等的所有三角形．

查看试题解析
25. 兴发服装店老板用4500元购进一批某款T恤衫，由于深受顾客喜爱，很快售完，老板又用4950元购进第二批该款式T恤衫，所购数量与第一批相同，但每件进价比第一批多了9元．

(1)、第一批该款式T恤衫每件进价是多少元？

(2)、老板以每件120元的价格销售该款式T恤衫，当第二批T恤衫售出 $\frac{4}{5}$ 时，出现了滞销，于是决定降价促销，若要使第二批的销售利润不低于650元，剩余的T恤衫每件售价至少要多少元？（利润=售价﹣进价）

查看试题解析
26. 已知： $△ A B C$ 内接于⊙O，弦AF平分 $∠ B A C$ ，连接OF交BC于G．

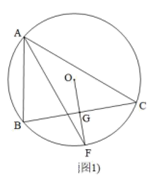
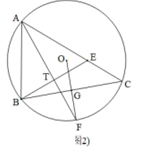
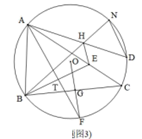(1)、如图1，求证： $O F ⊥ B C$ ；

(2)、如图2，过点B作 $B E ⊥ A F$ 于点T，BT延长线交AC于点E，若 $O G = F G$ ，求证： $△ A B E$ 为等边三角形；

(3)、如图3，在（2）的条件下，在⊙O上再取D、N两点，连接AD、BN交于点H，连接HE，若HE平分 $∠ B H D$ ， $A B = 5$ ， $D N = 3$ ，求⊙O的半径．

查看试题解析
27. 如图，在平面直角坐标系中，点O为坐标原点，直线 $y = x + 4$ 分别交x轴、y轴于点A、C，过点C的直线 $y = - x + b$ 交x轴正半轴于点B．

(1)、求点B坐标；

(2)、点P为线段BC上一点（不与点B、C重合），连接OP，过点O作 $O Q ⊥ O P$ 交AC于点Q，连接PQ，设点P横坐标为t， $△ P O Q$ 的面积为S，求S与t之间的函数解析式（不要求写出自变量的取值范围）；

(3)、在（2）的条件下，点D为y轴负半轴上一点，连接PA、PD、BD，若 $∠ A Q O - ∠ P A B = 3 ∠ P O B$ ， $∠ P D B = 2 ∠ P A B$ ，求直线BD的解析式．

查看试题解析