黑龙江省大庆市2022年九年级中考二模数学试题

试卷更新日期：2022-05-30 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列各数中，是负数的是（）

A、|﹣2| B、 ${(- \sqrt{5})}^{2}$ C、（-1）⁰ D、﹣3²

查看试题解析
2. 在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. “绿水青山就是金山银山”．某地积极响应党中央号召，大力推进农村厕所革命，已经累计投资 $1.012 \times 1 0^{8}$ 元资金．数据 $1.012 \times 1 0^{8}$ 可表示为（）

A、10.12亿 B、1.012亿 C、101.2亿 D、1012亿

查看试题解析
4. 如图，将数轴上-6与6两点间的线段六等分，这五个等分点所对应数依次为 $a_{1}$ ， $a_{2}$ ， $a_{3}$ ， $a_{4}$ ， $a_{5}$ ，则下列正确的是（）

A、 $a_{3} > 0$ B、 $| a_{1} | = | a_{4} |$ C、 $a_{1} + a_{2} + a_{3} + a_{4} + a_{5} = 0$ D、 $a_{2} + a_{5} < 0$

查看试题解析
5. 若 $a = \sqrt[3]{7}$ ， $b = \sqrt{5}$ ， $c = 2$ ，则a ， b ， c的大小关系为（）

A、 $b < c < a$ B、 $b < a < c$ C、 $a < c < b$ D、 $a < b < c$

查看试题解析
6. 正比例函数 $y = - k x$ 经过 $(1 ， - 6)$ ，则对于反比例函数 $y = \frac{k}{x}$ ，下列结论错误的是（）

A、图象经过第一、三象限 B、图象经过点 $(2 ， 3)$ C、当 $x > 1$ 时， $0 < y < 6$ D、函数值y随x的增大而减小

查看试题解析
7. 由一些大小相同的小正方体搭成的几何体的主视图和俯视图如图所示，则搭成该几何体的小正方体的个数最多为（）

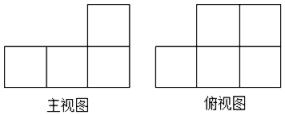A、7个 B、8个 C、9个 D、10个

查看试题解析
8. 如图，矩形ABCD的边CD上有一点E，∠DAE＝22.5°，EF⊥AB，垂足为F，将△AEF绕着点F顺时针旋转，使得点A的对应点M落在EF上，点E恰好落在点B处，连接BE．下列结论：①BM⊥AE；②四边形EFBC是正方形；③∠EBM＝30°；④ $S_{四边形 B C E M} ： S_{△ B F M} = (2 \sqrt{2} + 1) ： 1$ ．其中结论正确的序号是（）

A、①② B、①②③ C、①②④ D、③④

查看试题解析
9. 某学校初一年级学生来自农村，牧区，城镇三类地区，下面是根据其人数比例绘制的扇形统计图，由图中的信息，得出以下3个判断，错误的有（）
①该校初一学生在这三类不同地区的分布情况为3：2：7

②若已知该校来自牧区的初一学生为140人，则初一学生总人数为1080人．

③若从该校初一学生中抽取120人作为样本调查初一学生父母的文化程度，则从农村、牧区、城镇学生中分别随机抽取30、20、70人，样本更具有代表性．

A、3个 B、2个 C、1个 D、0个

查看试题解析
10. 如图，已知抛物线 $y = a x^{2} + b x + c$ 的对称轴在 $y$ 轴右侧，抛物线与 $x$ 轴交于点 $A (- 2 ， 0)$ 和点 $B$ ，与 $y$ 轴的负半轴交于点 $C$ ，且 $O B = 2 O C$ ，则下列结论：① $\frac{a - b}{c} > 0$ ；② $2 b - 4 a c = 1$ ；③ $a = \frac{1}{4}$ ；④当 $- 1 < b < 0$ 时，在 $x$ 轴下方的抛物线上一定存在关于对称轴对称的两点 $M$ ， $N$ （点 $M$ 在点 $N$ 左边），使得 $A N ⊥ B M$ .其中正确的有（）

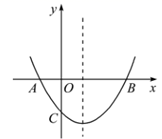A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 化简： $\sqrt{4}$ =

查看试题解析
12. 已知非零实数x，y满足 $y = \frac{x}{x + 1}$ ，则 $\frac{x - 2 x y - y}{x y} =$ ．

查看试题解析
13. 如果把一个圆柱体橡皮泥的一半捏成与圆柱底面积相等的圆锥，则这个圆锥的高与圆柱的高的比为．

查看试题解析
14. 古希腊数学家把1，3，6，10，15，21，…这样的数叫做三角形数，因为它的规律性可以用如图表示.根据图形，若把第一个图形表示的三角形数记为 $a_{1} = 1$ ，第二个图形表示的三角形数记为 $a_{2} = 3$ ，…，则第 $n$ 个图形表示的三角形数 $a_{n}$ ＝.（用含 $n$ 的式子表达）

查看试题解析
15. 若直角三角形其中两条边的长分别为3，4，则该直角三角形斜边上的高的长为．

查看试题解析
16. 如图，将边长为1的正方形 $A B C D$ 绕点 $A$ 顺时针旋转 $30 °$ 到 $A B_{1} C_{1} D_{1}$ 的位置，则阴影部分的面积是；

查看试题解析
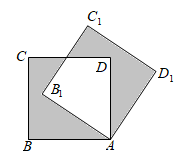17. 某快餐店销售A、B两种快餐，每份利润分别为12元、8元，每天卖出份数分别为40份、80份.该店为了增加利润，准备降低每份A种快餐的利润，同时提高每份B种快餐的利润.售卖时发现，在一定范围内，每份A种快餐利润每降1元可多卖2份，每份B种快餐利润每提高1元就少卖2份.如果这两种快餐每天销售总份数不变，那么这两种快餐一天的总利润最多是元.

查看试题解析

三、解答题

18. 如图是边长为2的等边三角形 $A B C$ ， D为 $△ A B C$ 内（包括 $△ A B C$ 的边）一动点，且满足 $C D^{2} = A D^{2} + B D^{2}$ ，则 $C D$ 的长度m的取值范围为．

查看试题解析
19. 计算： $202 2^{0} - 1^{- 1} + \sqrt{2} s i n 45 °$ ．

查看试题解析
20. 已知 $x + y = 4$ ， $x y = 3$ ，求 $x^{2} + y^{2}$ 的值．

查看试题解析
21. 解方程： $\frac{3 x}{x + 2} + \frac{2}{x - 2} = 3$ ．

查看试题解析
22. 某镇为创建特色小镇，助力乡村振兴，决定在辖区的一条河上修建一座步行观光桥，如图，该河旁有一座小山，山高 $B C = 80 m$ ，坡面 $A B$ 的坡度 $i = 1 ： 0.7$ （注：从山顶 $B$ 处测得河岸 $E$ 和对岸 $F$ 的俯角分别为 $∠ D B E = 45 °$ ， $∠ D B F = 31 °$ ．

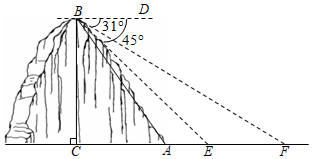(1)、求山脚 $A$ 到河岸 $E$ 的距离；

(2)、若在此处建桥，试求河宽 $E F$ 的长度．（结果精确到 $0.1 m$ ）
（参考数据： $s i n 31 ° ≈ 0.52$ ， $c o s 31 ° ≈ 0.86$ ， $t a n 31 ° \approx 0.60$ ）

查看试题解析
23. 高铁的开通，给衢州市民出行带来了极大的方便，“五一”期间，乐乐和颖颖相约到杭州市的某游乐园游玩，乐乐乘私家车从衢州出发1小时后，颖颖乘坐高铁从衢州出发，先到杭州火车站，然后再转车出租车取游乐园（换车时间忽略不计），两人恰好同时到达游乐园，他们离开衢州的距离y（千米）与乘车时间t（小时）的关系如图所示．
请结合图象解决下面问题：

(1)、高铁的平均速度是每小时多少千米？

(2)、当颖颖达到杭州火车东站时，乐乐距离游乐园还有多少千米？

(3)、若乐乐要提前18分钟到达游乐园，问私家车的速度必须达到多少千米/小时？

查看试题解析
24. 如图，在正方形 $A B C D$ 中， $A B = 6$ ， E为 $B C$ 中点，连接 $A E$ ，将 $△ A B E$ 沿 $A E$ 折叠，点B的对应点为G，连接 $E G$ 并延长交 $C D$ 于点F，连接 $A F$ ， $C G$ ．

(1)、判断 $C G$ 与 $A E$ 的位置关系，并说明理由；

(2)、求 $D F$ 的长．

查看试题解析

25. 疫苗接种初期，为更好地响应国家对符合条件的人群接种新冠疫苗的号召，某市教育部门随机抽取了该市部分七、八、九年级教师，了解教师的疫苗接种情况，得到如下统计表：

	已接种	未接种	合计
七年级	30	10	40
八年级	35	15	$a$
九年级	40	$b$	60
合计	105	$c$	150

(1)、表中，

a =

，

b =

，

c =

；

(2)、由表中数据可知，统计的教师中接种率最高的是年级教师；（填“七”或“八”或“九”）

(3)、若该市初中七、八、九年级一共约有8000名教师，根据抽样结果估计未接种的教师约有人；

(4)、为更好地响应号召，立德中学从最初接种的4名教师（其中七年级1名，八年级1名，九年级2名）中随机选取2名教师谈谈接种的感受，请用列表或画树状图的方法，求选中的两名教师恰好不在同一年级的概率.

查看试题解析

26. 如图，一次函数 $y = m x + 1$ 的图象与反比例函数 $y = \frac{k}{x}$ 的图象交于点A，B，交y轴于点C，点B的横坐标为1，且 $A C = 2 C B$ ，连接 $O A$ ， $O B$ ．

(1)、求 $△ A O B$ 的面积；

(2)、求反比例函数的表达式；

(3)、根据图象直接写出满足不等式 $\frac{k}{x} < m x + 1$ 时，x的取值范围．

查看试题解析
27. 如图，已知以 $B C$ 为斜边的 $R t △ A B C$ 内接于 $☉ O$ ， $∠ B A C$ 的平分线交 $☉ O$ 于点D，过点D作 $D E ∥ B C$ 交 $A B$ 的延长线于点E，连接 $D B$ ， $D C$ ．

(1)、求证： $E D$ 为 $☉ O$ 的切线；

(2)、求证： $B C^{2} = 2 E D \cdot F C$ ；

(3)、若 $t a n ∠ A B C = 2$ ， $A D = \frac{3 \sqrt{2}}{2}$ ，求 $B C$ 的长．

查看试题解析
28. 如图，抛物线 $y = m x^{2} + (m^{2} + 3) x - (6 m + 9)$ 与x轴交于点A，B，与y轴交于点C，已知点 $B (3 ， 0)$ ．

(1)、求直线 $B C$ 及抛物线的函数表达式；

(2)、P为x轴上方抛物线上一点．
①若 $S_{△ P B C} = S_{△ A B C}$ ，请直接写出点P的坐标；
②如图， $P D ∥ y$ 轴交 $B C$ 于点D， $D E ∥ x$ 轴交 $A C$ 于点E，求 $P D + D E$ 的最大值；

(3)、Q为抛物线上一点，若 $∠ A C Q = 45 °$ ，求点Q的坐标．

查看试题解析