河北省唐山市滦州市2022年中考一模数学试题
试卷更新日期:2022-05-30 类型:中考模拟
一、单选题
-
1. 在小河旁有一村庄,现要建一取水点,为使该村村民到河边取水最近,则取水点应建在( )
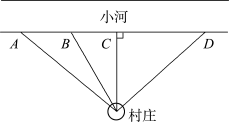 A、A点 B、B点 C、C点 D、D点2. 成人每天维生素D的摄入量约为0.0000046克.数据“0.0000046”用科学记数法表示为( )A、 B、 C、 D、3. 如图所示的几何体的左视图是( )
A、A点 B、B点 C、C点 D、D点2. 成人每天维生素D的摄入量约为0.0000046克.数据“0.0000046”用科学记数法表示为( )A、 B、 C、 D、3. 如图所示的几何体的左视图是( )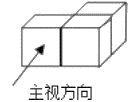 A、
A、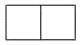 B、
B、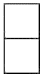 C、
C、 D、
D、 4. 实数 的值在( )A、5和6之间 B、6和7之间 C、7和8之间 D、8和9之间5. 对于① ,② ,从左到右的变形,表述正确的是( )A、都是因式分解 B、都是乘法运算 C、①是因式分解,②是乘法运算 D、①是乘法运算,②是因式分解6. 不等式3(1﹣x)>2﹣4x的解在数轴上表示正确的是( )A、
4. 实数 的值在( )A、5和6之间 B、6和7之间 C、7和8之间 D、8和9之间5. 对于① ,② ,从左到右的变形,表述正确的是( )A、都是因式分解 B、都是乘法运算 C、①是因式分解,②是乘法运算 D、①是乘法运算,②是因式分解6. 不等式3(1﹣x)>2﹣4x的解在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 7. 如图,在 中, ,则 的中线 的长为( )
7. 如图,在 中, ,则 的中线 的长为( ) A、5 B、6 C、8 D、108. 已知一元二次方程的常数项被墨水污染,当此方程有实数根时,污染的常数项可以是( )
A、5 B、6 C、8 D、108. 已知一元二次方程的常数项被墨水污染,当此方程有实数根时,污染的常数项可以是( ) A、3 B、2 C、1 D、09. 下列说法正确的是( )A、检测某批次灯泡的使用寿命,适宜用全面调查 B、“367人中有2人同月同日生”为必然事件 C、可能性是1%的事件在一次试验中一定不会发生 D、的相反数是-310. 已知▱ABCD,根据图中尺规作图的痕迹,判断下列结论中不一定成立的是( )
A、3 B、2 C、1 D、09. 下列说法正确的是( )A、检测某批次灯泡的使用寿命,适宜用全面调查 B、“367人中有2人同月同日生”为必然事件 C、可能性是1%的事件在一次试验中一定不会发生 D、的相反数是-310. 已知▱ABCD,根据图中尺规作图的痕迹,判断下列结论中不一定成立的是( ) A、∠DAE=∠BAE B、∠DEA= ∠DAB C、DE=BE D、BC=DE11. 如图,把△ABC先向右平移3个单位,再向上平移2个单位得到△DEF,则顶点C(0,-1)对应点的坐标为( )
A、∠DAE=∠BAE B、∠DEA= ∠DAB C、DE=BE D、BC=DE11. 如图,把△ABC先向右平移3个单位,再向上平移2个单位得到△DEF,则顶点C(0,-1)对应点的坐标为( )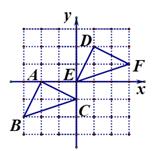 A、(0,0) B、(1,2) C、(1,3) D、(3,1)12. 如图,一块直角三角板的角的顶点落在上,两边分别交于、两点,若的直径为8,则弦长为( )
A、(0,0) B、(1,2) C、(1,3) D、(3,1)12. 如图,一块直角三角板的角的顶点落在上,两边分别交于、两点,若的直径为8,则弦长为( ) A、8 B、4 C、 D、13. 某工厂计划生产1500个零件,但是在实际生产时,……,求实际每天生产零件的个数,在这个题目中,若设实际每天生产零件x个,可得方程 ,则题目中用“……”表示的条件应是( )
A、8 B、4 C、 D、13. 某工厂计划生产1500个零件,但是在实际生产时,……,求实际每天生产零件的个数,在这个题目中,若设实际每天生产零件x个,可得方程 ,则题目中用“……”表示的条件应是( )
A、每天比原计划多生产5个,结果延期10天完成 B、每天比原计划多生产5个,结果提前10天完成 C、每天比原计划少生产5个,结果延期10天完成 D、每天比原计划少生产5个,结果提前10天完成14. 已知点(﹣2,a),(2,b),(3,c)在函数y= (k>0)的图象上,则下列判断正确的是( )A、a<b<c B、b<a<c C、a<c<b D、c<b<a15. 如图,在中,是延长线上一点,分别与交于点 . 下列结论:①;②;③;④ , 其中正确的个数是( ) A、1 B、2 C、3 D、416. 如图,菱形ABCD的边长为2,∠A=60°,点P和点Q分别从点B和点C出发,沿射线BC向右运动,且速度相同,过点Q作QH⊥BD,垂足为H,连接PH,设点P运动的距离为x(0<x≤2),△BPH的面积为S,则能反映S与x之间的函数关系的图象大致为( )
A、1 B、2 C、3 D、416. 如图,菱形ABCD的边长为2,∠A=60°,点P和点Q分别从点B和点C出发,沿射线BC向右运动,且速度相同,过点Q作QH⊥BD,垂足为H,连接PH,设点P运动的距离为x(0<x≤2),△BPH的面积为S,则能反映S与x之间的函数关系的图象大致为( ) A、
A、 B、
B、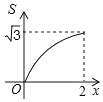 C、
C、 D、
D、
二、填空题
-
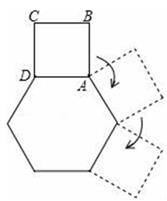
17. 式子在实数范围内有意义,则实数x的取值范围是 .18. 若(x+1)(x+a)=x2+bx-3,则ab的值为 .19. 如图,边长为1的正方形ABCD在等边长的正六边形外部做顺时针滚动,滚动一周回到初始位置时停止.第一次滚动时正方形旋转了°,点A在滚动过程中到出发点的最大距离是 .
三、解答题
-
20. 计算: .21. 观察下列两个等式: , ,给出定义如下:我们称使等式 成立的一对有理数“ , ”为“共生有理数对”,记为 ,如:数对 , 都是“共生有理数对”.(1)、通过计算判断数对“1,2”是不是“共生有理数对”;(2)、若 是“共生有理数对”,求a的值;(3)、若 是“共生有理数对”,则“ , ”“共生有理数对”(填“是”或“不是”);(4)、如果 是“共生有理数对”(其中 ),直接用含n的式子表示m.22. 3月6日开学啦!为了解学生的体温情况,班主任张老师根据全班学生某天上午的《体温监测记载表》,绘制了如下不完整的频数分布表和扇形统计图.
学生体温频数分布表
组别
温度(℃)
频数(人数)
甲
36.3
8
乙
36.4
a
丙
36.5
24
丁
36.6
4
请根据以上信息,解答下列问题:
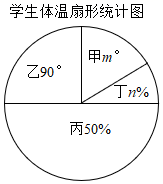 (1)、频数分布表中a= , 该班学生体温的众数是℃,中位数是℃;(2)、扇形统计图中甲所对应圆心角度数m°为=度,丁组对应的扇形的圆心角是度;(3)、体温测量为36.6℃的4位同学中,男女生各两名,班主任准备从这四名同学中选出两名同学参加学校的新冠肺炎疫情防控知识宣传小组,请你用列表法或画树状图的方法求出所选两名同学正好都是女生的概率.23. 一辆汽车行驶时的耗油量为0.1升/千米,如图是油箱剩余油量 (升)关于加满油后已行驶的路程 (千米)的函数图象.
(1)、频数分布表中a= , 该班学生体温的众数是℃,中位数是℃;(2)、扇形统计图中甲所对应圆心角度数m°为=度,丁组对应的扇形的圆心角是度;(3)、体温测量为36.6℃的4位同学中,男女生各两名,班主任准备从这四名同学中选出两名同学参加学校的新冠肺炎疫情防控知识宣传小组,请你用列表法或画树状图的方法求出所选两名同学正好都是女生的概率.23. 一辆汽车行驶时的耗油量为0.1升/千米,如图是油箱剩余油量 (升)关于加满油后已行驶的路程 (千米)的函数图象.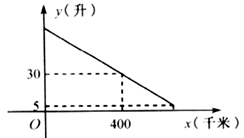 (1)、根据图象,直接写出汽车行驶400千米时,油箱内的剩余油量,并计算加满油时油箱的油量;(2)、求 关于 的函数关系式,并计算该汽车在剩余油量5升时,已行驶的路程.24. 如图,射线AM⊥AB,O是AM上的一点,以O为圆心,OA长为半径,在AM上方作半圆AOC,BE与半圆相切于点D,交AM于点E,EF⊥BO于点F.
(1)、根据图象,直接写出汽车行驶400千米时,油箱内的剩余油量,并计算加满油时油箱的油量;(2)、求 关于 的函数关系式,并计算该汽车在剩余油量5升时,已行驶的路程.24. 如图,射线AM⊥AB,O是AM上的一点,以O为圆心,OA长为半径,在AM上方作半圆AOC,BE与半圆相切于点D,交AM于点E,EF⊥BO于点F.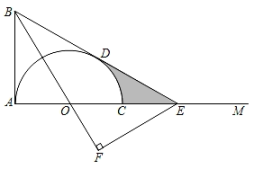 (1)、求证:BA=BD;(2)、若∠ABE=60°,
(1)、求证:BA=BD;(2)、若∠ABE=60°,①判断点F与半圆AOC所在圆的位置关系,并说明理由;
②若AB= , 直接写出阴影部分的面积.
25. 如图,在平面直角坐标系中,已知二次函数 图象的顶点为A,与y轴交于点B,异于顶点A的点C(1,n)在该函数图象上. (1)、当m=5时,求n的值.(2)、当n=2时,若点A在第一象限内,结合图象,求当y 时,自变量x的取值范围.(3)、作直线AC与y轴相交于点D.当点B在x轴上方,且在线段OD上时,求m的取值范围.26. 如图1,图2中,正方形ABCD的边长为6,点P从点B出发沿边BC—CD以每秒2个单位长的速度向点D匀速运动,以BP为边作等边三角形BPQ,使点Q在正方形ABCD内或边上,当点Q恰好运动到AD边上时,点P停止运动。设运动时间为t秒(t≥0)。
(1)、当m=5时,求n的值.(2)、当n=2时,若点A在第一象限内,结合图象,求当y 时,自变量x的取值范围.(3)、作直线AC与y轴相交于点D.当点B在x轴上方,且在线段OD上时,求m的取值范围.26. 如图1,图2中,正方形ABCD的边长为6,点P从点B出发沿边BC—CD以每秒2个单位长的速度向点D匀速运动,以BP为边作等边三角形BPQ,使点Q在正方形ABCD内或边上,当点Q恰好运动到AD边上时,点P停止运动。设运动时间为t秒(t≥0)。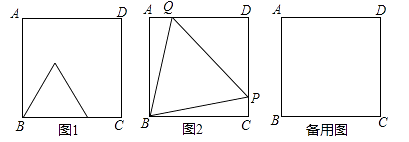 (1)、当t=2时,点Q到BC的距离=;(2)、当点P在BC边上运动时,求CQ的最小值及此时t的值;(3)、若点Q在AD边上时,如图2,求出t的值;(4)、直接写出点Q运动路线的长。
(1)、当t=2时,点Q到BC的距离=;(2)、当点P在BC边上运动时,求CQ的最小值及此时t的值;(3)、若点Q在AD边上时,如图2,求出t的值;(4)、直接写出点Q运动路线的长。