河北省唐山市曹妃甸区2022年中考一模数学试题
试卷更新日期:2022-05-30 类型:中考模拟
一、单选题
-
1. 如图,与互为内错角的( )
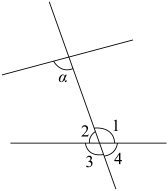 A、 B、 C、 D、2. 已知 ,下列式子不一定成立的是( )A、 B、 C、 D、3. 在解二元一次方程组时,若①-②可直接消去未知数y,则和( )A、互为倒数 B、大小相等 C、都等于0 D、互为相反数4. 若55+55+55+55+55=25n , 则n的值为( )A、10 B、6 C、5 D、35. 数轴上A,B,C,D四点中,两点之间的距离最接近于的是( )
A、 B、 C、 D、2. 已知 ,下列式子不一定成立的是( )A、 B、 C、 D、3. 在解二元一次方程组时,若①-②可直接消去未知数y,则和( )A、互为倒数 B、大小相等 C、都等于0 D、互为相反数4. 若55+55+55+55+55=25n , 则n的值为( )A、10 B、6 C、5 D、35. 数轴上A,B,C,D四点中,两点之间的距离最接近于的是( ) A、点A和点B B、点B和点C C、点C和点D D、点A和点C6. 一组数据3,5,5,7,若添加一个数据5,则发生变化的统计量是( )A、平均数 B、中位数 C、方差 D、众数7. 围棋起源于中国,古代称之为“弈”,至今已有四千多年的历史.下列由黑白棋子摆成的图案是中心对称图形的是( )A、
A、点A和点B B、点B和点C C、点C和点D D、点A和点C6. 一组数据3,5,5,7,若添加一个数据5,则发生变化的统计量是( )A、平均数 B、中位数 C、方差 D、众数7. 围棋起源于中国,古代称之为“弈”,至今已有四千多年的历史.下列由黑白棋子摆成的图案是中心对称图形的是( )A、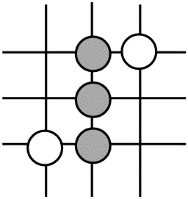
B、
B、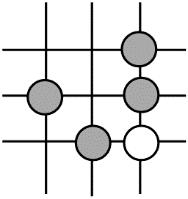
C、
C、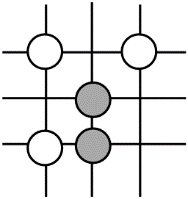
D、
D、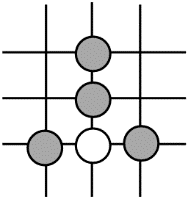
8. 如图是由若干个完全相同的小正方体组合而成的几何体,若将小正方体①移动到小正方体②的正上方,下列关于移动后几何体的三视图说法正确的是( )
8. 如图是由若干个完全相同的小正方体组合而成的几何体,若将小正方体①移动到小正方体②的正上方,下列关于移动后几何体的三视图说法正确的是( ) A、左视图发生变化 B、俯视图发生变化 C、主视图发生改变 D、三个视图都发生改变9. 如图,在处测得点在北偏东方向上,在处测得点在北偏东方向上,若千米,则点两点的距离为( )千米.
A、左视图发生变化 B、俯视图发生变化 C、主视图发生改变 D、三个视图都发生改变9. 如图,在处测得点在北偏东方向上,在处测得点在北偏东方向上,若千米,则点两点的距离为( )千米. A、4 B、 C、2 D、610. 如图,点是正六边形内部一个动点, , 则点到这个正六边形六条边的距离之和为( ) .
A、4 B、 C、2 D、610. 如图,点是正六边形内部一个动点, , 则点到这个正六边形六条边的距离之和为( ) . A、6 B、3 C、 D、11. 亮亮在解一元二次方程: □ 时,不小心把常数项丢掉了,已知这个一元二次方程有实数根,则丢掉的常数项的最大值是( )A、1 B、0 C、7 D、912. 如图,RtΔABC中,AB=9,BC=6,∠B=90°,将ΔABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为( )
A、6 B、3 C、 D、11. 亮亮在解一元二次方程: □ 时,不小心把常数项丢掉了,已知这个一元二次方程有实数根,则丢掉的常数项的最大值是( )A、1 B、0 C、7 D、912. 如图,RtΔABC中,AB=9,BC=6,∠B=90°,将ΔABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为( ) A、 B、 C、4 D、513. 已知,在中, , 求作的外心O,以下是甲、乙两同学的作法:
A、 B、 C、4 D、513. 已知,在中, , 求作的外心O,以下是甲、乙两同学的作法:

对于两人的作法,正确的是( )
A、两人都对 B、两人都不对 C、甲对,乙不对 D、甲不对,乙对14. “今有井径五尺,不知其深,立五尺木于井上,从末望水岸,入径四寸,问井深几何?”这是我国古代数学著作《九章算术》中的“井深几何”问题,它的题意可以由示意图获得.设井深为 尺,所列方程正确的是( )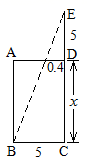 A、 B、 C、 D、15. 如图,直线 和 与x轴分别相交于点 ,点 ,则 解集为( )
A、 B、 C、 D、15. 如图,直线 和 与x轴分别相交于点 ,点 ,则 解集为( )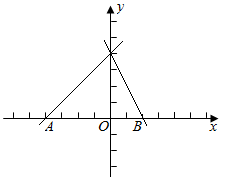 A、 B、 C、 D、 或16. 如图,在中, , , , 点O是AB的三等分点,半圆O与AC相切,M,N分别是BC与半圆弧上的动点,则MN的最小值和最大值之和是( )
A、 B、 C、 D、 或16. 如图,在中, , , , 点O是AB的三等分点,半圆O与AC相切,M,N分别是BC与半圆弧上的动点,则MN的最小值和最大值之和是( )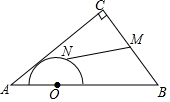 A、5 B、6 C、7 D、8
A、5 B、6 C、7 D、8二、填空题
-
17. 如图,在Rt△ABC中,∠C=90°,直线DE是边AB的垂直平分线,连接BE.
 (1)、若∠A=35°,则∠CBE=;(2)、若AE=3,EC=1,则△ABC的面积为 .18. 某矩形人行道由相同的灰色正方形地砖与相同的白色等腰直角三角形地砖排列而成,图1表示此人行道的地砖排列方式,其中正方形地砖为连续排列.
(1)、若∠A=35°,则∠CBE=;(2)、若AE=3,EC=1,则△ABC的面积为 .18. 某矩形人行道由相同的灰色正方形地砖与相同的白色等腰直角三角形地砖排列而成,图1表示此人行道的地砖排列方式,其中正方形地砖为连续排列.
当正方形地砖只有1块时,等腰直角三角形地砖有6块(如图2);当正方形地砖有2块时,等腰直角三角形地砖有8块(如图3),以此类推.
(1)、若人行道上每增加1块正方形地砖,则等腰直角三角形地砖增加块;(2)、现有2021块等腰直角三角形地砖,若按此规律再建一条人行道,要求等腰直角三角形地砖剩余最少,则需要正方形地砖块.19. 如图,在平面直角坐标系中,已知点A(1,1),点B(4,1),点C(2,3), (1)、若反比例函数y=的图象过点B,则k=;(2)、若反比例函数y=的图象与△ABC有公共点,则k的取值范围是 .
(1)、若反比例函数y=的图象过点B,则k=;(2)、若反比例函数y=的图象与△ABC有公共点,则k的取值范围是 .三、解答题
-
20. 洪洪同学在电脑中设置了一个有理数的运算程序:输入数“a”加“★”键再输入“b”,就可以得到运算 .(1)、按此程序;(2)、若淇淇输入数“-1”加“★”键再输入“x”后,电脑输出的数为1,求x的值;(3)、嘉嘉同学运用淇淇设置的在这个程序时,屏幕显示:“该操作无法进行,”你能说出嘉嘉在什么地方出错了吗?21. 某班开展了环保知识竞赛,学习委员为班级购买奖品后与班长对话如下:
 (1)、请用方程的知识帮助学习委员计算一下,为什么学习委员搞错了;(2)、学习委员拿出发票后,发现的确错了,因为他还买了一个笔记本,但笔记本的单价己模糊不清,只能认出单价是小于10的整数,那么笔记本的单价可能是多少元?22. 某市派遣由5名医护人员组成的一支医疗支援队支援邻市,已知这五名医护人员的年龄(单位:岁)分别是24,28,35,35,47,其中年龄为24岁和47岁的是女队员,其余是男队员.(1)、直接写出这5名医护人员年龄的众数和中位数;(2)、因工作需要,需增加1名医护人员,若增加后年龄的中位数小于原来年龄的中位数,则增加的医护人员的最大年龄是多少?(年龄为整数)(3)、若需要从男队员中选两名支援急救工作,用列表法求所选两名队员的年龄恰好相等的概率.23. 如图,点A、B分别在∠DPE两边上,且PA=PB,以AB为直径作半圆O,点C是半圆O的中点.
(1)、请用方程的知识帮助学习委员计算一下,为什么学习委员搞错了;(2)、学习委员拿出发票后,发现的确错了,因为他还买了一个笔记本,但笔记本的单价己模糊不清,只能认出单价是小于10的整数,那么笔记本的单价可能是多少元?22. 某市派遣由5名医护人员组成的一支医疗支援队支援邻市,已知这五名医护人员的年龄(单位:岁)分别是24,28,35,35,47,其中年龄为24岁和47岁的是女队员,其余是男队员.(1)、直接写出这5名医护人员年龄的众数和中位数;(2)、因工作需要,需增加1名医护人员,若增加后年龄的中位数小于原来年龄的中位数,则增加的医护人员的最大年龄是多少?(年龄为整数)(3)、若需要从男队员中选两名支援急救工作,用列表法求所选两名队员的年龄恰好相等的概率.23. 如图,点A、B分别在∠DPE两边上,且PA=PB,以AB为直径作半圆O,点C是半圆O的中点. (1)、连接AC、BC,求证:△PAC≌△PBC;(2)、若∠APB=60°,PA=4,通过计算比较PO与劣弧哪个更长;(3)、若点O是△PAB的外心,请直接写出四边形APBC的形状.24. I号无人机从海拔10m处出发,以10m/min的速度匀速上升,II号无人机从海拔30m处同时出发,以a(m/min)的速度匀速上升,经过5min两架无人机位于同一海拔高度b(m).无人机海拔高度y(m)与时间x(min)的关系如图.两架无人机都上升了15min.
(1)、连接AC、BC,求证:△PAC≌△PBC;(2)、若∠APB=60°,PA=4,通过计算比较PO与劣弧哪个更长;(3)、若点O是△PAB的外心,请直接写出四边形APBC的形状.24. I号无人机从海拔10m处出发,以10m/min的速度匀速上升,II号无人机从海拔30m处同时出发,以a(m/min)的速度匀速上升,经过5min两架无人机位于同一海拔高度b(m).无人机海拔高度y(m)与时间x(min)的关系如图.两架无人机都上升了15min.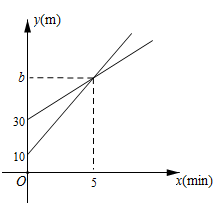 (1)、求b的值及II号无人机海拔高度y(m)与时间x(min)的关系式.(2)、问无人机上升了多少时间,I号无人机比II号无人机高28米.25. 已知抛物线(1)、当 时,请判断点(2,4)是否在该抛物线上;(2)、该抛物线的顶点随着m的变化而移动,当顶点移动到最高处时,求该抛物线的顶点坐标;(3)、已知点 、 ,若该抛物线与线段EF只有一个交点,求该抛物线顶点横坐标的取值范围.26. 已知:如图,在矩形ABCD中,AB=6cm,BC=8cm,对角线AC,BD交于点O.点P从点A出发,沿AD方向匀速运动,速度为1cm/s;同时,点Q从点D出发,沿DC方向匀速运动,速度为1cm/s;当一个点停止运动时,另一个点也停止运动,连接PO并延长,交BC于点E,过点Q作QF∥AC,交BD于点F.设运动时间为t(s)(0<t<6),解答下列问题:
(1)、求b的值及II号无人机海拔高度y(m)与时间x(min)的关系式.(2)、问无人机上升了多少时间,I号无人机比II号无人机高28米.25. 已知抛物线(1)、当 时,请判断点(2,4)是否在该抛物线上;(2)、该抛物线的顶点随着m的变化而移动,当顶点移动到最高处时,求该抛物线的顶点坐标;(3)、已知点 、 ,若该抛物线与线段EF只有一个交点,求该抛物线顶点横坐标的取值范围.26. 已知:如图,在矩形ABCD中,AB=6cm,BC=8cm,对角线AC,BD交于点O.点P从点A出发,沿AD方向匀速运动,速度为1cm/s;同时,点Q从点D出发,沿DC方向匀速运动,速度为1cm/s;当一个点停止运动时,另一个点也停止运动,连接PO并延长,交BC于点E,过点Q作QF∥AC,交BD于点F.设运动时间为t(s)(0<t<6),解答下列问题: (1)、当t为何值时,AP=PO;(2)、设五边形OECQF的面积为S(cm2),试确定S与t的函数关系式;(3)、在运动过程中,是否存在某一时刻t,使S五边形OECQF:S△ACD=9:16?若存在,求出t的值;若不存在,请说明理由;(4)、在运动过程中,是否存在某一时刻t,使OD平分∠COP?若存在,求出t的值;若不存在,请说明理由.
(1)、当t为何值时,AP=PO;(2)、设五边形OECQF的面积为S(cm2),试确定S与t的函数关系式;(3)、在运动过程中,是否存在某一时刻t,使S五边形OECQF:S△ACD=9:16?若存在,求出t的值;若不存在,请说明理由;(4)、在运动过程中,是否存在某一时刻t,使OD平分∠COP?若存在,求出t的值;若不存在,请说明理由.