广东省汕头市澄海区2022年初中学业水平模拟考试数学试题
试卷更新日期:2022-05-30 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、2022 B、-2022 C、1 D、-12. 我国自主研发的“北斗系统”现已广泛应用于国防、生产和生活等各个领域,多项技术处于国际领先地位,其星载原子钟的精度,已经提升到了每3000000年误差1秒.数3000000用科学记数法表示为( )A、 B、 C、 D、3. 一个不透明的袋子中装有3个白球,2个黑球,它们除了颜色外都相同.将球摇匀后,从中随机摸出一个球,记下颜色后放回,再随机摸出一个球.两次摸到的球颜色相同的概率是( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 若关于的一元二次方程有两个不相等的实数根,则的值可以是( )A、0 B、1 C、2 D、-26. 如图,在平面直角坐标系中,菱形的顶点 , , 在坐标轴上,若点、的坐标分别为、 , 则点的坐标为( )
 A、 B、 C、 D、7. 如图,为钝角三角形,将绕点A按逆时针方向旋转得到 , 连接 , 若 , 则的度数为
A、 B、 C、 D、7. 如图,为钝角三角形,将绕点A按逆时针方向旋转得到 , 连接 , 若 , 则的度数为 A、 B、 C、 D、8. 文具店销售某种书袋,每个12元,王老师计划去购买这种书袋若干个.结账时店员说:“如果你再多买一个就可以打九折,总价钱会便宜24元”.王老师说:“那就多买一个吧,谢谢!”根据两人的对话可求得王老师原计划要购买书袋( )个A、28 B、29 C、30 D、319. 如图,已知是的直径,半径 , 点在劣弧上(不与点、重合),与交于点 . 设 , , 则下列结论正确的是( )
A、 B、 C、 D、8. 文具店销售某种书袋,每个12元,王老师计划去购买这种书袋若干个.结账时店员说:“如果你再多买一个就可以打九折,总价钱会便宜24元”.王老师说:“那就多买一个吧,谢谢!”根据两人的对话可求得王老师原计划要购买书袋( )个A、28 B、29 C、30 D、319. 如图,已知是的直径,半径 , 点在劣弧上(不与点、重合),与交于点 . 设 , , 则下列结论正确的是( ) A、 B、 C、 D、10. 已知二次函数的图象如图所示,下列结论:①;②关于的不等式的解集为;③;④ . 其中正确结论的个数为( )
A、 B、 C、 D、10. 已知二次函数的图象如图所示,下列结论:①;②关于的不等式的解集为;③;④ . 其中正确结论的个数为( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
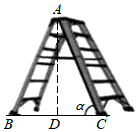
11. 分解因式:25﹣x2=.12. 若 , 则 .13. 计算 .14. 人字梯为现代家庭常用的工具.如图,若 , 的长都为 , 当时,人字梯顶端离地面的高度为 . (参考数据: , , )
 15. 如图,点在反比例函数的图象上,点在反比例函数的图象上,若轴,则的面积为 .
15. 如图,点在反比例函数的图象上,点在反比例函数的图象上,若轴,则的面积为 . 16. 如图所示,由8个有公共顶点O的等腰直角三角形拼成的图形,∠AOB=∠BOC=⋅⋅⋅=∠MON=45°.若OA=64,则ON的长为 .
16. 如图所示,由8个有公共顶点O的等腰直角三角形拼成的图形,∠AOB=∠BOC=⋅⋅⋅=∠MON=45°.若OA=64,则ON的长为 . 17. 如图,在中, , 点在边上.将沿直线翻折,点落在点处,连接 , 交于点 . 若 , , 则的值为 .
17. 如图,在中, , 点在边上.将沿直线翻折,点落在点处,连接 , 交于点 . 若 , , 则的值为 .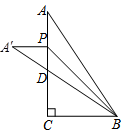
三、解答题
-
18. 计算: .19. 解不等式组: .20. 人们对网购的热衷促进了快递行业的发展,某快递站点为提高投递效率,给快递员配备了电动车,结果平均每人每天比原来多投递60件.若快递站点的快递员人数不变,站点投递快件的能力由每天400件提高到640件.求现在平均每人每天投递快件多少件?21. 如图,在中, , 是的中点,点在的延长线上.
 (1)、作的平分线 , 连接 , 并延长交于点 , 连接(用尺规作图,并在图中标明相应的字母,保留作图痕迹);(2)、在(1)的条件下,判断四边形的形状,并证明你的结论.22. 我市某学校为落实“立德树人”根本任务,构建“五育并举”课程体系,开设了“烹饪、园艺、电工、木工、缝纫”五大类劳动课程.为了解七年级学生对每类课程的选择情况,随机抽取了七年级若干名学生进行调查(每人只选一类最喜欢的课程),将调查结果绘制成如图两幅不完整的统计图:
(1)、作的平分线 , 连接 , 并延长交于点 , 连接(用尺规作图,并在图中标明相应的字母,保留作图痕迹);(2)、在(1)的条件下,判断四边形的形状,并证明你的结论.22. 我市某学校为落实“立德树人”根本任务,构建“五育并举”课程体系,开设了“烹饪、园艺、电工、木工、缝纫”五大类劳动课程.为了解七年级学生对每类课程的选择情况,随机抽取了七年级若干名学生进行调查(每人只选一类最喜欢的课程),将调查结果绘制成如图两幅不完整的统计图:劳动课程
烹饪
园艺
电工
木工
缝纫
人数
10
12
a
9
15
 (1)、 , , 扇形统计图中“烹饪”所对应扇形的圆心角;(2)、若该校七年级共有600名学生,请估计该校七年级学生选择“园艺”劳动课程的人数;(3)、七(1)班计划在“烹饪、园艺、电工、缝纫”四大类劳动课程中任选两类参加学校展示活动,请用列表或画树状图的方法,求恰好选中“园艺、缝纫”这两类劳动课程的概率.23. 如图,直线与相离,过点作于点 , 交于点 , 延长交于点 . 点、在直线上,连接并延长交于点 , 连接 , .
(1)、 , , 扇形统计图中“烹饪”所对应扇形的圆心角;(2)、若该校七年级共有600名学生,请估计该校七年级学生选择“园艺”劳动课程的人数;(3)、七(1)班计划在“烹饪、园艺、电工、缝纫”四大类劳动课程中任选两类参加学校展示活动,请用列表或画树状图的方法,求恰好选中“园艺、缝纫”这两类劳动课程的概率.23. 如图,直线与相离,过点作于点 , 交于点 , 延长交于点 . 点、在直线上,连接并延长交于点 , 连接 , . (1)、求证:是的切线;(2)、若 , , , 求的半径和弦的长.24. 如图,已知矩形中, , , 点 , 分别在边 , 上,沿着折叠矩形 , 使点 , 分别落在 , 处,且点在线段上(不与两端点重合),过点作于点 , 连接 .
(1)、求证:是的切线;(2)、若 , , , 求的半径和弦的长.24. 如图,已知矩形中, , , 点 , 分别在边 , 上,沿着折叠矩形 , 使点 , 分别落在 , 处,且点在线段上(不与两端点重合),过点作于点 , 连接 .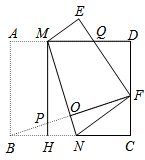 (1)、求证:;(2)、若 , 求的长;(3)、若 , 求折叠后重叠部分的面积.25. 如图,抛物线交轴于、两点,交轴于点 , 点的坐标为 , 点坐标为 , 对称轴为 . 点为线段上的一个动点(不与两端点重合),过点作轴,交抛物线于点 , 交于点 .
(1)、求证:;(2)、若 , 求的长;(3)、若 , 求折叠后重叠部分的面积.25. 如图,抛物线交轴于、两点,交轴于点 , 点的坐标为 , 点坐标为 , 对称轴为 . 点为线段上的一个动点(不与两端点重合),过点作轴,交抛物线于点 , 交于点 . (1)、求抛物线及直线的表达式;(2)、过点作 , 垂足为点 . 求线段的最大值;(3)、试探究点在运动过程中,是否存在这样的点 , 使得以 , , 为顶点的三角形是等腰三角形.若存在,请求出此时点的坐标;若不存在,请说明理由.
(1)、求抛物线及直线的表达式;(2)、过点作 , 垂足为点 . 求线段的最大值;(3)、试探究点在运动过程中,是否存在这样的点 , 使得以 , , 为顶点的三角形是等腰三角形.若存在,请求出此时点的坐标;若不存在,请说明理由.