广东省汕头市潮南区2022年中考模拟考试数学试题
试卷更新日期:2022-05-30 类型:中考模拟
一、单选题
-
1. 在实数0,-π, , -4中,最小的数是( )A、0 B、-π C、 D、-42. 下列图形中,不是正方体表面展开图的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列运算正确的是( )A、 B、 C、 D、4. 将一直角三角板与两边平行的纸条如图放置若∠1=60°,则∠2的度数为( )
3. 下列运算正确的是( )A、 B、 C、 D、4. 将一直角三角板与两边平行的纸条如图放置若∠1=60°,则∠2的度数为( )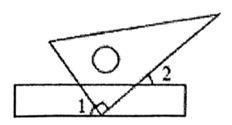 A、60° B、45° C、50° D、30°5. 若a,b满足 , 则( )A、3 B、4 C、5 D、66. 关于x的一元二次方程有实数根,则a的取值范围是( )A、或 B、 C、或 D、7. 如图,点A、B、C是⊙O上的三点,且四边形ABCO是平行四边形,OF⊥OC交圆O于点F,则∠BAF等于( )
A、60° B、45° C、50° D、30°5. 若a,b满足 , 则( )A、3 B、4 C、5 D、66. 关于x的一元二次方程有实数根,则a的取值范围是( )A、或 B、 C、或 D、7. 如图,点A、B、C是⊙O上的三点,且四边形ABCO是平行四边形,OF⊥OC交圆O于点F,则∠BAF等于( ) A、12.5° B、15° C、20° D、22.5°8. 如图,已知▱ABCD的面积为4,点P在AB边上从左向右运动(不含端点),设△APD的面积为x,△BPC的面积为y,则y关于x的函数图象大致是( )
A、12.5° B、15° C、20° D、22.5°8. 如图,已知▱ABCD的面积为4,点P在AB边上从左向右运动(不含端点),设△APD的面积为x,△BPC的面积为y,则y关于x的函数图象大致是( )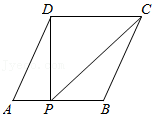 A、
A、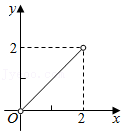 B、
B、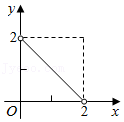 C、
C、 D、
D、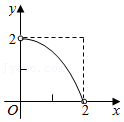 9. 如图,四边形ABCD为正方形,的平分线交BC于点E,将绕点B顺时针旋转90°得到 , 延长AE交CF于点G,连接BG,DG与AC相交于点H.有下列结论:①;②;③;④ , 其中正确的结论有( )个
9. 如图,四边形ABCD为正方形,的平分线交BC于点E,将绕点B顺时针旋转90°得到 , 延长AE交CF于点G,连接BG,DG与AC相交于点H.有下列结论:①;②;③;④ , 其中正确的结论有( )个 A、1 B、2 C、3 D、410. “分母有理化”是根式运算的一种化简方法,如:;除此之外,还可以用先平方再开方的方法化简一些有特点的无理数,如要化简 , 可以先设 , 再两边平方得 , 又因为 , 故x>0,解得 , , 根据以上方法,化简的结果是( )A、 B、 C、 D、3
A、1 B、2 C、3 D、410. “分母有理化”是根式运算的一种化简方法,如:;除此之外,还可以用先平方再开方的方法化简一些有特点的无理数,如要化简 , 可以先设 , 再两边平方得 , 又因为 , 故x>0,解得 , , 根据以上方法,化简的结果是( )A、 B、 C、 D、3二、填空题
-
11. 新型冠状病毒也叫2019-nCOV,该病毒比细胞小得多,大小约为(纳米),即为0.00000015米,约为一根头发丝直径的千分之一,数据0.00000015米用科学记数法表示为米.12. 因式分解: .13. 若 , 则等于 .14. 如图,矩形AOBC的顶点A、B在坐标轴上,点C的坐标是 , 点D在AC上,将沿BD翻折,点C恰好落在OA边上的点E处,则等于 .
 15. 如图所示,若用半径为8,圆心角为120°的扇形围成一个圆锥的侧面(接缝忽略不计),则这个圆锥的底面半径是.
15. 如图所示,若用半径为8,圆心角为120°的扇形围成一个圆锥的侧面(接缝忽略不计),则这个圆锥的底面半径是. 16. 请写出一个符合以下所有条件的一元二次方程:(1)二次项的系数为负数;(2)一个实数根为的整数部分,另一个实数根为-4,则这个一元二次方程可以是 . (任意写一个符合条件的即可).17. 如图,在中, , , , 以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最小值是 .
16. 请写出一个符合以下所有条件的一元二次方程:(1)二次项的系数为负数;(2)一个实数根为的整数部分,另一个实数根为-4,则这个一元二次方程可以是 . (任意写一个符合条件的即可).17. 如图,在中, , , , 以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最小值是 .
三、解答题
-
18. 求不等式组的整数解.19. 为弘扬中华传统文化、某校开展“戏剧进课堂”的活动.该校随机抽取部分学生,四个类别:A表示“很喜欢”,B表示“喜欢”,C表示“一般”,D表示“不喜欢”,调查他们对戏剧的喜爱情况,将结果绘制成如图两幅不完整的统计图,根据图中提供的信息.解决下列问题:
 (1)、此次共调查了名学生;(2)、扇形统计图中.B类所对应的扇形圆心角的大小为度;(3)、请通过计算补全条形统计图;(4)、该校共有1560名学生.估计该校表示“很喜欢”的A类的学生有多少人?20. 如图,已知 , 90°.
(1)、此次共调查了名学生;(2)、扇形统计图中.B类所对应的扇形圆心角的大小为度;(3)、请通过计算补全条形统计图;(4)、该校共有1560名学生.估计该校表示“很喜欢”的A类的学生有多少人?20. 如图,已知 , 90°. (1)、请用尺规作图,在BC边上找一点D,使;(不写作法,保留作图痕迹)(2)、在(1)的条件下,若 , , 求CD的值.21. 如图,在四边形ABCD中,90°,对角线AC,BD相交于点N.点M是对角线BD的中点,连接AM,CM.如果 , , 且 .
(1)、请用尺规作图,在BC边上找一点D,使;(不写作法,保留作图痕迹)(2)、在(1)的条件下,若 , , 求CD的值.21. 如图,在四边形ABCD中,90°,对角线AC,BD相交于点N.点M是对角线BD的中点,连接AM,CM.如果 , , 且 . (1)、求证:四边形AMCD是平行四边形;(2)、延长AM交BC于点E,求的值.22. 4月23日为“世界读书日”.每年的这一天,各地都会举办各种宣传活动.我市某书店为迎接“读书节”制定了活动计划,以下是活动计划书的部分信息:
(1)、求证:四边形AMCD是平行四边形;(2)、延长AM交BC于点E,求的值.22. 4月23日为“世界读书日”.每年的这一天,各地都会举办各种宣传活动.我市某书店为迎接“读书节”制定了活动计划,以下是活动计划书的部分信息:“读书节”活动计划书
图书类别
A类
B类
进价
18元/本
12元/本
备注
⑴用不超过16800元购进AB两类图书共1000本;
⑵A类图书不少于600本;
(1)、陈经理查看计划书时发现:A类图书的销售价是B类图书销售价的1.5倍,若顾客同样用54元购买图书,能购买A类图书数量比B类图书的数量少1本,求A、B两类图书的销售价;(2)、为了扩大影响,陈经理调整了销售方案:A类图书每本按原销售价降低2元销售,B类图书价格不变,那么该书店应如何进货才能获得最大利润?23. 如图,在平面直角坐标系中,矩形OABC的顶点B的坐标为 , OA,OC分别在x轴、y轴上,OB是矩形的对角线.将绕点O逆时针旋转,使点B落在y轴上,得到 , OD与CB相交于点F,反比例函数的图象经过点F,交AB于点G.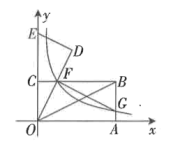 (1)、填空:k的值为;(2)、连接FG,求证:;(3)、在线段OA上找一点P,使得是等腰三角形,请直接写出此时OP的长.24. 如图,AB是O的直径,C、D是O上两点,且 , 过点D的直线交
(1)、填空:k的值为;(2)、连接FG,求证:;(3)、在线段OA上找一点P,使得是等腰三角形,请直接写出此时OP的长.24. 如图,AB是O的直径,C、D是O上两点,且 , 过点D的直线交AC的延长线于点E,交AB的延长线于点F,连接AD、OE交于点G.
 (1)、求证:DE是O的切线;(2)、若 , O的半径为2,求阴影部分的面积:(3)、连接BE,在(2)的条件下,求BE的长.25. 如图1,抛物线与x轴交于A,B两点,与y轴交于点C,直线BC的解析式为;线段OC的垂直平分线交抛物线于点M、N,点M、N横坐标分别为、且满足 .
(1)、求证:DE是O的切线;(2)、若 , O的半径为2,求阴影部分的面积:(3)、连接BE,在(2)的条件下,求BE的长.25. 如图1,抛物线与x轴交于A,B两点,与y轴交于点C,直线BC的解析式为;线段OC的垂直平分线交抛物线于点M、N,点M、N横坐标分别为、且满足 .
 (1)、求抛物线的解析式;(2)、设点Q是直线MN上一动点,当点Q在什么位置上时,的周长最小?求出此时点Q的坐标及周长的最小值;(3)、如图2,P是线段CB上的一点,过点P作直线轴于F,交抛物线于G,且;点H是直线BC上一个动点,点Q是坐标平面内一点,以点H,Q,P,F为顶点的四边形是菱形,直接写出所有满足条件的Q点坐标.
(1)、求抛物线的解析式;(2)、设点Q是直线MN上一动点,当点Q在什么位置上时,的周长最小?求出此时点Q的坐标及周长的最小值;(3)、如图2,P是线段CB上的一点,过点P作直线轴于F,交抛物线于G,且;点H是直线BC上一个动点,点Q是坐标平面内一点,以点H,Q,P,F为顶点的四边形是菱形,直接写出所有满足条件的Q点坐标.