广东省江门市新会区2022年中考模拟数学试题
试卷更新日期:2022-05-30 类型:中考模拟
一、单选题
-
1. 的相反数和倒数分别是( )A、3, B、3, C、-3, D、-3,2. 聪聪在阅读一篇文章时看到水分子的直径约为0.4纳米,通过百度搜索聪聪又知道1纳米 米,则水分子的直径约为( )A、 米 B、 米 C、 米 D、 米3. 已知点与点关于轴对称,则( )A、1 B、-1 C、-2021 D、20224. 已知 , , 那么( )A、17 B、54 C、72 D、815. 如图,要测量小河宽的距离,在河边取的垂线 , 在上取一点 , 使米时,量得 , 则小河宽PA=( )
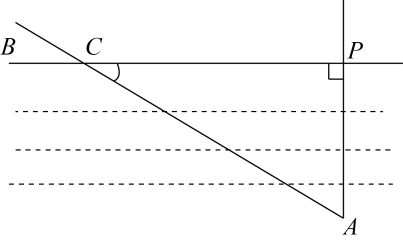 A、 B、 C、 D、6. 已知关于的一元二次方程有两个不相等的实数根,则实数的取值范围是( )A、 B、且 C、且 D、7. 如图,在 中, 平分 交 于点D, , ,则 的度数是( )
A、 B、 C、 D、6. 已知关于的一元二次方程有两个不相等的实数根,则实数的取值范围是( )A、 B、且 C、且 D、7. 如图,在 中, 平分 交 于点D, , ,则 的度数是( )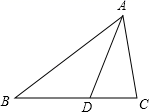 A、 B、 C、 D、8. 如图摆放的学生用直角三角板, , , 与相交于点 , 当时,的度数是( ).
A、 B、 C、 D、8. 如图摆放的学生用直角三角板, , , 与相交于点 , 当时,的度数是( ). A、 B、 C、 D、9. 已知正比例函数 的图象与反比例函数 图象相交于点 ,下列说法正确的是( )A、反比例函数 的解析式是 B、两个函数图象的另一交点坐标为 C、当 或 时, D、正比例函数 与反比例函数 都随 的增大而增大10. 一辆快车和一辆慢车将一批物资从甲地运往乙地,其中快车送达后停车卸货刚好一个小时,然后沿原路返回,且往返速度的大小不变,两车离甲地的距离(单位:)与慢车行驶时间(单位:)的函数关系如图,则两车先后两次相遇的间隔时间是( )
A、 B、 C、 D、9. 已知正比例函数 的图象与反比例函数 图象相交于点 ,下列说法正确的是( )A、反比例函数 的解析式是 B、两个函数图象的另一交点坐标为 C、当 或 时, D、正比例函数 与反比例函数 都随 的增大而增大10. 一辆快车和一辆慢车将一批物资从甲地运往乙地,其中快车送达后停车卸货刚好一个小时,然后沿原路返回,且往返速度的大小不变,两车离甲地的距离(单位:)与慢车行驶时间(单位:)的函数关系如图,则两车先后两次相遇的间隔时间是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
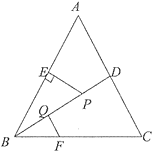
11. 化简: =.12. 分解因式: .13. 一个不透明的布袋中装有3个白球和个黄球,它们除了颜色不同外,其余均相同,若从中随机摸出一个球,摸到白球的概率是 , 则 .14. 如图,是等边三角形.是的平分线上一点,于点 , 线段的垂直平分线交于点 , 垂足为点 . 若 , 则的长为 .
 15. 把二次函数 的图象绕原点旋转180°后得到的图象解析式为 .
15. 把二次函数 的图象绕原点旋转180°后得到的图象解析式为 .
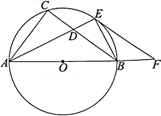
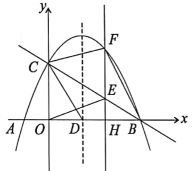
16. 如图,在半径为5的⊙O中,弦AB=6,点C是优弧 上一点(不与A,B重合),则cosC的值为 .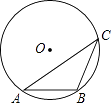 17. 如图,在平面直角坐标系中,点、在函数的图象上,过点作轴的垂线,与函数的图象交于点 , 连结交轴于点 , 若点的横坐标为1,且 , 则点的横坐标是 .
17. 如图,在平面直角坐标系中,点、在函数的图象上,过点作轴的垂线,与函数的图象交于点 , 连结交轴于点 , 若点的横坐标为1,且 , 则点的横坐标是 .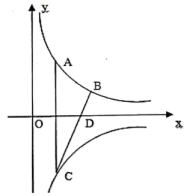
三、解答题
-
18. 先化简,再求值: , 其中 .19. 解方程: .20. 如图, 中, , , .
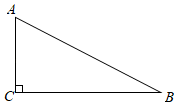 (1)、用直尺和圆规作 的垂直平分线;(保留作图痕迹,不要求写作法)(2)、若(1)中所作的垂直平分线交 于点 ,求 的长.21. 某中学现有在校学生2800人,学校为了解本校学生的课余活动情况,采取随机抽样的方法从阅读、运动、娱乐、其它四个方面调查了若干名学生,并将调查的结果绘制了如下两幅不完整的统计图,请根据图中提供的信息解答下列问题:
(1)、用直尺和圆规作 的垂直平分线;(保留作图痕迹,不要求写作法)(2)、若(1)中所作的垂直平分线交 于点 ,求 的长.21. 某中学现有在校学生2800人,学校为了解本校学生的课余活动情况,采取随机抽样的方法从阅读、运动、娱乐、其它四个方面调查了若干名学生,并将调查的结果绘制了如下两幅不完整的统计图,请根据图中提供的信息解答下列问题: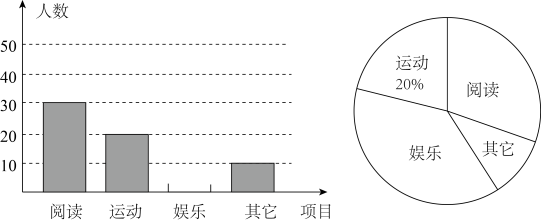 (1)、在这次随机抽样中,一共调查了多少名学生?(2)、通过计算补全条形图,并求出扇形统计图中阅读部分的扇形圆心角的度数;(3)、请你估计该中学在课余时间参加阅读和其它活动的学生一共有多少名.22. 数学课外活动小组进行如下操作实验,把一根长的铁丝剪成两段.(1)、把每段首尾相连各围成一个正方形.要使这两个正方形的面积之和等于 , 应该怎么剪这根铁丝?(2)、若把剪成两段的铁丝围成两个圆,两圆面积之和的最小值是多少?23. 如图,在△ABC中, D是AC的中点,E是线段BC延长线上一点,过点A作交ED的延长线于点F,连接AE, CF.求证:
(1)、在这次随机抽样中,一共调查了多少名学生?(2)、通过计算补全条形图,并求出扇形统计图中阅读部分的扇形圆心角的度数;(3)、请你估计该中学在课余时间参加阅读和其它活动的学生一共有多少名.22. 数学课外活动小组进行如下操作实验,把一根长的铁丝剪成两段.(1)、把每段首尾相连各围成一个正方形.要使这两个正方形的面积之和等于 , 应该怎么剪这根铁丝?(2)、若把剪成两段的铁丝围成两个圆,两圆面积之和的最小值是多少?23. 如图,在△ABC中, D是AC的中点,E是线段BC延长线上一点,过点A作交ED的延长线于点F,连接AE, CF.求证: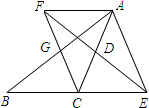 (1)、四边形AFCE是平行四边形:(2)、 .
(1)、四边形AFCE是平行四边形:(2)、 .