广东省佛山顺德区2022年九年级下学期第二次教学质量检测数学试题(二模)
试卷更新日期:2022-05-30 类型:中考模拟
一、单选题
-
1. 实数中,最小的数是( )A、-1 B、 C、0 D、2. 神舟十三号从距离地面约390千米空间站返回.将390千米用科学记数法表示为( )米A、 B、 C、 D、3. 在中,对角线 , 相交于点 , 下列结论一定正确的是( )A、 B、 C、 D、4. 如图是一个游戏转盘,自由转动转盘,当转盘停止转动后,指针落在数字“Ⅱ”所示区域内的概率是( )
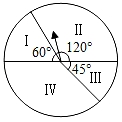 A、 B、 C、 D、5. 计算:( )A、 B、 C、-4 D、46. 如图是一个几何体的三视图,对这个几何体的描述正确的是( )
A、 B、 C、 D、5. 计算:( )A、 B、 C、-4 D、46. 如图是一个几何体的三视图,对这个几何体的描述正确的是( )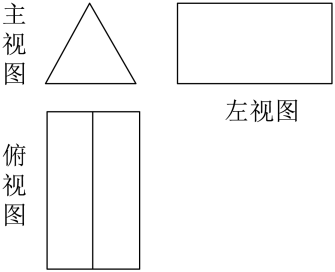 A、底面是长方形 B、侧面是三角形 C、三棱柱 D、四棱柱7. 不等式组 的解集在数轴上表示正确的是( )A、
A、底面是长方形 B、侧面是三角形 C、三棱柱 D、四棱柱7. 不等式组 的解集在数轴上表示正确的是( )A、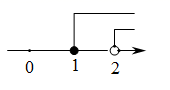 B、
B、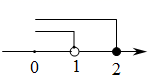 C、
C、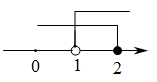 D、
D、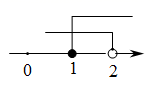 8. 一根钢管放在形架内,横截面如图所示,钢管的半径是6,若 , 则阴影部分的面积是( )
8. 一根钢管放在形架内,横截面如图所示,钢管的半径是6,若 , 则阴影部分的面积是( ) A、 B、 C、 D、9. 命题:已知 , . 求证: . 运用反证法证明这个命题时,第一步应假设( )成立A、 B、 C、 D、且10. 如图,的两条弦 , 互相垂直,垂足为 , 直径交线段于点 , 且 , 点是的中点.下列结论正确的个数是( )
A、 B、 C、 D、9. 命题:已知 , . 求证: . 运用反证法证明这个命题时,第一步应假设( )成立A、 B、 C、 D、且10. 如图,的两条弦 , 互相垂直,垂足为 , 直径交线段于点 , 且 , 点是的中点.下列结论正确的个数是( )①;②;③是等腰三角形;④ .
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 计算:( +1)( ﹣1)= .12. 如图,点A,B,C在直线l上,PB⊥l , PA=6cm,PB=5cm,PC=7cm,则点P到直线l的距离是cm.
 13. 方程的解为 .14. 一组数据2,3,x , 5,7的平均数是4,则这组数据的众数是15. 在中, , , 是的中点, , 则 .
13. 方程的解为 .14. 一组数据2,3,x , 5,7的平均数是4,则这组数据的众数是15. 在中, , , 是的中点, , 则 .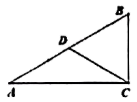 16. 化简; ÷( ﹣1)= .
16. 化简; ÷( ﹣1)= .
17. 若等腰三角形一腰上的高与另一腰的夹角为48°,则底角的度数为 .三、解答题
-
18. 关于的一元二次方程 .(1)、当时,解方程;(2)、当方程有两个不相等的实数根时,求的取值范围.19. 如图,在中, , 平分交于点 , 过点作于点 .
 (1)、求证:;(2)、当 , , 时,求的正切值.20. 第24届冬季奥林匹克运动会于2022年2月4日至20日在北京市和张家口市联合举行,这是中国第一次举办冬季奥运会.北京冬季奥运会的成功举办,激发了国人对冰雪运动项目的喜爱热潮.某中学为了解学生对速度滑冰、冰球、单板滑雪、高山滑雪、冰壶的喜爱情况,在全校范围内随机抽取了若干名学生进行问卷调查,数据如下:
(1)、求证:;(2)、当 , , 时,求的正切值.20. 第24届冬季奥林匹克运动会于2022年2月4日至20日在北京市和张家口市联合举行,这是中国第一次举办冬季奥运会.北京冬季奥运会的成功举办,激发了国人对冰雪运动项目的喜爱热潮.某中学为了解学生对速度滑冰、冰球、单板滑雪、高山滑雪、冰壶的喜爱情况,在全校范围内随机抽取了若干名学生进行问卷调查,数据如下:项目
速度滑冰
冰球
单板滑雪
高山滑雪
冰壶
人数
50
24
80
16
 (1)、喜爱高山滑雪的人数a=;单板滑雪所在的圆心角度数为;(2)、学校针对冰雪运动项目进行了班级知识竞赛,每班由5名学生组成.其中班学生的竞赛得分为:85,75,80,82,78,方差为;班学生的竞赛得分为76,80,82,84,78,方差为 , 判断哪个班的成绩更稳定?为什么?(方差公式)21. 某种消毒药喷洒释放完毕开始计时,药物浓度与时间之间的关系如下:
(1)、喜爱高山滑雪的人数a=;单板滑雪所在的圆心角度数为;(2)、学校针对冰雪运动项目进行了班级知识竞赛,每班由5名学生组成.其中班学生的竞赛得分为:85,75,80,82,78,方差为;班学生的竞赛得分为76,80,82,84,78,方差为 , 判断哪个班的成绩更稳定?为什么?(方差公式)21. 某种消毒药喷洒释放完毕开始计时,药物浓度与时间之间的关系如下:时间
2
4
12
药物浓度
18
9
3
(1)、求关于的关系式;(2)、当药物浓度不低于并且持续时间不少于时消毒算有效,问这次消毒是否有效?.22. 如图,的半径为4,点在上. (1)、尺规作图:过点作的切线;(2)、在(1)的条件下,点是上的一个动点(不与点重合),过点作于点 , 连接 . 设 , , 求的最大值.23. 平面直角坐标系中有两个一次函数 , , 其中的图象与轴交点的横坐标为2且经过点(1,2), .(1)、求函数的关系式;(2)、当的图象经过两点和时,求的值;(3)、当时,对于的每一个值,都有 , 求的取值范围.24. 如图
(1)、尺规作图:过点作的切线;(2)、在(1)的条件下,点是上的一个动点(不与点重合),过点作于点 , 连接 . 设 , , 求的最大值.23. 平面直角坐标系中有两个一次函数 , , 其中的图象与轴交点的横坐标为2且经过点(1,2), .(1)、求函数的关系式;(2)、当的图象经过两点和时,求的值;(3)、当时,对于的每一个值,都有 , 求的取值范围.24. 如图 (1)、动手操作:如图1,将一张长方形的纸对折两次,然后沿45°的方向剪下一个角,打开,剪出的是一个形.再利用图形的“旋转”开展数学探究活动,体会图形在旋转过程中的变化及其蕴含的数学思想方法;(2)、问题探究:如图2,由“动手操作”所得的四边形的对角线相交于点 , 把一个与它全等的四边形绕点旋转,交于 , 交于 . 探究线段 , 之间的数量关系,并说明理由;(3)、拓展迁移:如图3,矩形的对角线交点为 , 直角的边 , 分别与边 , 相交于 , . 设(为常数),探究线段 , 之间的数量关系,并说明理由.25. 如图,在中, , , . 在它的内部作一个矩形 , 使得在边上,、分别在边、上.设 , 矩形的面积为 .
(1)、动手操作:如图1,将一张长方形的纸对折两次,然后沿45°的方向剪下一个角,打开,剪出的是一个形.再利用图形的“旋转”开展数学探究活动,体会图形在旋转过程中的变化及其蕴含的数学思想方法;(2)、问题探究:如图2,由“动手操作”所得的四边形的对角线相交于点 , 把一个与它全等的四边形绕点旋转,交于 , 交于 . 探究线段 , 之间的数量关系,并说明理由;(3)、拓展迁移:如图3,矩形的对角线交点为 , 直角的边 , 分别与边 , 相交于 , . 设(为常数),探究线段 , 之间的数量关系,并说明理由.25. 如图,在中, , , . 在它的内部作一个矩形 , 使得在边上,、分别在边、上.设 , 矩形的面积为 .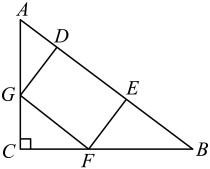 (1)、写出图中的一对相似三角形;(2)、写出关于的函数关系式;(3)、若、是平面直角坐标系中的两个点,判断线段MN与(2)中函数图象的交点情况,并求出对应m的取值范围.
(1)、写出图中的一对相似三角形;(2)、写出关于的函数关系式;(3)、若、是平面直角坐标系中的两个点,判断线段MN与(2)中函数图象的交点情况,并求出对应m的取值范围.