北京市东城区2022年中考一模数学试题
试卷更新日期:2022-05-30 类型:中考模拟
一、单选题
-
1. 下列立体图形中,主视图是圆的是( )A、
 B、
B、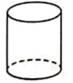 C、
C、 D、
D、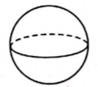 2. 国家统计局发布2021年国内生产总值达到1140000亿元,比上年增长8.1%.将1140000用科学记数法表示应为( )A、 B、 C、 D、3. 如图,将一块直角三角板的直角顶点放在直尺的一边上.若∠2=40°,则∠1的度数是( )
2. 国家统计局发布2021年国内生产总值达到1140000亿元,比上年增长8.1%.将1140000用科学记数法表示应为( )A、 B、 C、 D、3. 如图,将一块直角三角板的直角顶点放在直尺的一边上.若∠2=40°,则∠1的度数是( ) A、60° B、50° C、40° D、30°4. 七巧板是我国古代劳动人民的发明之一,被誉为“东方魔板”.将右图的七巧板的其中几块,拼成一个多边形,为轴对称图形的是( )
A、60° B、50° C、40° D、30°4. 七巧板是我国古代劳动人民的发明之一,被誉为“东方魔板”.将右图的七巧板的其中几块,拼成一个多边形,为轴对称图形的是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 五边形的内角和是( )A、 B、 C、 D、6. 实数a,b在数轴上对应的点的位置如图所示,下列结论正确的是( )
5. 五边形的内角和是( )A、 B、 C、 D、6. 实数a,b在数轴上对应的点的位置如图所示,下列结论正确的是( )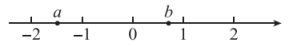 A、 B、 C、 D、7. 某班甲、乙、丙三位同学5次数学成绩及班级平均分的折线统计图如下,则下列判断错误的是( )
A、 B、 C、 D、7. 某班甲、乙、丙三位同学5次数学成绩及班级平均分的折线统计图如下,则下列判断错误的是( ) A、甲的数学成绩高于班级平均分 B、乙的数学成绩在班级平均分附近波动 C、丙的数学成绩逐次提高 D、甲、乙、丙三人中,甲的数学成绩最不稳定8. 将一圆柱形小水杯固定在大圆柱形容器底面中央,现用一个注水管沿大容器内壁匀速注水,如图所示,则小水杯水面的高度与注水时间的函数图象大致是( )
A、甲的数学成绩高于班级平均分 B、乙的数学成绩在班级平均分附近波动 C、丙的数学成绩逐次提高 D、甲、乙、丙三人中,甲的数学成绩最不稳定8. 将一圆柱形小水杯固定在大圆柱形容器底面中央,现用一个注水管沿大容器内壁匀速注水,如图所示,则小水杯水面的高度与注水时间的函数图象大致是( )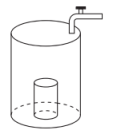 A、
A、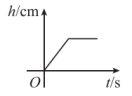 B、
B、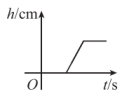 C、
C、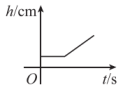 D、
D、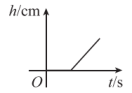
二、填空题
-
9. 若 在实数范围内有意义,则实数x的取值范围是 .10. 分解因式: = .11. 方程 的解是 .12. 请写出一个大于1且小于2的无理数:.13. 北京2022年冬奥会和冬残奥会的吉祥物“冰墩墩”和“雪容融”广受大家的喜爱.即将在2022年9月举行的杭州亚运会的吉祥物“宸宸”“踪踪”“莲莲”也引起了大家的关注.现将五张正面分别印有以上5个吉祥物图案的卡片(卡片的形状、大小、质地都相同)背面朝上并洗匀,随机翻开一张正好是“冰墩墩”的概率是 .
 14. 如图,点A,B,C是⊙O上的三点.若∠AOC=90°,∠BAC=30°,则∠AOB的度数为 .
14. 如图,点A,B,C是⊙O上的三点.若∠AOC=90°,∠BAC=30°,则∠AOB的度数为 . 15. 已知 , 则代数式 .16. 我国古代天文学和数学著作《周髀算经》中提到:一年有二十四个节气,每个节气的晷(ɡuǐ)长损益相同(晷是按照日影测定时刻的仪器,晷长即为所测量影子的长度),二十四节气如图所示.从冬至到夏至晷长逐渐变小,从夏至到冬至晷长逐渐变大,相邻两个节气晷长减少或增加的量均相同,周而复始.若冬至的晷长为13.5尺,夏至的晷长为1.5尺,则相邻两个节气晷长减少或增加的量为尺,立夏的晷长为尺.
15. 已知 , 则代数式 .16. 我国古代天文学和数学著作《周髀算经》中提到:一年有二十四个节气,每个节气的晷(ɡuǐ)长损益相同(晷是按照日影测定时刻的仪器,晷长即为所测量影子的长度),二十四节气如图所示.从冬至到夏至晷长逐渐变小,从夏至到冬至晷长逐渐变大,相邻两个节气晷长减少或增加的量均相同,周而复始.若冬至的晷长为13.5尺,夏至的晷长为1.5尺,则相邻两个节气晷长减少或增加的量为尺,立夏的晷长为尺.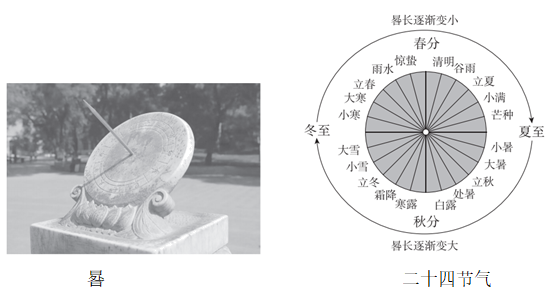
三、解答题
-
17. 计算: .18. 解不等式组 .19. 已知:线段AB.

求作: , 使得 , .
作法:
①分别以点A和点B为圆心,AB长为半径作弧,两弧交于点D;
②连接BD,在BD的延长线上截取;
③连接AC.
则为所求作的三角形.
(1)、使用直尺和圆规,依作法补全图形(保留作图痕迹);(2)、完成下面的证明.证明:连接AD.
∵ ,
∴为等边三角形( ).(填推理的依据)
∴ .
∵ ,
∴ .
∴ ▲ ( ).(填推理的依据)
∴ .
∴ .
在中,
∴ .
20. 已知关于x的一元二次方程有两个不相等的实数根.(1)、求k的取值范围;(2)、若k为正整数,且方程的两个根均为整数,求k的值及方程的两个根.21. 在平面直角坐标系中,一次函数的图象与x轴交于点A,与反比例函数的图象交于点 , 点P为反比例函数的图象上一点.(1)、求m,k的值;(2)、连接OP,AP.当时,求点P的坐标.22. 如图,在四边形ABCD中,AC与BD相交于点O,且 , 点E在BD上, . (1)、求证:四边形AECD是平行四边形;(2)、若 , , , , 求BE的长.23. 如图,在中, , 以AB为直径作 , 交BC于点D,交AC于点E,过点B作的切线交OD的延长线于点F.
(1)、求证:四边形AECD是平行四边形;(2)、若 , , , , 求BE的长.23. 如图,在中, , 以AB为直径作 , 交BC于点D,交AC于点E,过点B作的切线交OD的延长线于点F. (1)、求证:;(2)、若 , , 求AE的长.24. 2022年是中国共产主义青年团建团100周年.某校举办了一次关于共青团知识的竞赛,七、八年级各有300名学生参加了本次活动,为了解两个年级的答题情况,从两个年级各随机抽取了20名学生的成绩进行调查分析.下面给出了部分信息:
(1)、求证:;(2)、若 , , 求AE的长.24. 2022年是中国共产主义青年团建团100周年.某校举办了一次关于共青团知识的竞赛,七、八年级各有300名学生参加了本次活动,为了解两个年级的答题情况,从两个年级各随机抽取了20名学生的成绩进行调查分析.下面给出了部分信息:a.七年级学生的成绩整理如下(单位:分):
57 67 69 75 75 75 77 77 78 78 80 80 80 80 86 86 88 88 89 96
b.八年级学生成绩的频数分布直方图如下(数据分成四组: , , , ):

其中成绩在的数据如下(单位:分):
80 80 81 82 83 84 85 86 87 89
c.两组样本数据的平均数、中位数、众数如下表所示:
年级
平均数
中位数
众数
七年级
79.05
79
m
八年级
79.2
n
74
根据所给信息,解答下列问题:
(1)、 , ;(2)、估计年级学生的成绩高于平均分的人数更多;(3)、若成绩达到80分及以上为优秀,估计七年级和八年级此次测试成绩优秀的总人数.25. 某公园内人工湖上有一座拱桥(横截面如图所示),跨度AB为4米.在距点A水平距离为d米的地点,拱桥距离水面的高度为h米.小红根据学习函数的经验,对d和h之间的关系进行了探究.
下面是小红的探究过程,请补充完整:
(1)、经过测量,得出了d和h的几组对应值,如下表.d/米
0
0.6
1
1.8
2.4
3
3.6
4
h/米
0.88
1.90
2.38
2.86
2.80
2.38
1.60
0.88
在d和h这两个变量中,是自变量,是这个变量的函数;
(2)、在下面的平面直角坐标系中,画出(1)中所确定的函数的图象; (3)、结合表格数据和函数图象,解决问题:
(3)、结合表格数据和函数图象,解决问题:①桥墩露出水面的高度AE为米;
②公园欲开设游船项目,现有长为3.5米,宽为1.5米,露出水面高度为2米的游船.为安全起见,公园要在水面上的C,D两处设置警戒线,并且 , 要求游船能从C,D两点之间安全通过,则C处距桥墩的距离CE至少为米.(精确到0.1米)
 26. 在平面直角坐标系中,抛物线与y轴交于点A.点是抛物线上的任意一点,且不与点A重合,直线经过A,B两点.(1)、求抛物线的顶点坐标(用含m的式子表示);(2)、若点 , 在抛物线上,则a b(用“<”,“=”或“>”填空);(3)、若对于时,总有 , 求m的取值范围.27. 如图,在正方形ABCD中,E为对角线AC上一点(),连接BE,DE.
26. 在平面直角坐标系中,抛物线与y轴交于点A.点是抛物线上的任意一点,且不与点A重合,直线经过A,B两点.(1)、求抛物线的顶点坐标(用含m的式子表示);(2)、若点 , 在抛物线上,则a b(用“<”,“=”或“>”填空);(3)、若对于时,总有 , 求m的取值范围.27. 如图,在正方形ABCD中,E为对角线AC上一点(),连接BE,DE. (1)、求证:;(2)、过点E作交BC于点F,延长BC至点G,使得 , 连接DG.
(1)、求证:;(2)、过点E作交BC于点F,延长BC至点G,使得 , 连接DG.①依题意补全图形;
②用等式表示BE与DG的数量关系,并证明.
28. 对于平面直角坐标系中的点C及图形G,有如下定义:若图形G上存在A,B两点,使得为等腰直角三角形,且 , 则称点C为图形G的“友好点”.(1)、已知点 , , 在点 , , 中,线段OM的“友好点”是;(2)、直线分别交x轴、y轴于P,Q两点,若点为线段PQ的“友好点”,求b的取值范围;(3)、已知直线分别交x轴、y轴于E,F两点,若线段EF上的所有点都是半径为2的的“友好点”,直接写出d的取值范围.