安徽省马鞍山市雨山区2022年第二次中考模拟考试数学试题
试卷更新日期:2022-05-30 类型:中考模拟
一、单选题
-
1. 在-2,1,0, 中,其绝对值最大的数是( )A、-2 B、1 C、0 D、2. 下列运算正确的是()A、 B、 C、 D、3. 2020年是及其不平凡的一年,年初席卷全国的新冠疫情让全国上下都把全部注意力投向了卫生防疫方面,但是具有大无畏精神的安徽人民等到疫情局势稳定下来之后,就积极地恢复了各行各业的生产,从而创造了人间奇迹.安徽GDP正式发布,安徽省全年生产总值约3.88万亿元.其中“3.88万亿”用科学记数法可以表示为()A、 B、 C、 D、4. 如图,是放置在北京冬奥会场馆内水平地面上的领奖台,其几何体左视图是( )
 A、
A、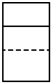 B、
B、 C、
C、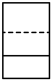 D、
D、 5. 一副三角板按如图所示的位置摆放,若BC∥DE,则∠1的度数是( )
5. 一副三角板按如图所示的位置摆放,若BC∥DE,则∠1的度数是( )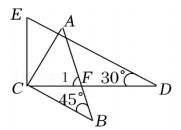 A、65° B、70° C、75° D、80°6. 已知圆锥的底面半径为4,母线长为6,则它的侧面展开图的面积是( )A、24 B、48 C、12 D、247. 若关于x的一元二次方程(x﹣2)(x﹣3)=m有实数根x1 , x2 , 且x1≠x2 , 则m的取值范围是( )A、m>﹣ B、m<﹣ C、m≥﹣ D、m≤﹣8. 如图,在 中,点 , 分别在 , 边上, , ,若 , ,则线段 的长为( )
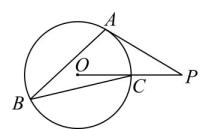
A、65° B、70° C、75° D、80°6. 已知圆锥的底面半径为4,母线长为6,则它的侧面展开图的面积是( )A、24 B、48 C、12 D、247. 若关于x的一元二次方程(x﹣2)(x﹣3)=m有实数根x1 , x2 , 且x1≠x2 , 则m的取值范围是( )A、m>﹣ B、m<﹣ C、m≥﹣ D、m≤﹣8. 如图,在 中,点 , 分别在 , 边上, , ,若 , ,则线段 的长为( )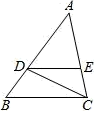 A、 B、 C、 D、59. 如图,A、B表示足球门边框(不考虑球门的高度)的两个端点,点C表示射门点,连接AC、BC,则∠ACB就是射门角,在不考虑其它因素的情况下,一般射门角越大,射门进球的可能性就越大,球员甲带球线路ED与球门AB垂直,D为垂足,点C在ED上,当∠ACB最大时就是带球线路ED上的最佳射门角,若AB=4,BD=1,则当球员甲在此次带球中获得最佳射门角时DC的长度为( )
A、 B、 C、 D、59. 如图,A、B表示足球门边框(不考虑球门的高度)的两个端点,点C表示射门点,连接AC、BC,则∠ACB就是射门角,在不考虑其它因素的情况下,一般射门角越大,射门进球的可能性就越大,球员甲带球线路ED与球门AB垂直,D为垂足,点C在ED上,当∠ACB最大时就是带球线路ED上的最佳射门角,若AB=4,BD=1,则当球员甲在此次带球中获得最佳射门角时DC的长度为( )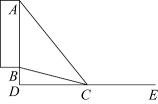 A、2 B、3 C、 D、10. 如图,正方形 的边长为 ,动点 , 同时从点 出发,在正方形的边上,分别按 , 的方向,都以 的速度运动,到达点 运动终止,连接 ,设运动时间为 , 的面积为 ,则下列图象中能大致表示 与 的函数关系的是( )
A、2 B、3 C、 D、10. 如图,正方形 的边长为 ,动点 , 同时从点 出发,在正方形的边上,分别按 , 的方向,都以 的速度运动,到达点 运动终止,连接 ,设运动时间为 , 的面积为 ,则下列图象中能大致表示 与 的函数关系的是( )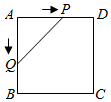 A、
A、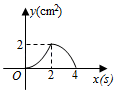 B、
B、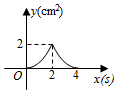 C、
C、 D、
D、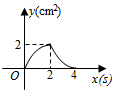
二、填空题
-
11. 若 ,则 .12. 分解因式: .13. 如图,已知⊙上有三点 , , , 半径 , , 切线交延长线于点 , 则的周长为 .
 14. 如图,在中, , , , 点是内部的一个动点,连接 , 且满足 , 过点作交于点 .
14. 如图,在中, , , , 点是内部的一个动点,连接 , 且满足 , 过点作交于点 . (1)、;(2)、当线段最短时,的面积为 .
(1)、;(2)、当线段最短时,的面积为 .三、解答题
-
15. 计算: .16. 《九章算术》中有这样一个问题:“今有五雀、六燕,集称之衡,雀俱重,燕俱轻.一雀一燕交而处,衡适平.并燕、雀重一斤.问燕、雀一枚各重几何?其大意如下:今有5只雀、6只燕,分别放一起用衡器称,聚在一起的雀重,燕轻.将1只雀、1只燕交换位置放,两边重量相等.5只雀、6只燕重量为1斤(注:声代1斤=16两).问每只雀、燕各重多少两?17. 2022年北京冬奥会开幕式主火炬台由96块小雪花形态和6块橄榄枝构成的巨型“雪花”形态,在数学上,我们可以通过“分形”近似地得到雪花的形状.操作:将一个边长为1的等边三角形(如图①)的每一边三等分,以居中那条线段为底边向外作等边三角形,并去掉所作的等边三角形的一条边,得到一个六角星(如图②,称为第一次分形.接着对每个等边三角形凸出的部分继续上述过程,即在每条边三等分后的中段向外画等边三角形,得到一个新的图形(如图③),称为第二次分形.不断重复这样的过程,就得到了“科赫雪花曲线”.
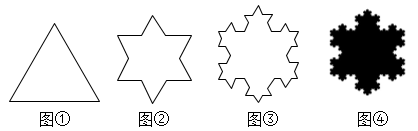 (1)、【规律总结】每一次分形后,得到的“雪花曲线”的边数是前一个“雪花曲线”边数的倍;每一次分形后,三角形的边长都变为原来的倍;(2)、【问题解决】试猜想第n次分形后所得图形的边数是;周长为(用含n的代数式表示)18. 如图,在边长为1的正方形网格中,的顶点均在格点上,点 , 的坐标分别是 , , 把绕点逆时针旋转后得到 .
(1)、【规律总结】每一次分形后,得到的“雪花曲线”的边数是前一个“雪花曲线”边数的倍;每一次分形后,三角形的边长都变为原来的倍;(2)、【问题解决】试猜想第n次分形后所得图形的边数是;周长为(用含n的代数式表示)18. 如图,在边长为1的正方形网格中,的顶点均在格点上,点 , 的坐标分别是 , , 把绕点逆时针旋转后得到 .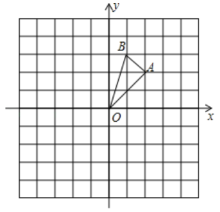
⑴画出 , 直接写出点 , 的坐标;
⑵计算在旋转过程中,所扫过的面积.
⑶以原点为位似中心,位似比为2,在第三象限画出放大后的 .
19. 校车安全是近几年社会关注的热门话题,其中超载和超速行驶是校车事故的主要原因.小亮和同学尝试用自己所学的三角函数知识检测校车是否超速,如下图,观测点设在到白田路的距离为100米的点P处.这时,一辆校车由西向东匀速行驶,测得此校车从A处行驶到B处所用的时间为4秒,且∠APO=60°,∠BPO =45°. (1)、求A、B之间的路程;(参考数据: , )(2)、请判断此校车是否超过了白田路每小时60千米的限制速度?20. 如图,在 中, ,D是AB上一点,⊙O经过点A、C、D,交BC于点E,过点D作 ,交⊙O于点F,求证:
(1)、求A、B之间的路程;(参考数据: , )(2)、请判断此校车是否超过了白田路每小时60千米的限制速度?20. 如图,在 中, ,D是AB上一点,⊙O经过点A、C、D,交BC于点E,过点D作 ,交⊙O于点F,求证: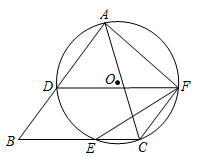 (1)、四边形DBCF是平行四边形(2)、21. 某校初三一班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
(1)、四边形DBCF是平行四边形(2)、21. 某校初三一班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):甲队
7
8
9
7
10
10
9
10
10
10
乙队
10
8
7
9
8
10
10
9
10
9
(1)、甲队成绩的中位数是分,乙队成绩的众数是分;(2)、已知甲队成绩的方差是1.4分2 , 则成绩较为整齐的是队;(3)、测试结果中,乙队获满分的四名同学相当优秀,他们是三名男生、一名女生,现准备从这四名同学中随机抽取两人参加学校组织的经典诵读比赛,用树状图或列表法求恰好抽中一男生一女生的概率.22. 合肥市某公司购进某种水果的成本为20元/kg,经过市场调研发现,这种水果在未来24天的销售单价p(元/kg)与时间t(天)之间的函数关系式p=t+30(t为整数),且其日销售量y(kg)与时间t(天)的函数关系如下表.时间t(天)
1
3
6
10
20
…
日销售量y(kg)
118
114
108
100
80
…
(1)、已知y与t之间的变化规律符合一次函数关系,试求此一次函数的解析式;(2)、问哪一天的销售利润最大?最大日销售利润为多少?(3)、在实际销售中,公司决定每销售1kg水果就捐赠n(n<9)元给“精准扶贫”对象.现发现:每天扣除捐赠后的日利润随时间t的增大而增大,求n的取值范围.23. 已知:如图1,中, , , 点是上一点,其中 , 将沿所在的直线折叠得到 , 交于 , 连接 .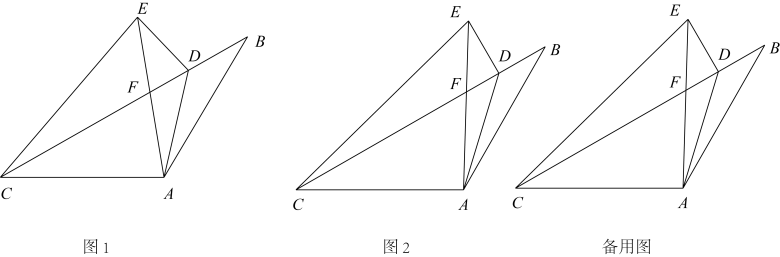 (1)、①当时, .
(1)、①当时, .②当时,(用含的代数式表示);
(2)、如图2,当时,解决以下问题:①已知 , 求的值;
②证明: .