安徽省淮南市东部地区2022年第一次中考模拟数学试题
试卷更新日期:2022-05-30 类型:中考模拟
一、单选题
-
1. -2的相反数是( )A、2 B、-2 C、 D、2. 某几何体的左视图如图所示,则该几何体不可能是( )
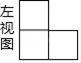 A、
A、 B、
B、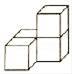 C、
C、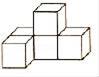 D、
D、 3. 下列各式一定成立的是( )A、a6÷a2=a3 B、(a﹣b)2=a2﹣b2 C、2a+3b=5ab D、(3a3)2 =9a64. 如图,a∥b,∠1=70°,则∠2等于( )
3. 下列各式一定成立的是( )A、a6÷a2=a3 B、(a﹣b)2=a2﹣b2 C、2a+3b=5ab D、(3a3)2 =9a64. 如图,a∥b,∠1=70°,则∠2等于( )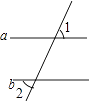 A、20° B、35° C、70° D、110°5. 2020年7月23日,中国首次火星探测任务“天问一号”探测器在海南文昌航天发射场由长征五号遥四运载火箭发射升空,每天基本飞行200万千米,并于2021年5月15日成功着陆预选区,火星上首次留下了中国的足迹.将200万用科学记数法表示为( )A、 B、 C、 D、6. 若关于x的一元二次方程没有实数根,则m的取值范围是( ).A、 B、 C、 D、7. 若直线y=﹣x+a与直线y=x+b的交点坐标为(2,8),则a﹣b的值为( )
A、20° B、35° C、70° D、110°5. 2020年7月23日,中国首次火星探测任务“天问一号”探测器在海南文昌航天发射场由长征五号遥四运载火箭发射升空,每天基本飞行200万千米,并于2021年5月15日成功着陆预选区,火星上首次留下了中国的足迹.将200万用科学记数法表示为( )A、 B、 C、 D、6. 若关于x的一元二次方程没有实数根,则m的取值范围是( ).A、 B、 C、 D、7. 若直线y=﹣x+a与直线y=x+b的交点坐标为(2,8),则a﹣b的值为( )
A、2 B、4 C、6 D、88. 国家统计局统计数据 显示,我国快递业务收入逐年增加.2017年至2019年我国快递业务收入由5000亿元增加到7500亿元.设我国2017年至2019年快递业务收入的年平均增长率为x.则可列方程为( )A、 B、 C、 D、9. 如图,在 中, .边 在x轴上,顶点 的坐标分别为 和 .将正方形 沿x轴向右平移当点E落在 边上时,点D的坐标为( )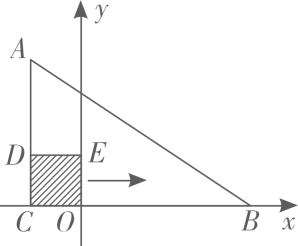 A、 B、 C、 D、10. 如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B,图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为( )
A、 B、 C、 D、10. 如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B,图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为( )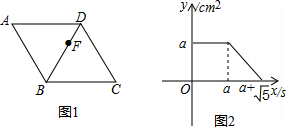 A、 B、2 C、 D、2
A、 B、2 C、 D、2二、填空题
-
11. 计算: .12. 分解因式:2a2+4a+2= .13. 如图,点M是函数y= x与y= 的图象在第一象限内的交点,OM=4,则k的值为 .
 14. 如图,在扇形BOC中, , OD平分交弧BC于点D.点E为半径OB上一动点,若 , 则长的最小值为 .
14. 如图,在扇形BOC中, , OD平分交弧BC于点D.点E为半径OB上一动点,若 , 则长的最小值为 .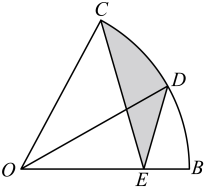
三、解答题
-
15. 先化简,再求值: ,其中16. 观察以下等式:
第1个等式:;
第2个等式:;
第3个等式:;
第4个等式:;
第5个等式:;
按照以上规律,解决下列问题:
(1)、写出第6个等式:;(2)、写出你猜想的第个等式: ▲ 用含的等式表示 , 并证明.17. 一家超市中,杏的售价为11元/kg,桃的售价为10元/kg,小菲在这家超市买了杏和桃共8kg,共花费83元,求小菲这次买的杏、桃各多少千克?18. 如图,在由边长为1个单位长度的小正方形组成的网格中,已知的顶点都在格点上,直线l与网线重合.
⑴以直线l为对称轴,画出关于l对称的;
⑵将向右平移10个单位长度,再向上平移1个单位长度,得到 , 画出;
⑶连接 , , 直接判断四边形的形状.
19. 位于河南省登封市境内的元代观星台,是中国现存最早的天文台,也是世界文化遗产之一.某校数学社团的同学们使用卷尺和自制的测角仪测量观星台的高度.如图所示,他们在地面一条水平步道MP上架设测角仪,先在点M处测得观星台最高点A的仰角为22°,然后沿MP方向前进16m到达点N处,测得点A的仰角为45°.测角仪的高度为1.6m求观星台最高点A距离地面的高度(结果精确到0.1m.参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40, ≈1.41).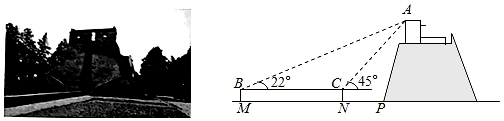 20. 如图,A,P,B,C是⊙O上的四点,∠APC=∠CPB=60°.
20. 如图,A,P,B,C是⊙O上的四点,∠APC=∠CPB=60°. (1)、判断△ABC的形状,并证明你的结论;(2)、求证:PA+PB=PC.21. 为落实关于开展中小学课后服务工作的要求,某学校开展了四门校本课程供学生选择:A.趣味数学;B.博乐阅读;C.快乐英语;D.硬笔书法.全校共有100名学生选择了A课程,为了解选A课程学生的学习情况,从这100名学生中随机抽取了30名学生进行测试.将他们的成绩(百分制)绘制成频数分布直方图.
(1)、判断△ABC的形状,并证明你的结论;(2)、求证:PA+PB=PC.21. 为落实关于开展中小学课后服务工作的要求,某学校开展了四门校本课程供学生选择:A.趣味数学;B.博乐阅读;C.快乐英语;D.硬笔书法.全校共有100名学生选择了A课程,为了解选A课程学生的学习情况,从这100名学生中随机抽取了30名学生进行测试.将他们的成绩(百分制)绘制成频数分布直方图. (1)、其中70≤x<80这一组的数据为74,73,72,75,76,76,79,则这组数据的中位数是 , 众数是 .(2)、根据题中信息,估计该校共有人,选A课程学生成绩在80≤x<90的有人.(3)、如果学校规定每名学生要选两门不同的课程,小张和小王在选课过程中,若第一次都选了课程C,那么他俩第二次同时选课程A或B的概率是多少?请用列表法或画树状图的方法加以说明.
(1)、其中70≤x<80这一组的数据为74,73,72,75,76,76,79,则这组数据的中位数是 , 众数是 .(2)、根据题中信息,估计该校共有人,选A课程学生成绩在80≤x<90的有人.(3)、如果学校规定每名学生要选两门不同的课程,小张和小王在选课过程中,若第一次都选了课程C,那么他俩第二次同时选课程A或B的概率是多少?请用列表法或画树状图的方法加以说明.

