安徽省合肥市蜀山区2022年九年级质量调研检测（一）数学试题

试卷更新日期：2022-05-30 类型：中考模拟

进入出卷网下载

一、单选题

1. 在-2， $\frac{1}{2}$ ， 0，-1这四个数中，最小的数是（）

A、-2 B、 $\frac{1}{2}$ C、0 D、-1

查看试题解析
2. 承载着复兴梦想的京张高铁，冬奥期间向世界展现“中国力量”和“中国自信”．京张高铁，总投资584亿元，584亿用科学记数法表示为（）.

A、5.84×10¹¹ B、584×10⁸ C、5.84×10¹⁰ D、0.584×10¹¹

查看试题解析
3. 下列立体图形中，主视图是三角形的是（）

A、 B、 C、 D、

查看试题解析
4. 计算 $a \cdot (- a^{2})^{3}$ 的结果是（）.

A、 $a^{6}$ B、 $- a^{6}$ C、 $a^{7}$ D、 $- a^{7}$

查看试题解析
5. 两个直角三角板ABC，ADE如图摆放，其中∠BAC=∠DEA = 90°，∠B=45°，∠D=60°，若DE $∥$ BC，则∠BAD的大小为（）

A、15° B、22.5° C、30° D、45°

查看试题解析
6. “稳字当头”的中国经济是全球经济的“稳定器”，稳就业，保民生，防风险，守住“稳”的基础，才有更多“进”的空间，2020、2021这两年中国经济的年平均增长率为5.1%，其中2021年的年增长率为8.1%，若设2020年的年增长率为x，则可列方程为（）

A、8.1%（1-x）²=5.1% B、（1+x）（1+8.1%）=（1+5.1%）² C、5.1%（1+x） = 8.1% D、（1+x）（1+8.1%）= 2（1+5.1%）

查看试题解析
7. 已知：a+b+c=0，a＜b＜c，若一次函数y=ax +c的图象经过点A，则点A的坐标不可以是（）

A、（-2，3） B、（-2，-3） C、（2，3） D、（2，-3）

查看试题解析
8. 甲乙两台机床同时生产同一种零件，在某周的工作日内，两台机床每天生产次品的个数整理成甲、乙两组数据，如下表：关于以上数据，下列说法正确的是（）
机床/星期
星期一
星期二
星期三
星期四
星期五
甲
2
0
4
3
2
乙
1
3
4
0
4

A、甲、乙的众数相同 B、甲、乙的中位数相同 C、甲的平均数大于乙的平均数 D、甲的方差小于乙的方差

查看试题解析
9. 如图，A、B表示足球门边框（不考虑球门的高度）的两个端点，点C表示射门点，连接AC、BC，则∠ACB就是射门角，在不考虑其它因素的情况下，一般射门角越大，射门进球的可能性就越大，球员甲带球线路ED与球门AB垂直，D为垂足，点C在ED上，当∠ACB最大时就是带球线路ED上的最佳射门角，若AB=4，BD=1，则当球员甲在此次带球中获得最佳射门角时DC的长度为（）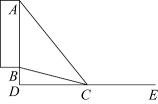

A、2 B、3 C、 $\sqrt{5}$ D、 $\sqrt{15}$

查看试题解析
10. 如图，在平面直角坐标系中，已知点A（-2，0）、B（-2，2）、C（0，2），当抛物线y=2（x-a）² +2a与四边形OABC的边有交点时a的取值范围是（）

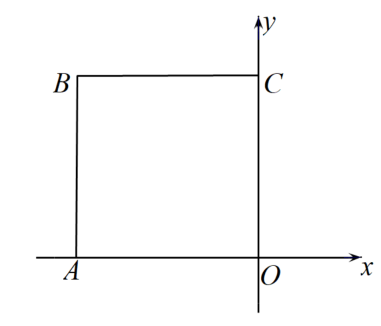A、-1≤a≤0 B、 $\frac{- 5 - \sqrt{13}}{2} \leq a \leq \frac{- 1 - \sqrt{5}}{2}$ C、 $- 4 \leq a \leq \frac{- 1 + \sqrt{5}}{2}$ D、 $\frac{- 5 - \sqrt{13}}{2} \leq a \leq \frac{- 1 + \sqrt{5}}{2}$

查看试题解析

二、填空题

11. 使 $\sqrt{x - 2}$ 有意义的x的取值范围是．

查看试题解析
12. 因式分解： $a b^{2} - a c^{2}$ =

查看试题解析
13. 如图，在平面直角坐标系中，点A的坐标为（4，0），点B在第一象限，且 $△$ OAB为等边三角形，若反比例函数y= $\frac{k}{x}$ 在第一象限的图象经过边AB的中点，则k的值为

查看试题解析
14. 已知：如图，△ABC中，BA= BC，∠ABC=70°，AC=4，点D是平面内动点，且AD=1，将BD绕点B顺时针旋转70°得到BE，连接AE．

(1)、在点D运动的过程中，AE的最小长度为；

(2)、在点D运动的过程中，当AE的长度最长时，则∠DAB=

查看试题解析

三、解答题

15. 计算： $202 2^{0} - (- 3)^{2} + \sqrt{18} \times \sqrt{2}$ ．

查看试题解析
16. 观察以下等式：第1个等式： $\frac{1}{3} \times (1 + \frac{2}{1}) = 3 - \frac{2}{1}$ ；第2个等式： $\frac{4}{4} \times (1 + \frac{2}{2}) = 3 - \frac{2}{2}$ ；第3个等式： $\frac{7}{5} \times (1 + \frac{2}{3}) = 3 - \frac{2}{3}$ ；第4个等式： $\frac{10}{6} \times (1 + \frac{2}{4}) = 3 - \frac{2}{4}$ ；……；按照以上规律，解决下列问题：

(1)、写出第5个等式：；

(2)、写出你猜想的第n个等式： ▲ （用含n的等式表示），并证明

查看试题解析
17. 如图，在每个小正方形的边长为1个单位的网格中，△ABC的顶点均在格点（网格线的交点）上
⑴画出△ABC关于y轴对称的△A₁B₁C₁（点A、B、C分别为A₁、B₁、C₁的对应点）
⑵将（1）中的△A₁B₁C₁绕原点O逆时针旋转90°得到△A₂B₂C₂ ，画出△A₂B₂C₂（点A₂、B₂、C₂分别为A₁、B₁、C₁的对应点）

查看试题解析
18. 如图，教学楼AB与旗杆CD的距离BC=12m，O在AB上，且OB= 1.5m，在某次数学活动课中，甲小组在A测得旗杆顶部D的俯角为30°，同时乙小组从0处测得旗杆顶部D的仰角为38.7°，求教学楼AB的高度（精确到0.1m），（参考数据：sin38.7°≈0.63，cos38.7≈0.78，tan38.7°=0.80， $\sqrt{3}$ =1.73）

查看试题解析
19. 如图，△ABC中，∠BAC＝45°，AC，BC交以AB为直径的半⊙O于D，E．连接AE，BD，交点为F．

(1)、证明：AF＝BC；

(2)、当点F是BD中点时，求BE：EC值．

查看试题解析
20. 一次函数y₁ =kx+b（k≠0）的图象与反比例函数y₂= $\frac{m}{x}$ （m≠0）的图象交于点A（-3，1）和点B （a，3）

(1)、求一次函数与反比例函数的解析式；

(2)、O为坐标原点，求点O到直线AB的距离；

查看试题解析
21. 教育部去年4月份发布《关于进一步加强中小学生睡眠管理工作的通知》，提出多项措施改善和保证学生睡眠时间，今年年初，某中学为了解九年级学生的睡眠状况，从九年级学生中随机抽取部分学生进行问卷调查，睡眠时间x时，分为A： x≥9；B：8≤x＜9，；C：7≤x＜8；D：x＜7四个睡眠时间段．请根据两幅统计图中的信息回答下列问题：

(1)、本次抽样调查共抽取了 ▲ 名学生，请补全条形统计图；

(2)、若该中学九年级共有1200名学生，请你估计该中学九年级学生中睡眠时间段为C的学生有多少名？

(3)、若从睡眠时间段为D的2名男生2名女生中随机的抽取2名学生，了解睡眠时间较少的原因，求所抽取的两人恰好都是女生的概率．

查看试题解析
22. 在平面直角坐标系xOy中，抛物线y=x²-2ax+a-2与x轴交点为A、B，

(1)、判断点（ $\frac{1}{2}$ ， - $\frac{7}{4}$ ）是否在抛物线y=x²-2ax+a-2上，并说明理由；

(2)、当线段AB长度为4时，求a的值；

(3)、若w= AB，w是否存在最值，若存在，请求出最值，若不存在，请说明由；

查看试题解析
23. 已知：如图1，△ABC中，∠CAB=120°， AC=AB，点D是BC上一点，其中∠ADC=α（30°＜α＜90°），将△ABD沿AD所在的直线折叠得到△AED，AE交CB于F，连接CE

(1)、求∠CDE与∠AEC的度数（用含α的代数式表示）；

(2)、如图2，当α=45°时，解决以下问题：
①已知AD=2，求CE的值；
②证明：DC-DE= $\sqrt{2}$ AD；

查看试题解析

机床/星期	星期一	星期二	星期三	星期四	星期五
甲	2	0	4	3	2
乙	1	3	4	0	4