安徽省合肥市肥西县2022年九年级第二次教学质量调研数学试卷
试卷更新日期:2022-05-30 类型:中考模拟
一、单选题
-
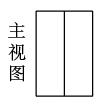
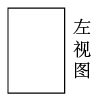
1. 在-2,-5,0,2这四个数中,最小的数是( )A、-2 B、-5 C、0 D、22. 下列运算正确的是( )A、 B、 C、 D、3. 某种细胞的直径是0.00000026m,将0.00000026用科学记数法表示为( )A、 B、 C、 D、4. 如图,是一个正三棱柱的三视图,则这个三棱柱摆放方式正确的是( )
 A、
A、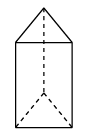 B、
B、 C、
C、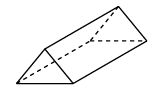 D、
D、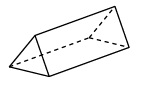 5. 如图,点A、B分别在直线a、b上,且直线a∥b,以点A为圆心,AB长为半径画弧交直线a于点C,连接BC,若∠2=65°,则∠1=( )
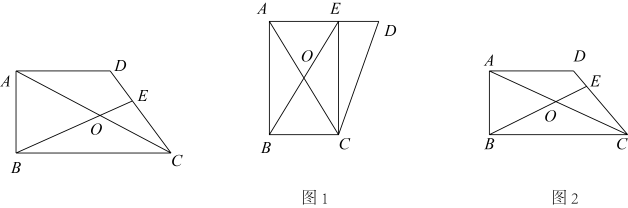
5. 如图,点A、B分别在直线a、b上,且直线a∥b,以点A为圆心,AB长为半径画弧交直线a于点C,连接BC,若∠2=65°,则∠1=( )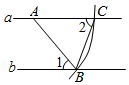 A、75° B、65° C、50° D、25°6. 不等式组的解集是( )A、x≥3 B、x≥﹣ C、﹣≤x≤3 D、无解7. 如图,矩形 ABCD 的对角线 AC 与 BD 相交于点 O,CE∥BD, DE∥AC , AD=2 , DE=2,则四边形 OCED 的面积为( )
A、75° B、65° C、50° D、25°6. 不等式组的解集是( )A、x≥3 B、x≥﹣ C、﹣≤x≤3 D、无解7. 如图,矩形 ABCD 的对角线 AC 与 BD 相交于点 O,CE∥BD, DE∥AC , AD=2 , DE=2,则四边形 OCED 的面积为( )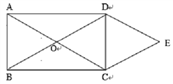 A、2 B、4 C、4 D、88. 已知三个实数a,b,c满足a+b﹣c=0,3a+b﹣c>0,则关于x的方程ax2﹣cx+b=0的根的情况是( )A、无实数根 B、有且只有一个实数根 C、两个实数根 D、无数个实数根9. 如图,在矩形ABCD中,AB=3,AD=2,点E是CD的中点,射线AE与BC的延长线相交于点F,点M从A出发,沿A→B→F的路线匀速运动到点F停止.过点M作MN⊥AF于点N.设AN的长为x,△AMN的面积为S,则能大致反映S与x之间函数关系的图象是( )
A、2 B、4 C、4 D、88. 已知三个实数a,b,c满足a+b﹣c=0,3a+b﹣c>0,则关于x的方程ax2﹣cx+b=0的根的情况是( )A、无实数根 B、有且只有一个实数根 C、两个实数根 D、无数个实数根9. 如图,在矩形ABCD中,AB=3,AD=2,点E是CD的中点,射线AE与BC的延长线相交于点F,点M从A出发,沿A→B→F的路线匀速运动到点F停止.过点M作MN⊥AF于点N.设AN的长为x,△AMN的面积为S,则能大致反映S与x之间函数关系的图象是( )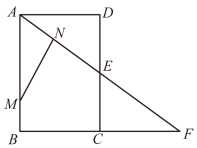 A、
A、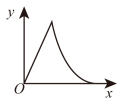 B、
B、 C、
C、 D、
D、 10. 如图,正比例函数y=2x与反比例函数的图象交于A、B两点,点P在以为圆心,1为半径的⊙C上运动,点Q是AP的中点,则OQ长的最大值为( )
10. 如图,正比例函数y=2x与反比例函数的图象交于A、B两点,点P在以为圆心,1为半径的⊙C上运动,点Q是AP的中点,则OQ长的最大值为( ) A、2 B、 C、 D、
A、2 B、 C、 D、二、填空题
-
11. 若式子 在实数范围内有意义,则x的取值范围是 .
12. 已知一组数据8,3,m,2的众数为3,则这组数据的平均数是.13. 设a、b是方程的两实数根,则 .14. 如图,在△ABC中,AB=4,点P为AC边上一点,PE⊥AB于点E,PF⊥BC于点F,将∠A、∠C分别沿PE、PF折叠,使点A、C分别落在边AB、BC上的点G、H处.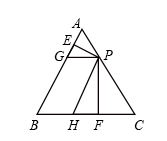 (1)、当∠B=50°时,则∠GPH= .(2)、当四边形BHPG为平行四边形时,则PE+PF的值为 .
(1)、当∠B=50°时,则∠GPH= .(2)、当四边形BHPG为平行四边形时,则PE+PF的值为 .三、解答题
-
15. 计算: .16. 如图,所示的正方形网格中,每个小正方形的边长均为1个单位,△ABC的三个顶点都在格点上,请按要求画图:
 (1)、在网格中画出△ABC向下平移5个单位得到的;(2)、在网格中画出关于直线l对称的;(3)、在网格中画出将△ABC绕点A按逆时针方向旋转90°得到的 .17. 阅读理解题:
(1)、在网格中画出△ABC向下平移5个单位得到的;(2)、在网格中画出关于直线l对称的;(3)、在网格中画出将△ABC绕点A按逆时针方向旋转90°得到的 .17. 阅读理解题:定义:如果一个数的平方等于-1,记为 , 这个数i叫做虚数单位,把形如a+bi(a,b为实数)的数叫做复数,其中a叫这个复数的实部,b叫做这个复数的虚部,它的加、减、乘法运算与整式的加、减、乘法运算类似.
例如计算:;
;
根据以上信息,完成下列问题:
(1)、填空: , ;(2)、计算:;(3)、计算: .18. 周末爬紫蓬山,是肥西县居民周末娱乐休闲、锻炼身体的方式之一.某个周末小华同学从紫蓬山东坡沿坡角为37°的山坡爬了150米,紧接着又爬了坡角为45°的山坡140米,最后到达山顶,请你计算紫蓬山的高度.(结果精确到个位,参考数据: , , , , . ) 19. 如图,双曲线经过点 , 且与直线有两个不同的交点.
19. 如图,双曲线经过点 , 且与直线有两个不同的交点.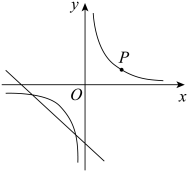 (1)、求m的值.(2)、求k的取值范围.20. 如图,在△ABC中,AB=AC,AD平分BC,BE平分∠ABC交AD于点E.点O在AB边上,以点O为圆心的⊙O经过B、E两点,交AB于点F.
(1)、求m的值.(2)、求k的取值范围.20. 如图,在△ABC中,AB=AC,AD平分BC,BE平分∠ABC交AD于点E.点O在AB边上,以点O为圆心的⊙O经过B、E两点,交AB于点F.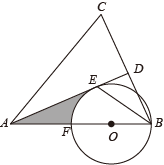 (1)、求证:AE是⊙O的切线;(2)、若∠BAC=60°,AC=12,求阴影部分的面积.21. 某学校为了解学生“第二课堂“活动的选修情况,对报名参加A.跆拳道,B.声乐,C.足球,D.古典舞这四项选修活动的学生(每人必选且只能选修一项)进行抽样调查.并根据收集的数据绘制了图①和图②两幅不完整的统计图.
(1)、求证:AE是⊙O的切线;(2)、若∠BAC=60°,AC=12,求阴影部分的面积.21. 某学校为了解学生“第二课堂“活动的选修情况,对报名参加A.跆拳道,B.声乐,C.足球,D.古典舞这四项选修活动的学生(每人必选且只能选修一项)进行抽样调查.并根据收集的数据绘制了图①和图②两幅不完整的统计图.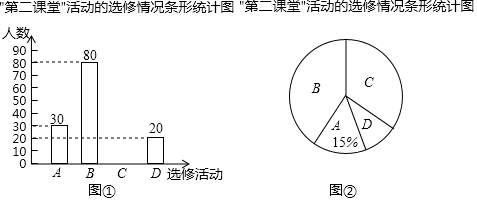
根据图中提供的信息,解答下列问题:
(1)、本次调查的学生共有人;在扇形统计图中,B所对应的扇形的圆心角的度数是;(2)、将条形统计图补充完整;(3)、在被调查选修古典舞的学生中有4名团员,其中有1名男生和3名女生,学校想从这4人中任选2人进行古典舞表演.请用列表或画树状图的方法求被选中的2人恰好是1男1女的概率.