安徽省蚌埠2022年中考二模数学试卷
试卷更新日期:2022-05-30 类型:中考模拟
一、单选题
-
1. 记4的算术平方根为 , 则的相反数是( )A、-4 B、-2 C、±2 D、±42. 下列运算正确的是( )A、 B、 C、 D、3. 蚌埠市统计局2022年1月28日《蚌埠市2021经济运行情况》指出:根据地区生产总值统一核算结果,2021年全市生产总值1989亿元.其中1989亿用科学记数法表示应为( )A、 B、 C、 D、4. 如图,已知某几何体的实物图和主(正)视图如图所示,则该几何体的左视图和俯视图是( )
 A、
A、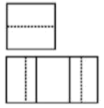 B、
B、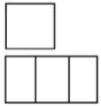 C、
C、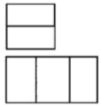 D、
D、 5. 若是不等式组的一个解,则的值可以是( )A、0 B、-2 C、3 D、-16. 如图,在中,点D,E,F,G分别是线段BC,AB,BD,AD的中点,设四边形EFDG的面积为 , 则的面积为( )
5. 若是不等式组的一个解,则的值可以是( )A、0 B、-2 C、3 D、-16. 如图,在中,点D,E,F,G分别是线段BC,AB,BD,AD的中点,设四边形EFDG的面积为 , 则的面积为( )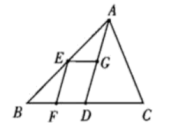 A、2S B、3S C、4S D、6S7. 已知关于的方程: , 则对这个方程的解的描述正确的是( )A、解为 B、解为 C、解为 D、无解8. 如图是温度计的示意图,图中左边的温度表示摄氏温度,右边的温度表示华氏温度.小明观察温度计发现,两个刻度x,y之间的关系如下表:
A、2S B、3S C、4S D、6S7. 已知关于的方程: , 则对这个方程的解的描述正确的是( )A、解为 B、解为 C、解为 D、无解8. 如图是温度计的示意图,图中左边的温度表示摄氏温度,右边的温度表示华氏温度.小明观察温度计发现,两个刻度x,y之间的关系如下表:x/℃
10
20
25
30
y/℉
50
68
77
86
据此可知,摄氏温度为15时,对应的华氏温度应为( )
 A、15 B、59 C、-9.4 D、549. 蚌埠市作为国家级“两区一点”城市,在智慧教育方面领先全国.据蚌埠市教育局微信公众号2022年3月20日发布的《2022年蚌埠市中小学智慧课堂教学抽样赛首次月汇总成绩公布》报道,今年2月25日—3月18日,市教育局每周五连续四周举行的蚌埠市初中语文、数学、英语、物理智慧课堂教学抽样赛成绩如表所示.若仅以表中数据为依据,则以下结论正确的是( )
A、15 B、59 C、-9.4 D、549. 蚌埠市作为国家级“两区一点”城市,在智慧教育方面领先全国.据蚌埠市教育局微信公众号2022年3月20日发布的《2022年蚌埠市中小学智慧课堂教学抽样赛首次月汇总成绩公布》报道,今年2月25日—3月18日,市教育局每周五连续四周举行的蚌埠市初中语文、数学、英语、物理智慧课堂教学抽样赛成绩如表所示.若仅以表中数据为依据,则以下结论正确的是( )县区
经开区
龙子湖区
蚌山区
禹会区
高新区
淮上区
局属
怀远县
固镇县
五河县
平均分
95.38
92.23
83.17
80.13
79.74
78.49
72.64
72.56
68.41
66.33
参赛教师数
1
2
3
3
3
3
3
2
3
1
A、这四次抽测所得数据的中位数一定满足 B、这四次抽测所得数据的平均数一定满足 C、这四次抽测所得数据的众数一定满足 D、这四次抽测所得数据的最大数与最小数的差一定是29.0510. 已知矩形MNPQ的顶点M,N,P,Q分别在正六边形ABCDEF的边DE,FA,AB,CD上,且 . 在点从移向(与不重合)的过程中,下列的判断中,正确的是( )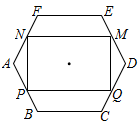 A、矩形MNPQ的面积与周长保持不变 B、矩形MNPQ的面积逐渐减小,周长逐渐增大 C、矩形MNPQ的面积与周长均逐渐增大 D、矩形MNPQ的面积与周长均逐渐减小
A、矩形MNPQ的面积与周长保持不变 B、矩形MNPQ的面积逐渐减小,周长逐渐增大 C、矩形MNPQ的面积与周长均逐渐增大 D、矩形MNPQ的面积与周长均逐渐减小二、填空题
-
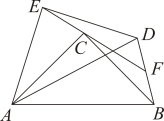
11. 因式分解: .12. 如图,中, , M是BC的中点,的内切圆与AB,BM分别相切于点D,E,连接DE.若 , 则的大小为 .
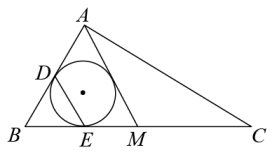 13. 在一个不透明的袋子里有1个红球,2个白球和若干个黑球.小宇将袋子中的球摇匀后,从中任意摸出一个,记下颜色后放回袋中,在多次重复以上操作后,小宇统计了摸到红球的频率,并绘制了如图折线图.则从袋子中随机摸出两个球,这两个球一红一白的概率为 .
13. 在一个不透明的袋子里有1个红球,2个白球和若干个黑球.小宇将袋子中的球摇匀后,从中任意摸出一个,记下颜色后放回袋中,在多次重复以上操作后,小宇统计了摸到红球的频率,并绘制了如图折线图.则从袋子中随机摸出两个球,这两个球一红一白的概率为 .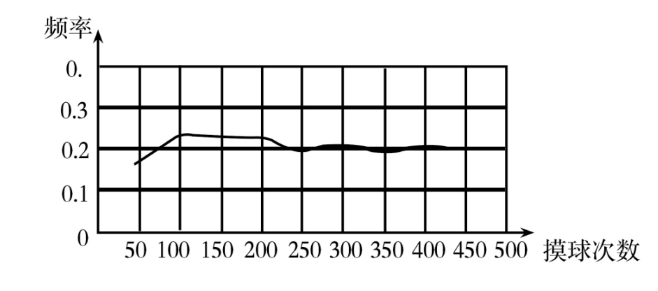
三、解答题
-
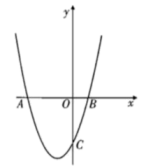
14. 如图,正方形的顶点 , 分别在 , 轴的正半轴上,对角线 , 的交点在第一象限,反比例函数的图象经过点,已知轴.
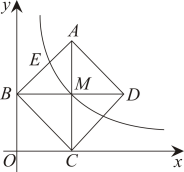 (1)、若正方形面积为4,则的值为;(2)、若反比例函数的图象与交于点 , 则 .15. 计算: .16. 新能源汽车节能、环保,越来越受消费者喜爱.2020年某款新能源汽车销售量为15万辆,销售量逐年增加,2022年预估当年销售量为21.6万辆,求这款新能源汽车的年平均增长率.17. 如图,在由边长为1个单位长度的小正方形组成的网格中,给出了以格点(网格线的交点)为顶点的△ABC,△DEF,已知点M,N都是格点.
(1)、若正方形面积为4,则的值为;(2)、若反比例函数的图象与交于点 , 则 .15. 计算: .16. 新能源汽车节能、环保,越来越受消费者喜爱.2020年某款新能源汽车销售量为15万辆,销售量逐年增加,2022年预估当年销售量为21.6万辆,求这款新能源汽车的年平均增长率.17. 如图,在由边长为1个单位长度的小正方形组成的网格中,给出了以格点(网格线的交点)为顶点的△ABC,△DEF,已知点M,N都是格点.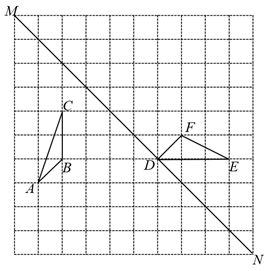 (1)、作出△ABC关于直线MN对称的;(2)、将向上平移4个单位长度得到新的三角形,请画出该三角形;(3)、填空:(直接写出结果).18. 某市初中数学进行了学生在线测试,从全体参与测试的300名学生中随机选取了20名学生的在线考试成绩(满分100分,成绩取整数),将这20名学生的成绩按从低到高的顺序整理成表1,并划分为四个等级,划分标准如表2.已知这些成绩的众数是唯一的,且中位数是79.5.
(1)、作出△ABC关于直线MN对称的;(2)、将向上平移4个单位长度得到新的三角形,请画出该三角形;(3)、填空:(直接写出结果).18. 某市初中数学进行了学生在线测试,从全体参与测试的300名学生中随机选取了20名学生的在线考试成绩(满分100分,成绩取整数),将这20名学生的成绩按从低到高的顺序整理成表1,并划分为四个等级,划分标准如表2.已知这些成绩的众数是唯一的,且中位数是79.5.表1
学生编号
①
②
③
④
⑤
⑥
⑦
⑧
⑨
⑩
成绩(x分)
40
56
57
57
62
68
73
75
75
79
学生编号
⑪
⑫
⑬
⑭
⑮
⑯
⑰
⑱
⑲
⑳
成绩(x分)
a
80
85
86
86
b
93
96
96
100
表2
成绩范围
不及格
x<60
不及格
及格
良好
优秀
注:在统计良好人数时,将优秀计算在内;在统计及格人数时,将良好(含优秀)计算在内.
(1)、 , ;(2)、据此估计全市300名学生中优秀的人数.19. 观察以下等式:第1个等式:;
第2个等式:;
第3个等式:;
第4个等式:;
第5个等式:
……
按照以上规律,解决下列问题:
(1)、第6个等式是;(2)、写出你猜想的第个等式: ▲ (用含的等式表示),并证明.20. 如图,AB是圆的直径,C,D是圆上的点(在AB同侧),过点D的圆的切线交直线AB于点 .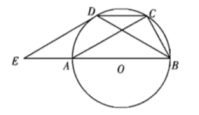 (1)、若 , , 求AC的长;(2)、若四边形ACDE是平行四边形,证明:BD平分 .21. 某校初中数学综合实践开展了多彩的活动.在一次活动中,某兴趣小组学习了以下史料:魏晋时刘徽撰写的《海岛算经》是有关测量的数学著作,其中第一题是测海岛的高:如图,点 , H,G在水平线AC上,DE和FG是两个垂直于水平面且等高的测量标杆的高度,称为“表高”,EG称为“表距”,GC和EH都称为“表目距”,GC与EH的差称为“表目距的差”,则海岛的高 .
(1)、若 , , 求AC的长;(2)、若四边形ACDE是平行四边形,证明:BD平分 .21. 某校初中数学综合实践开展了多彩的活动.在一次活动中,某兴趣小组学习了以下史料:魏晋时刘徽撰写的《海岛算经》是有关测量的数学著作,其中第一题是测海岛的高:如图,点 , H,G在水平线AC上,DE和FG是两个垂直于水平面且等高的测量标杆的高度,称为“表高”,EG称为“表距”,GC和EH都称为“表目距”,GC与EH的差称为“表目距的差”,则海岛的高 . (1)、该兴趣小组学过解直角三角形后,对该问题的测量方法进行了改良:测得两次测量点之间的距离 , 且 , , 请求出海岛的高AB(其中).(结果保留两位小数,参考数据: , )(2)、证明:海岛的高 .
(1)、该兴趣小组学过解直角三角形后,对该问题的测量方法进行了改良:测得两次测量点之间的距离 , 且 , , 请求出海岛的高AB(其中).(结果保留两位小数,参考数据: , )(2)、证明:海岛的高 .