广东省汕头市潮阳区2022年5月初中学业水平模拟考试数学试题
试卷更新日期:2022-05-30 类型:中考模拟
一、单选题
-
1. 下列四个数中,最小的是( )A、0 B、-4 C、 D、2. 据专家预测,到2022年冬残奥会结束时,冬奥会场馆预计共消耗绿电4亿度,预计可减少标煤燃烧12.8万吨,减排二氧化碳32万吨,将“32万”用科学记数法表示为( )A、32×104 B、3.2×105 C、3.2×104 D、0.32×1063. 以下是清华大学、北京大学、上海交通大学、浙江大学的校徽,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列运算正确的是( )A、3a+2b=5ab B、 C、(ab)2=a2b2 D、5. 下面四个几何体中,俯视图为四边形的是( )A、
4. 下列运算正确的是( )A、3a+2b=5ab B、 C、(ab)2=a2b2 D、5. 下面四个几何体中,俯视图为四边形的是( )A、 B、
B、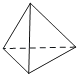 C、
C、 D、
D、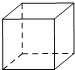 6. 近年来,我国持续大面积的雾霾天气让环保和健康问题成为焦点.为进一步普及环保和健康知识,我市某校举行了“建设宜居成都,关注环境保护”的知识竞赛,某班的学生成绩统计如下:
6. 近年来,我国持续大面积的雾霾天气让环保和健康问题成为焦点.为进一步普及环保和健康知识,我市某校举行了“建设宜居成都,关注环境保护”的知识竞赛,某班的学生成绩统计如下:成绩(分)
60
70
80
90
100
人 数
4
8
12
11
5
则该办学生成绩的众数和中位数分别是( )
A、70分,80分 B、80分,80分 C、90分,80分 D、80分,90分7. 在某核酸检测任务中,甲医疗队比乙医疗队每小时多检测15人,甲队检测600人所用的时间比乙队检测500人所用的时间少 . 设甲队每小时检测人,根据题意,可列方程为A、 B、 C、 D、8. 如图,⊙O中,半径OC⊥弦AB于点D,点E在⊙O上,∠E=22.5°,AB=6,则半径OB等于( )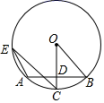 A、 B、3 C、 D、69. 在同一坐标系中,函数y=和y=﹣kx+3的大致图象可能是( )A、
A、 B、3 C、 D、69. 在同一坐标系中,函数y=和y=﹣kx+3的大致图象可能是( )A、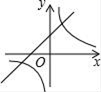 B、
B、 C、
C、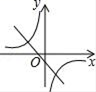 D、
D、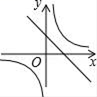 10. 勾股定理是人类早期发现并证明的重要数学定理之一,是数形结合的重要纽带.数学家欧几里得利用如图验证了勾股定理:以直角三角形的三条边为边长向外作正方形 , 正方形 , 正方形 , 连接 , , 过点作于点 , 交于点 . 设正方形的面积为 , 正方形的面积为 , 长方形的面积为 , 长方形的面积为 , 下列结论:①;②;③;④ . 其中正确的结论有( )
10. 勾股定理是人类早期发现并证明的重要数学定理之一,是数形结合的重要纽带.数学家欧几里得利用如图验证了勾股定理:以直角三角形的三条边为边长向外作正方形 , 正方形 , 正方形 , 连接 , , 过点作于点 , 交于点 . 设正方形的面积为 , 正方形的面积为 , 长方形的面积为 , 长方形的面积为 , 下列结论:①;②;③;④ . 其中正确的结论有( )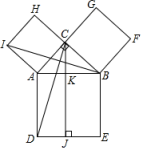 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
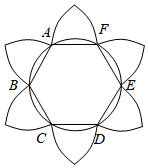
11. 代数式 有意义,则x的取值范围是 .12. 如图,花瓣图案中的正六边形ABCDEF的每个内角的度数是.
 13. 已知一个二次函数的二次项的系数是1,且经过点(1,0),请写一个符合上述条件的二次函数表达式 .14. 不等式组的解集是 .15. 如图,从甲楼底部A处测得乙楼顶部C处的仰角是30°,从甲楼顶部B处测得乙楼底部D处的俯角是45°,已知甲楼的高AB是60m,则乙楼的高CD是m(结果保留根号)
13. 已知一个二次函数的二次项的系数是1,且经过点(1,0),请写一个符合上述条件的二次函数表达式 .14. 不等式组的解集是 .15. 如图,从甲楼底部A处测得乙楼顶部C处的仰角是30°,从甲楼顶部B处测得乙楼底部D处的俯角是45°,已知甲楼的高AB是60m,则乙楼的高CD是m(结果保留根号)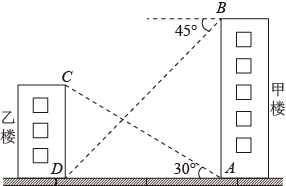 16. 如图,过反比例函数(x>0)图象上一点A作x轴的平行线,交双曲线(x<0)于点B,过B作BCOA交双曲线y(x<0)于点D,交x轴于点C,连接AD交y轴于点E.若OC=3,则△AOE的面积是 .
16. 如图,过反比例函数(x>0)图象上一点A作x轴的平行线,交双曲线(x<0)于点B,过B作BCOA交双曲线y(x<0)于点D,交x轴于点C,连接AD交y轴于点E.若OC=3,则△AOE的面积是 .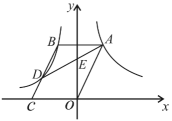 17. 如图,在△ABC中,∠C=90°,AC=8,AB=10,D是AC上一点,且CD=3,E是BC边上一点,将△DCE沿DE折叠,使点C落在点F处,连接BF,则BF的最小值为 .
17. 如图,在△ABC中,∠C=90°,AC=8,AB=10,D是AC上一点,且CD=3,E是BC边上一点,将△DCE沿DE折叠,使点C落在点F处,连接BF,则BF的最小值为 .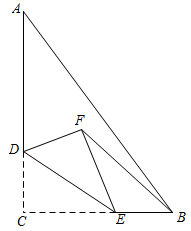
三、解答题
-
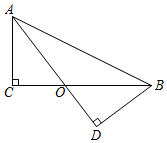
18. 已知=2是关于的一元二次方程2(2m+3)+m2+3m+2=0的一个根,求m的值.19. 先化简、再求值: , 其中20. 如图,在Rt△ACB和Rt△ADB中,∠C=∠D=90°,AD=BC,AD、BC相交于点O.
求证:CO=DO.
 21. 为了贯彻“减负增效”精神,掌握九年级学生每天的自主学习情况,某校学生会随机抽查了九年级的部分学生,并调查他们每天自主学习的时间.根据调查结果,制作了两幅不完整的统计图(图1,图2),请根据统计图中的信息回答下列问题:
21. 为了贯彻“减负增效”精神,掌握九年级学生每天的自主学习情况,某校学生会随机抽查了九年级的部分学生,并调查他们每天自主学习的时间.根据调查结果,制作了两幅不完整的统计图(图1,图2),请根据统计图中的信息回答下列问题: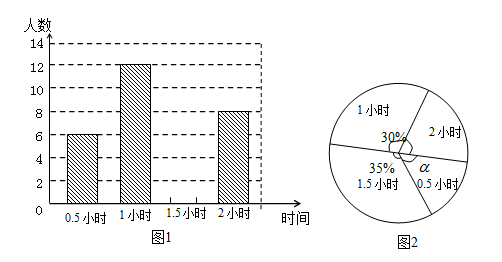 (1)、本次调查的学生人数是人;(2)、图2中a是 ▲ 度,并将图1条形统计图补充完整;(3)、老师从自主学习效果较好的4位同学(分别记为A、B、C、D)随机选择两位进行学习经验交流,请用列表法或树状图的方法求出同时选中A,B两位同学的概率.22. 在“抗击疫情”期间,某学校工会号召广大教师积极开展了“献爱心捐款”活动,学校拟用这笔捐款购买A、B两种防疫物品.如果购买A种物品30件,B种物品20件,共需680元;如果购买A种物品50件,B种物品40件,共需1240元.(1)、求A、B两种防疫物品每件各多少元;(2)、现要购买A、B两种防疫物品共300件,总费用不超过4000元,那么A种防疫物品最多购买多少件?23. 如图,AB是⊙O的直径,点E为线段OB上一点(不与O,B重合),作CE⊥OB,交⊙O于点C,垂足为点E,作直径CD,过点C的切线交DB的延长线于点P,作AF⊥PC于点F,连接CB.
(1)、本次调查的学生人数是人;(2)、图2中a是 ▲ 度,并将图1条形统计图补充完整;(3)、老师从自主学习效果较好的4位同学(分别记为A、B、C、D)随机选择两位进行学习经验交流,请用列表法或树状图的方法求出同时选中A,B两位同学的概率.22. 在“抗击疫情”期间,某学校工会号召广大教师积极开展了“献爱心捐款”活动,学校拟用这笔捐款购买A、B两种防疫物品.如果购买A种物品30件,B种物品20件,共需680元;如果购买A种物品50件,B种物品40件,共需1240元.(1)、求A、B两种防疫物品每件各多少元;(2)、现要购买A、B两种防疫物品共300件,总费用不超过4000元,那么A种防疫物品最多购买多少件?23. 如图,AB是⊙O的直径,点E为线段OB上一点(不与O,B重合),作CE⊥OB,交⊙O于点C,垂足为点E,作直径CD,过点C的切线交DB的延长线于点P,作AF⊥PC于点F,连接CB.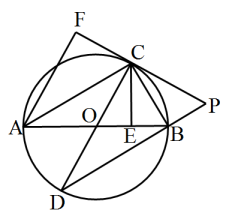 (1)、求证:△CBE∽△CPB;(2)、当且时,求扇形COB的面积.24. 如图
(1)、求证:△CBE∽△CPB;(2)、当且时,求扇形COB的面积.24. 如图 (1)、模型建立,如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于D,过B作BE⊥ED于E.求证:△BEC≌△CDA;(2)、模型应用:
(1)、模型建立,如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于D,过B作BE⊥ED于E.求证:△BEC≌△CDA;(2)、模型应用:①已知直线AB与y轴交于A点,与轴交于B点,sin∠ABO= , OB=4,将线段AB绕点B逆时针旋转90度,得到线段BC,过点A,C作直线,求直线AC的解析式;
②如图3,矩形ABCO,O为坐标原点,B的坐标为(8,6),A,C分别在坐标轴上,P是线段BC上动点,已知点D在第一象限,且是直线y=25上的一点,若△APD是以D为直角顶点的等腰直角三角形,请求出所有符合条件的点D的坐标.
25. 抛物线 经过点 和点 ,与 轴交于点 .(1)、求该抛物线的函数表达式;(2)、点 是该抛物线上的动点,且位于 轴的左侧.①如图1,过点 作 轴于点 ,作 轴于点 ,当 时,求 的长;

②如图2,该抛物线上是否存在点 ,使得 ?若存在,请求出所有点 的坐标;若不存在,请说明理由.
