云南省昭通市昭阳区2022年初中学业水平模拟监测数学试卷（一）

试卷更新日期：2022-05-30 类型：中考模拟

进入出卷网下载

一、单选题

1. 一个数的相反数是 $- \frac{1}{6}$ ，则这个数是（）

A、 $\frac{1}{6}$ B、 $- \frac{1}{6}$ C、6 D、 $- 6$

查看试题解析
2. 直线a//b，其中∠1＝20°， ∠2＝36°，∠3为（）

A、56° B、124° C、34° D、36°

查看试题解析
3. 下列图形中，是中心对称图形的是( )

A、 B、 C、 D、

查看试题解析
4. 下列计算正确的是（）

A、 ${(- 2 a^{2} b)}^{3} = - 8 a^{6} b^{3}$ B、 $a^{6} \div a^{3} = a^{2}$ C、 $2 a + 3 b = 5 a b$ D、 $a^{0} = 1$

查看试题解析
5. 已知一个多边形的每一个内角都比它相邻的外角的4倍多30°，这个多边形是（）

A、十边形 B、十一边形 C、十二边形 D、十三边形

查看试题解析
6. 使二次根式 $\frac{\sqrt{x - 2}}{3}$ 有意义的 $x$ 的取值范围是（）

A、 $x \neq 2$ B、 $x \neq 3$ C、 $x > 3$ D、 $x \geq 2$

查看试题解析
7. 如图，已知△ADE和△ABC的相似比是1：2，且△ADE的面积为2，则四边形DBCE的面积是（）

A、8 B、6 C、4 D、2

查看试题解析
8. 若关于 $x$ 的一元二次方程 $(1 - m) x^{2} + 2 x - 7 = 0$ 有两个不相等的实数根，则 $m$ 的取值范围是（）

A、 $m \leq \frac{8}{7}$ B、 $m \leq \frac{8}{7}$ 且 $m \neq 1$ C、 $m > \frac{8}{7}$ D、 $m < \frac{8}{7}$ 且 $m \neq 1$

查看试题解析
9. 按一定规律排列的单项式： $- x^{3}$ ， $x^{5}$ ， $- x^{7}$ ， $x^{9}$ ， $- x^{11}$ ， ……，第n个单项式是（）

A、 ${(- 1)}^{n - 1} x^{2 n - 1}$ B、 ${(- 1)}^{n} x^{2 n - 1}$ C、 ${(- 1)}^{n - 1} x^{2 n + 1}$ D、 ${(- 1)}^{n} x^{2 n + 1}$

查看试题解析
10. 一个几何体的三视图如图所示，则这个几何体的侧面积是（）

A、 $27 π {cm}^{2}$ B、 $48 π {cm}^{2}$ C、 $96 π {cm}^{2}$ D、 $36 π {cm}^{2}$

查看试题解析
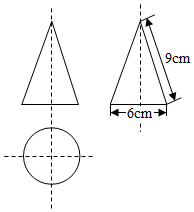11. 某优秀毕业生向我校赠送1080本课外书，现用A、B两种不同型号的纸箱包装运送，单独使用B型纸箱比单独使用A型纸箱可少用6个；已知每个B型纸箱比每个A型纸箱可多装15本．若设每个A型纸箱可以装书x本，则根据题意列得方程为（）

A、 $\frac{1080}{x} = \frac{1080}{x - 15} + 6$ B、 $\frac{1080}{x} = \frac{1080}{x - 15} - 6$ C、 $\frac{1080}{x + 15} = \frac{1080}{x} - 6$ D、 $\frac{1080}{x + 15} = \frac{1080}{x} + 6$

查看试题解析
12. 已知关于x的不等式组 ${\begin{array}{l} x - a \geq 0 \\ 3 - 2 x > 0 \end{array}$ 的整数解共有4个，则a的取值范围是（）

A、 $- 3 \leq a < - 2$ B、 $- 3 < a \leq - 2$ C、 $- 3 < a < - 2$ D、 $a < - 2$

查看试题解析

二、填空题

13. 已知实数a、b，满足 ${(a + 2)}^{2} + \sqrt{b - 3} = 0$ ，则ab的值．

查看试题解析
14. 把多项式x³﹣16xy²分解因式的结果是．

查看试题解析
15. 已知点 $A (a ， 1)$ ， $B (- 4 ， b)$ 在同一个反比例函数的图象上，则 $\frac{a}{b}$ 的值为．

查看试题解析
16. 如图， $R t △ A B C$ 中， $∠ C = 90 °$ ， $A C = 2 B C$ ，则 $c o s B$ 的值为．

查看试题解析
17. 如图，在 $△ A B C$ 中，DE是AC的垂直平分线， $A E = 3 c m$ ， $△ A B C$ 的周长为19cm，则 $△ A B D$ 的周长为．

查看试题解析
18. 在 $▱ A B C D$ 中， $∠ A = 45 °$ ， $A D = 6 \sqrt{2}$ ， $B D = 2 \sqrt{10}$ ，则 $▱ A B C D$ 的面积等于．

查看试题解析

三、解答题

19. 想了解某次数学测验的成绩情况，抽样调查了九年级（7）班的成绩，分别记作60分、70分、80分、90分、100分，并将统计结果绘制成不完整的统计图（如图）．

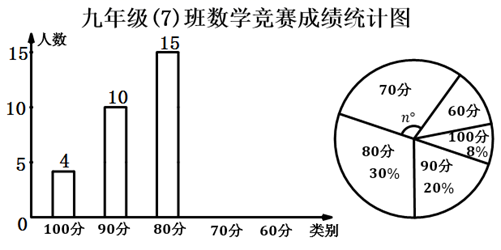(1)、样本容量为，成绩的中位数为；

(2)、若成绩为60分的人数为6人，则 $n$ = ．

(3)、若全校有1500人，估计全校90分及以上的同学大约多少人？

查看试题解析
20. “一方有难，八方支援”．武汉新冠病毒牵动着全国人民的心，我市某医院甲、乙、丙三位医生和 $A$ 、 $B$ 两名护士报名支援武汉．

(1)、若从甲、乙、丙三位医生中随机选一位医生，求恰好选中医生甲的概率；

(2)、若从甲、乙、丙三位医生和 $A$ 、 $B$ 两名护士中随机选一位医生和一名护士，求恰好选中医生甲和护士 $A$ 的概率．

查看试题解析
21. 如图，在四边形ABCD中，∠ACB＝90°， $A B ∥ C D$ ，点E是AB的中点，连接EC，过点E作EF⊥AD，垂足为F，已知 $A D ∥ E C$ ．

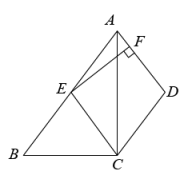(1)、求证：四边形AECD是菱形：

(2)、若AB＝25，BC＝15，求线段EF的长

查看试题解析
22. 某市雾霾天气趋于严重，甲商场根据民众健康需要，代理销售每台进价分别为600元、560
元的 A、B 两种型号的空气净化器，如表是近两周的销售情况：（进价、售价均保持不变，利润=销
售收入−进货成本）
销售时段
销售数量
销售收入（元）
A种型号
（台）
B种型号
（台）
第一周
3
2
3960
第二周
5
4
7120

(1)、求 A，B 两种型号的空气净化器的销售单价；

(2)、该商店计划一次购进两种型号的空气净化器共30台，其中B型净化器的进货量不超过A型的2倍．设购进A型空气净化器为x台，这30台空气净化器的销售总利润为y元．
①请写出y关于x的函数关系式；
②该商店购进A型、B型净化器各多少台，才能使销售总利润最大？

查看试题解析
23. 如图，在 $R t △ A B C$ 中， $∠ A B C = 90 °$ ，以AB为直径的 $⊙ O$ 交AC于点D，E是BC的中点，连接DE，BD．

(1)、求证：DE是 $⊙ O$ 的切线；

(2)、若 $D E = 4$ ， $s i n C = \frac{3}{5}$ ，求BD的长．

查看试题解析
24. 如图，抛物线y＝ax²+bx+4（a≠0）与x轴交于点A（﹣1，0）和点B（4，0），与y轴交于点C，顶点为D，连接AC，BC，BC与抛物线的对称轴l交于点E.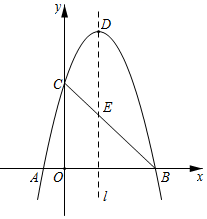

(1)、求抛物线的表达式；

(2)、点P是第一象限内抛物线上的动点，连接PB，PC，若S_△PBC＝ $\frac{3}{5}$ S_△ABC ，求点P的坐标；

(3)、点N是对称轴l右侧抛物线上的动点，在射线ED上是否存在点M，使得以点M，N，E为顶点的三角形与△OBC相似？若存在，直接写出点M的坐标；若不存在，说明理由.

查看试题解析

销售时段	销售数量		销售收入（元）
销售时段	A种型号（台）	B种型号（台）	销售收入（元）
第一周	3	2	3960
第二周	5	4	7120