云南省双柏县2022年初中学业水平考试数学模拟试题(一)
试卷更新日期:2022-05-30 类型:中考模拟
一、单选题
-
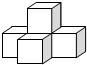
1. 数轴上比-5小4的数是( )A、-1 B、-9 C、1 D、-42. 第七次全国人口普查结果显示,我国具有大学文化程度的人口超218000000人.数据218000000用科学记数法表示为( )A、 B、 C、 D、3. 下图是五个相同的小正方体搭成的几何体,其左视图是( )
 A、
A、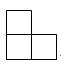 B、
B、 C、
C、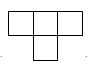 D、
D、 4. 下列计算正确的是( )A、(a-1)2=a2-1 B、4a·2a=8a2 C、2a-a=2 D、a8÷a2=a45. 一个圆锥的底面半径是2,母线长是4,则这个圆锥的表面积为( )A、4π B、20π C、8π D、12π6. 观察下列式子:
4. 下列计算正确的是( )A、(a-1)2=a2-1 B、4a·2a=8a2 C、2a-a=2 D、a8÷a2=a45. 一个圆锥的底面半径是2,母线长是4,则这个圆锥的表面积为( )A、4π B、20π C、8π D、12π6. 观察下列式子:第1个式子:2×4+1=9=32;
第2个式子:6×8+1=49=72;
第3个式子:14×16+1=225=152;
…………
则第n个式子的值为( )
A、(2n+1-1)2 B、(2n-1)2 C、(n3-1)2 D、(3n)27. 下列图形既是轴对称图形,又是中心对称图形的是( )A、平行四边形 B、三角形 C、等腰三角形 D、矩形8. 如图,△ABC内接于⊙O,∠CAB=30°,∠CBA=45°,CD⊥AB于点D,若⊙O的半径为2,则CD的长为( ) A、1 B、2 C、 D、9. 垃圾分类收集可以减少垃圾处理量,降低处理成本,减少土地资源的消耗,具有社会、经济、生态三方面的效益.某校从全校1400名学生中随机抽取了部分学生进行“垃圾分类及投放知识”测试,把测试成绩分为“优、良、中、差”四个等级,并进行统计,绘制了下面两幅统计图,下列说法中错误的是( )
A、1 B、2 C、 D、9. 垃圾分类收集可以减少垃圾处理量,降低处理成本,减少土地资源的消耗,具有社会、经济、生态三方面的效益.某校从全校1400名学生中随机抽取了部分学生进行“垃圾分类及投放知识”测试,把测试成绩分为“优、良、中、差”四个等级,并进行统计,绘制了下面两幅统计图,下列说法中错误的是( ) A、共抽取的学生人数为42人 B、α=120° C、全校得到“差”等级的人数约有200人 D、得到“优”和“良”等级人数之和占抽取总人数的百分比超过了72%10. 已知一元二次方程x2+mx+m=0有两个相等的实数根,则m的值为( )A、m=0 B、m=4 C、m=0,或m=4 D、m=0,或m=-411. 已知 为锐角,且 ,则 ( )A、 B、 C、 D、12. 若整数a既使得关于x的分式方程 有整数解,又使得关于x,y的方程组 的解为正数,则符合条件的所有a的个数为( )A、1 B、2 C、3 D、4
A、共抽取的学生人数为42人 B、α=120° C、全校得到“差”等级的人数约有200人 D、得到“优”和“良”等级人数之和占抽取总人数的百分比超过了72%10. 已知一元二次方程x2+mx+m=0有两个相等的实数根,则m的值为( )A、m=0 B、m=4 C、m=0,或m=4 D、m=0,或m=-411. 已知 为锐角,且 ,则 ( )A、 B、 C、 D、12. 若整数a既使得关于x的分式方程 有整数解,又使得关于x,y的方程组 的解为正数,则符合条件的所有a的个数为( )A、1 B、2 C、3 D、4二、填空题
-
13. 如图,直线c与直线a、b都相交.若 , ∠1=126°,则∠2=度.
 14. 不等式组的解集是 .15. 已知反比例函数(k≠0)与正比例函数y=2x的图象交于点P(1,-m).则反比例函数的表达式为 .16. 若一个正多边形的每一个外角都是30°,则这个正多边形的内角和等于度.17. 计算:= .18. 已知平行四边形ABCD中,AB=5,∠ABC与∠DCB的平分线分别交AD边于点E、F,且EF=3,则边AD的长为 .
14. 不等式组的解集是 .15. 已知反比例函数(k≠0)与正比例函数y=2x的图象交于点P(1,-m).则反比例函数的表达式为 .16. 若一个正多边形的每一个外角都是30°,则这个正多边形的内角和等于度.17. 计算:= .18. 已知平行四边形ABCD中,AB=5,∠ABC与∠DCB的平分线分别交AD边于点E、F,且EF=3,则边AD的长为 .三、解答题
-
19. 某校将学生体质健康测试成绩分为A,B,C,D四个等级,依次记为4分,3分,2分,1分.为了解学生整体体质健康状况,拟抽样进行统计分析.
 (1)、以下是两位同学关于抽样方案的对话:
(1)、以下是两位同学关于抽样方案的对话:小红:“我想随机抽取七年级男、女生各60人的成绩.”
小明:“我想随机抽取七、八、九年级男生各40人的成绩.”
根据如图学校信息,请你简要评价小红、小明的抽样方案.
如果你来抽取120名学生的测试成绩,请给出抽样方案.
(2)、现将随机抽取的测试成绩整理并绘制成如图统计图,请求出这组数据的平均数、中位数和众数.20. 联合国《生物多样性公约》第十五次缔约大会于2021年10月在昆明举行,为选出该会议的宣传大使,某区组织了七年级、八年级的学生参加宣讲比赛,主题为:“生态文明:共建地球生命共同体”.该区某校经过初选,在七年级中选出1男1女两名同学,分别记为A1 , B1;在八年级中选出3名同学,其中2名男生分别记为A2 , A3 , 1名女生记为B2 , 现分别从两个年级初选出的同学中,每个年级随机选出一名同学组成代表队参加宣讲比赛.(1)、用列表法或树状图法(树状图也称树形图),求出所有可能出现的结果;(2)、现从这5名同学中随机选出两名同学,求选中两名男生且他们来自不同年级的概率.21. 如图,AB为⊙O的直径,C为⊙O上一点,连接AC,BC,CD平分∠ACB与⊙O交于另一点D,过点D的直线EF平行于BA,E,F分别是CB,CA与直线EF的交点. (1)、求证:EF是⊙O的切线;(2)、若AC=3,BC= , 求BE的长.22. 甲超市在端午节这天进行苹果优惠促销活动,苹果的标价为10元 ,如果一次购买 以上的苹果,超过 的部分按标价6折售卖. (单位: )表示购买苹果的重量, (单位:元)表示付款金额.(1)、文文购买 苹果需付款元,购买 苹果需付款元;(2)、求付款金额 关于购买苹果的重量 的函数解析式;(3)、当天,隔壁的乙超市也在进行苹果优惠促销活动,同样的苹果的标价也为10元 ,且全部按标价的8折售卖.文文如果要购买 苹果,请问她在哪个超市购买更划算?
(1)、求证:EF是⊙O的切线;(2)、若AC=3,BC= , 求BE的长.22. 甲超市在端午节这天进行苹果优惠促销活动,苹果的标价为10元 ,如果一次购买 以上的苹果,超过 的部分按标价6折售卖. (单位: )表示购买苹果的重量, (单位:元)表示付款金额.(1)、文文购买 苹果需付款元,购买 苹果需付款元;(2)、求付款金额 关于购买苹果的重量 的函数解析式;(3)、当天,隔壁的乙超市也在进行苹果优惠促销活动,同样的苹果的标价也为10元 ,且全部按标价的8折售卖.文文如果要购买 苹果,请问她在哪个超市购买更划算?


