云南省临沧市耿马县2022年九年级学业水平考试（二模）数学试题

试卷更新日期：2022-05-30 类型：中考模拟

进入出卷网下载

一、单选题

1. ﹣2022的绝对值是（）

A、2022 B、 $\frac{1}{2}$ C、﹣2022 D、 $- \frac{1}{2}$

查看试题解析
2. 如图是由5个相同的正方体堆成的组合体，它的俯视图是（）

A、 B、 C、 D、

查看试题解析
3. 下列运算中，正确的是（）

A、 $3 a^{2} + 2 a^{3} = 5 a^{5}$ B、 ${(- 3 a^{2} b^{3})}^{3} = - 9 a^{6} b^{9}$ C、 $(- 6 a^{3} b^{2}) \div (\frac{1}{2} a b^{2}) = - 3 a^{2}$ D、 $2 a^{2} b^{3} \cdot 4 a = 8 a^{3} b^{3}$

查看试题解析
4. 如图，△ABC中，点D、E分别在AB、AC上，DE $∥$ BC，DB＝2AD，则S_△ADE：S_△ABC＝（）

A、 $\frac{1}{9}$ B、 $\frac{1}{4}$ C、 $\frac{1}{6}$ D、 $\frac{1}{3}$

查看试题解析
5. 函数 $y = \frac{\sqrt{x + 2}}{x - 1}$ 的自变量取值范围是（）

A、 $x \geq - 2$ B、 $- 2 \leq x < 1$ C、 $x > 1$ D、 $x \geq - 2$ 且 $x \neq 1$

查看试题解析
6. 下列说法中，正确的是（）

A、“三角形的内角和为180°”是必然事件 B、神舟十三号飞船发射前的零件检查，可以选择抽样调查 C、为了反映近五年云南省财政收入变化趋势，适合采用扇形统计图 D、投掷一枚硬币10次，7次正面朝上，则投掷一枚硬币正面朝上的概率为0.7

查看试题解析
7. 不等式组 ${\begin{array}{l} - 2 x \leq 0 \\ 3 - x > 0 \end{array}$ 的整数解有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 如图，在矩形ABCD中，AB＝4cm，对角线AC与BD相交于点O，DE⊥AC，垂足为E，AE＝3CE，则DE的长为（）

A、 $\sqrt{3} c m$ B、2cm C、 $2 \sqrt{2} c m$ D、 $2 \sqrt{3} c m$

查看试题解析
9. 已知 $A_{5}^{3} = 5 \times 4 \times 3 = 60$ ， $A_{5}^{2} = 5 \times 4 = 20$ ， $A_{6}^{3} = 6 \times 5 \times 4 = 120$ ， $A_{9}^{4} = 9 \times 8 \times 7 \times 6 = 3024$ ， ……，观察并找规律，计算 $A_{7}^{3}$ 的结果是（）

A、42 B、120 C、210 D、840

查看试题解析
10. 如图，将△ABD沿△ABC的角平分线AD所在直线翻折，点B在AC边上的落点记为点E．已知∠C=20°、AB+BD=AC，那么∠B等于（）

A、80° B、60° C、40° D、30°

查看试题解析
11. “五一劳动节”期间，某校开展了以“劳动光荣”以主题的教育活动，该校组织全校教师和部分学生去郊区植树，已知老师平均每小时比学生多植5棵，且老师植树60棵所需的时间与学生植树45棵所需的时间相同，老师平均每小时植树（）

A、10棵 B、15棵 C、20棵 D、25棵

查看试题解析
12. 如图，正六边形ABCDEF的边长为6，以顶点A为圆心，AB的长为半径画弧，则由图中阴影部分的扇形围成的圆锥的高为（）

A、 $4 \sqrt{2}$ B、 $2 \sqrt{6}$ C、 $3 \sqrt{3}$ D、4

查看试题解析

二、填空题

13. $\sqrt{16}$ 的算术平方根是

查看试题解析
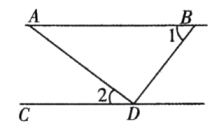
14. 如图， $A B ∥ C D$ ， AD⊥BD，∠1＝54°，则∠2的度数为．

查看试题解析
15. 因式分解： $2 x^{2} - 8 =$ .

查看试题解析
16. 如图，在 $△ A B C$ 中， $∠ A B C = 45 °$ ， F是高AD和BE的交点， $A C = 8$ cm，则线段BF的长度为．

查看试题解析
17. 若关于x的一元二次方程 $(m - 1) x^{2} + 4 x - 2 = 0$ 有两个相等的实数根，则m的值为．

查看试题解析
18. 在△ABC中，AB＝6，AC＝8，高AD＝4.8，设能完全覆盖△ABC的圆的半径为r，则r的最小值为．

查看试题解析

三、解答题

19. 点燃创业之火，实现人生梦想，李叔叔计划从甲、乙两家水果种植基地批发购进芒果若干筐，再选择A、B两家水果店进行出售．李叔叔分别从甲、乙两家水果种植基地批发的芒果随机抽取5筐进行检测，数据如下表：

水果基地	每筐芒果重量（千克）					平均数	中位数	方差
甲	24	25	26	26	25	a	25	c
乙	24	24	26	26	25	25	b	0.8

从A、B两家水果店了解到近5天芒果销售额相关数据如图：

根据以上图表信息，解答下列问题：

(1)、a＝；b＝；c＝；

(2)、根据统计图表中的数据，请问李叔叔如何选择芒果批发基地和销售商？并说明理由．

查看试题解析

20. 2022年4月16日，神舟十三号载人飞船返回舱在东风着陆场安全着陆，航天英雄翟志刚、王亚平、叶光富在空间站组合体工作生活了183天，创下了中国航天员连续在轨飞行时长新纪录，神舟十三号载人飞船飞行任务取得圆满成功．“筑梦向太空，致敬航天员”，某校为了庆祝神舟十三号完美着陆，组织班级选择A：《江山民心》、B：《一声令下》、C：《中国高度》三首歌曲中的一首进行合唱，甲、乙两个班级都申请参加本次合唱，学校决定两个班级各随机选择一首．

(1)、直接写出甲班恰好合唱《江山民心》的概率；

(2)、用列表或树状图法求出甲、乙两班都选择合唱《中国高度》的概率．

查看试题解析
21. 如图，在平面直角坐标系中，点A（1，a）在反比例函数 $y = \frac{6}{x}$ 的图像上，将点A先向右平移m个单位长度，再向下平移4个单位长度后得到点B，点B恰好落在反比例函数 $y = \frac{6}{x}$ 的图像上，连接AB．

(1)、求m的值；

(2)、点P是y轴上的点，连接PA、PB，请求出△PAB的周长最小时点P的坐标．

查看试题解析
22. 如图，AB是⊙O的直径，点C、D在⊙O上，且CD平分∠ACB，过点D作 $D E ∥ A B$ 交CB延长线于点E．

(1)、求证：DE是⊙O的切线；

(2)、若AC＝4， $t a n ∠ B A C = \frac{1}{2}$ ，求DE的长．

查看试题解析
23. 因为疫情，参加中考的学生进入考点需要检测体温，防疫部门为了了解学生进入考点进行体温检测的情况，调查了某个考点上午考生进入考点的累计人数y（人）与时间x（分钟）的变化情况，并绘制了如图所示图像．

(1)、研究发现9分钟内考生进入考点的累计人数是时间的二次函数，请求出9分钟内y与x之间的函数关系式；

(2)、如果考生一进考点就开始排队测量体温，体温监测点有2个，每个监测点每分钟检测20人，求排队人数最多时有多少人？全部考生都完成体温检测需要多少时间？

查看试题解析
24. 如图，在△ABC中，点D、E、F分别在边BC、AB、CA上，且 $D E ∥ C A$ ， $D F ∥ A B$ ．

(1)、若AD⊥BC于点D，且BD＝CD，求证：四边形AEDF是菱形；

(2)、若AE＝AF＝1，求 $\frac{1}{A B} + \frac{1}{A C}$ 的值；

(3)、设△BDE、△CDF、四边形AEDF的面积分别为 $S_{1}$ 、 $S_{2}$ 、S，求证： $S^{2} = 4 S_{1} S_{2}$ ．

查看试题解析