云南省昆明市盘龙区2022年初中学业水平考试模拟数学试题（二）

试卷更新日期：2022-05-30 类型：中考模拟

进入出卷网下载

一、单选题

1. 在 ${(\frac{1}{2})}^{- 1}$ ， -1， ${(- 6)}^{0}$ ， 0这四个数中，最小的数是（）

A、 ${(\frac{1}{2})}^{- 1}$ B、-1 C、 ${(- 6)}^{0}$ D、0

查看试题解析
2. 下列运算正确的是（）

A、 $\sqrt{4} = \pm 2$ B、 $\frac{1}{a + 1} + \frac{1}{1 - a} = 0$ C、 $x^{2} y^{3} \div 2 x y = \frac{1}{2} x y^{2}$ D、 ${(a - b)}^{2} = a^{2} - b^{2}$

查看试题解析
3. 如图是由5个形状大小完全相同的小正方体搭成的几何体，若将小正方形A移到小正方体B的正上方，则关于该几何体变化前后的三视图，下列说法正确的是（）

A、左视图不变 B、俯视图改变 C、主视图不变 D、以上三种视图都改变

查看试题解析
4. 将不等式组 ${\begin{array}{l} 2 x - 4 \geq 0 \\ \frac{1 - x}{3} < 1 \end{array}$ 中的两个不等式的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
5. 如图，正五边形ABCDE边长为6，以A为圆心，AB为半径画圆，图中阴影部分的面积为（）．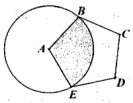

A、 $\frac{18}{5} π$ B、 $4 π$ C、 $\frac{54}{5} π$ D、 $12 π$

查看试题解析
6. 定义运算：m※n $= 2 m^{2} + m - n$ ．例如： 1※2 $= 2 \times 1^{2} - 1 - 2 = 1$ ．则方程x※2=0的根的情况为（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定

查看试题解析
7. 如图，已知BC＝BD，那么添加下列一个条件后，仍无法判定△ABC≌△ABD的是（）

A、AC＝AD B、∠ABC＝∠ABD C、∠C＝∠D＝90° D、∠CAB＝∠DAB

查看试题解析
8. 下列说法正确的是（）

A、若式子 $\sqrt{x - 1}$ 有意义，则x的取值范围是 $x > 1$ B、若点 $M (- 2 ， y_{1})$ 、点 $N (- 1 ， y_{2})$ 在双曲线 $y = \frac{k}{x} (k > 0)$ 的图象上，则 $y_{1} < y_{2}$ C、为了了解全国中学生的心理健康情况，应该采用普查的方式 D、甲、乙两人进行射击测试，每人10次，射击成绩的平均数都是8.6环，方差分别是 $S_{甲}^{2} = 0.45$ ， $S_{乙}^{2} = 0.50$ ，则射击成绩最稳定的是甲

查看试题解析
9. 下列图形都是由同样大小的黑色正方形纸片组成，其中图①有3张黑色正方形纸片，图②有5张黑色正方形纸片，图③有7张黑色正方形纸片，……按此规律排列下去，图ⓝ中黑色正方形纸片的张数为（）

A、 $2 n - 1$ B、 $2 n + 1$ C、 $2 n + 2$ D、 $2 n - 2$

查看试题解析
10. 我国古代《算法统宗》里有这样一首诗：“我问开店李三公，众客都来到店中，一房七客多七客，一房九客一房空．”诗中后两句的意思是：如果每一间客房住7人，那么有7人无房住；如果每一间客房住9人，那么就空出一间客房．设该店有客房x间、房客y人，下列方程组中正确的是（）

A、 ${\begin{matrix} 7 x + 7 = y \\ 9 (x - 1) = y \end{matrix}$ B、 ${\begin{matrix} 7 x + 7 = y \\ 9 (x + 1) = y \end{matrix}$ C、 ${\begin{matrix} 7 x - 7 = y \\ 9 (x - 1) = y \end{matrix}$ D、 ${\begin{matrix} 7 x - 7 = y \\ 9 (x + 1) = y \end{matrix}$

查看试题解析
11. 为了调查疫情对青少年人生观、价值观产生的影响，某学校团委对七年级学生进行了问卷调查，其中一项是：疫情期间出现的哪一个高频词汇最触动你的内心？针对该项调查结果制作出如下两幅不完整的统计图．由图中信息可知，下列结论错误的是（）

A、本次调查的样本容量是600 B、选“奉献”的有90人 C、扇形统计图中“感恩”所对应的扇形圆心角度数为108° D、选“感恩”的人数比选“敬畏”的人数多100人

查看试题解析
12. 东莞市某学校数学探究小组利用无人机在操场上开展测量教学楼高度的活动，如图，此时无人机在离地面30米的点D处，操控者站在点A处，无人机测得点A的俯角为30°，测得教学楼楼顶点C处的俯角为45°，操控者和教学楼BC的距离为60米，则教学楼BC的高度是（）米．

A、 $60 - 30 \sqrt{3}$ B、 $30 \sqrt{3}$ C、 $30 \sqrt{3} - 30$ D、 $30 \sqrt{3} - 15$

查看试题解析

二、填空题

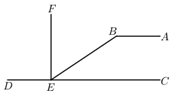
13. 据新华社消息，2022年北京冬奥会开幕式中国大陆地区观看人数约为316 000 000人，将数据316 000 000用科学记数法表示为．

查看试题解析
14. 如图，AB∥CD，∠ABE＝148°，FE⊥CD于E，则∠FEB的度数是度．

查看试题解析
15. 分解因式： $x y^{2} - 9 x =$ ．

查看试题解析
16. 如图，平行四边形ABCD中，AC、BD交于点O，分别以点A和点C为圆心，大于 $\frac{1}{2} A C$ 的长为半径作弧，两弧相交于M、N两点，作直线MN，交AB于点E，交CD于点F，连接CE，若AD＝6，△BCE的周长为14，则CD的长为．

查看试题解析
17. 已知点 $P (a ， b)$ 为反比例函数 $y = - \frac{5}{x}$ 与一次函数 $y = x - 7$ 的其中一个交点，则 $\frac{1}{b} - \frac{1}{a}$ 的值为．

查看试题解析
18. 如图，已知四边形 $A B C D$ 中， $A B = 10$ 厘米， $B C = 8$ 厘米， $C D = 12$ 厘米， $∠ B = ∠ C$ ，点 $E$ 为 $A B$ 的中点．如果点P在线段BC上以3厘米/秒的速度由B点向C点运动，同时，点Q在线段CD上由C点向D点运动．当点 $Q$ 的运动速度为厘米/秒时，能够使 $△ B E P$ 与 $△ C P Q$ 全等．

查看试题解析

三、解答题

19. 疫情后，某区针对各校在线教学进行评比，A校通过初评决定从甲、乙两个班中推荐一个班作为在线教学先进班级．下表是这两个班的四项指标的考评得分表（单位：分）
班级
课程质量
在线答疑
作业情况
课堂参考
甲班
10
5
10
7
乙班
8
8
9
7
四项指标的考评得分分析表：
班级
平均分
众数
中位数
甲班
$a$
10
$c$
乙班
8
$b$
8
请根据统计表中的信息解答下列问题：

(1)、填空：a= ， b= ， c=；

(2)、如果A校把“课程质量”、“在线答疑”、“作业情况”、“课堂参与”这四项指标得分按照2：3：2：3的比例确定最终成绩，请你通过计算判断应推荐哪个班为在线教学先进班级？

(3)、通过最终考评，A校总共36个班级里有3个班级获得在线教学先进班级，若该区所有学校总共有1200个班级数，估计该区总共有多少个班级可获得在线教学先进班级？

查看试题解析
20. 迄今为止，我国在航天领域获得的成就可谓硕果累累，当前探月、高分、北斗等航天领域国家科技重大专项任务圆满收官.在第六个“中国航天日”来临之际，某班举办了《我的航天梦，我的中国梦》演讲大赛，现有6人报名参加比赛，其中女生4人，男生2人.

(1)、若要从这6名选手中随机选择一位参赛，则选到女生的概率为；

(2)、经过一轮预选，甲、乙两人的演讲水平不相上下，现要在他们两人中选一人去参加全校的演讲比赛，班委会计划通过摸球的方式选派一人参加学校的演讲大赛.规则如下：
现有A、B两个不透明的袋子，A袋中装有3个小球，把它们分别标上数字1、2、3，B袋中装有4个小球，把它们分别标上数字1、2、3、4，这些小球除数字外其余完全相同.先由甲从A袋中随机摸出一个小球，记下小球上的数字；再由乙从B袋中随机摸出一个小球，记下小球上的数字，然后计算出这两个数字的和，若两个数字的和为奇数，则选甲去；若两个数字的和为偶数，则选乙去.请用列表法或画树状图的方法说明这个规则对双方是否公平.

查看试题解析
21. 如图，已知抛物线 $y = - \frac{1}{2} x^{2} + b x + c$ 经过点 $A (- 1 ， 0)$ 和点 $B (0 ， \frac{5}{2})$ ，顶点为C，点D在对称轴上且位于点C下方，将线段DC绕点D按顺时针方向旋转90°，点C恰好落在抛物线上的点P处．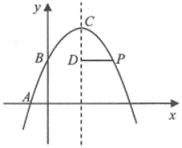

(1)、求这条抛物线的解析式及顶点C的坐标；

(2)、求线段CD的长．

查看试题解析
22. 如图，AB是⊙O的直径，C是⊙O上一点，OD⊥BC于点D，过点C作⊙O的切线，交OD的延长线于点E，连结BE.

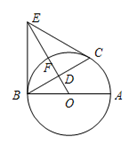(1)、求证：BE是⊙O的切线；

(2)、设OE交⊙O于点F，若DF＝2，BC＝ $4 \sqrt{3}$ ，求劣弧BC的长.

查看试题解析
23. 冰墩墩是2022年北就冬季奥运会的吉祥物．冰墩墩以熊猫为原型设计，寓意创造非凡、探索未来．某商店准备用2400元购进一批冰墩墩钥匙扣出售．假如每个钥匙扣的进价降低20%，则可以多买50个．

(1)、求每个冰墩墩钥匙扣的进价；

(2)、市场调查发现：当每个冰墩墩钥匙扣的售价是20元时，每周可以销售200个；每涨价1元，每周少销售10个．设每个冰墩墩钥匙扣的售价是x元（x是大于20的正整数），每周总利润是w元．
①求w与x的函数关系，并求每周总利润的最大值；
②当每周总利润大于1870元时，直接写出每个冰墩墩钥匙扣的售价．

查看试题解析
24. 在矩形ABCD的CD边上取一点E，将△BCE沿BE翻折，得到△BFE．已知 $A B = 6$ ， $B C = 10$ ．

(1)、若点F恰好在AD上；
①如图1，过点F作 $F O ∥ C D$ 交BE于点O，求证：四边形FOCE为菱形．
②如图2，延长EF，与 $∠ A B F$ 的角平分线交于点M，BM交AD于点N．请猜想NF与BC的关系，并说明理由；

(2)、如图3，若点F不在AD上， $∠ A B F$ 的角平分线交EF的延长线于点M，点E从点C运动到点D的过程中，直接写出点M运动的路径长．

查看试题解析

班级	课程质量	在线答疑	作业情况	课堂参考
甲班	10	5	10	7
乙班	8	8	9	7

班级	平均分	众数	中位数
甲班	$a$	10	$c$
乙班	8	$b$	8