云南省昆明市禄劝县2022年初中学业水平模拟数学试卷(二)
试卷更新日期:2022-05-30 类型:中考模拟
一、单选题
-
1. 如果把一个物体向右移动1m时记作移动+1m,那么这个物体向左移动2m时记作移动( )A、﹣1m B、+2m C、﹣2m D、+3m2. 下列几何图形既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图,将直尺与角的三角尺叠放在一起,若 , 则的大小是( )
3. 如图,将直尺与角的三角尺叠放在一起,若 , 则的大小是( ) A、 B、 C、 D、4. 式子:有意义时,的取值范围是( )A、 B、 C、且 D、 且5. 下列多边形中,内角和为720°的是( )A、
A、 B、 C、 D、4. 式子:有意义时,的取值范围是( )A、 B、 C、且 D、 且5. 下列多边形中,内角和为720°的是( )A、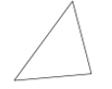 B、
B、 C、
C、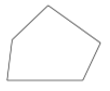 D、
D、 6. 某蔬菜种植基地2018年的蔬菜产量为800吨,2020年的蔬菜产量为968吨,设每年蔬菜产量的年平均增长率都为x,则年平均增长率x应满足的方程为( )A、 B、 C、 D、7. 如图,在平面直角坐标系中,△ABO的边OB与x轴重合,反比例函数y=kx经过线段AB的中点C.若△ABO的面积为6,则k的值为( )
6. 某蔬菜种植基地2018年的蔬菜产量为800吨,2020年的蔬菜产量为968吨,设每年蔬菜产量的年平均增长率都为x,则年平均增长率x应满足的方程为( )A、 B、 C、 D、7. 如图,在平面直角坐标系中,△ABO的边OB与x轴重合,反比例函数y=kx经过线段AB的中点C.若△ABO的面积为6,则k的值为( ) A、6 B、-6 C、3 D、-38. 下列运算正确的是( )A、 B、 C、 D、9. 大理古城是闻名遐迩的历史文化名城,春节期间相关部门对到大理观光的游客的出行方式进行了随机抽样调查,整理后绘制了两幅统计图(尚不完整),根据图中信息,下列结论错误的是( )
A、6 B、-6 C、3 D、-38. 下列运算正确的是( )A、 B、 C、 D、9. 大理古城是闻名遐迩的历史文化名城,春节期间相关部门对到大理观光的游客的出行方式进行了随机抽样调查,整理后绘制了两幅统计图(尚不完整),根据图中信息,下列结论错误的是( ) A、本次抽样调查的样本容量是5000 B、扇形统计图中的m为10% C、样本中选择公共交通出行的有2500人 D、若春节期间到大理观光的游客有60万人,则选择自驾方式出行的约有25万人10. 按一定规律排列的单项式: ,…第n个单项式是( )A、 B、 C、 D、11. 如图,在△ABC中, , , 分别以点A,点B为圆心,大于长为半径画弧,两弧相交于M,N两点连接MN交AC于D,交AB于E,连接BD,若 , 则BC的长为( ).
A、本次抽样调查的样本容量是5000 B、扇形统计图中的m为10% C、样本中选择公共交通出行的有2500人 D、若春节期间到大理观光的游客有60万人,则选择自驾方式出行的约有25万人10. 按一定规律排列的单项式: ,…第n个单项式是( )A、 B、 C、 D、11. 如图,在△ABC中, , , 分别以点A,点B为圆心,大于长为半径画弧,两弧相交于M,N两点连接MN交AC于D,交AB于E,连接BD,若 , 则BC的长为( ). A、8 B、7 C、4 D、312. 如图,四边形ABCD是矩形纸片, , 对折矩形纸片ABCD,使AD与BC重合,折痕为EF.展平后再过点B折叠矩形纸片,使点A落在EF上的点N,折痕为BM,再次展平,连接BN,MN,延长MN交BC于点G.有如下结论:①;②;③△BMG是等边三角形;④;⑤P为线段BM上一动点,H是线段BN上的动点,则的最小值是 . 其中正确结论有( )
A、8 B、7 C、4 D、312. 如图,四边形ABCD是矩形纸片, , 对折矩形纸片ABCD,使AD与BC重合,折痕为EF.展平后再过点B折叠矩形纸片,使点A落在EF上的点N,折痕为BM,再次展平,连接BN,MN,延长MN交BC于点G.有如下结论:①;②;③△BMG是等边三角形;④;⑤P为线段BM上一动点,H是线段BN上的动点,则的最小值是 . 其中正确结论有( ) A、①②③⑤ B、①②③④ C、①③④⑤ D、①②③④⑤
A、①②③⑤ B、①②③④ C、①③④⑤ D、①②③④⑤二、填空题
-
13. 将多项式因式分解为 .14. 若与互为相反数,则 .15. 已知某几何体的三视图如图所示,则该几何体的侧面展开图的半径是 .
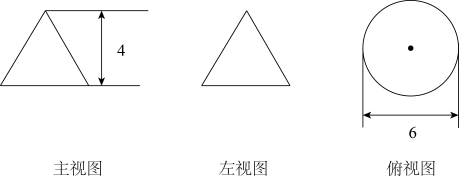 16. 分式方程解得 .17. 如图,在正方形ABCD中, , 对角线AC,BD交于点O.则图中阴影部分的面积为 .
16. 分式方程解得 .17. 如图,在正方形ABCD中, , 对角线AC,BD交于点O.则图中阴影部分的面积为 . 18. 四边形ABCD是平行四边形, , 的角平分线分别交BC边于点E和点F,若 , , 则四边形ABCD周长为 .
18. 四边形ABCD是平行四边形, , 的角平分线分别交BC边于点E和点F,若 , , 则四边形ABCD周长为 .三、解答题
-
19. 小明从商店里购买3张正面分别印有2022年北京冬奥会吉祥物卡片(卡片的形状、大小、质地都相同),其中印有“冰墩墩”图片的卡片2张、印有“雪容融”图片的卡片1张,将这三张正面卡片背面朝上、洗匀.
 (1)、若从中任意抽取1张,抽得卡片上的图案恰好为“冰墩墩”的概率是;(2)、若先从中任意抽取1张,记录后放回、洗匀,再从中任意抽取1张,请用树状图或列表的方法求两次抽取的卡片刚好是1张是“冰墩墩”另1张是“雪容融”的概率.20. 2021年中国共产党建党100周年,为了更好地对中学生开展党史学习教育活动,甲、乙两校进行了相关知识测试.在两校各随机抽取20名学生的测试成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.
(1)、若从中任意抽取1张,抽得卡片上的图案恰好为“冰墩墩”的概率是;(2)、若先从中任意抽取1张,记录后放回、洗匀,再从中任意抽取1张,请用树状图或列表的方法求两次抽取的卡片刚好是1张是“冰墩墩”另1张是“雪容融”的概率.20. 2021年中国共产党建党100周年,为了更好地对中学生开展党史学习教育活动,甲、乙两校进行了相关知识测试.在两校各随机抽取20名学生的测试成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.表1甲校学生样本成绩频数分布:
成绩m(分)
频数(人)
频率
0.05
3
0.15
8
0.40
6
0.30
合计
20
1.00
甲校成绩在的这一组的具体成绩是:
83 86 87 84 88 89 89 89
甲、乙两校成绩的统计数据如表2所示:
学校
平均分
中位数
众数
甲
83.7
89
乙
84.2
85
85
根据表中提供的信息,解答下列问题:
(1)、表1中;; .(2)、表2中,;在此次测试中,某学生的成绩是86分,在他所属学校排在前10名,由表中数据可知该学生是校的学生(填“甲”或“乙”);(3)、若甲校共有2200人,成绩不低于85分为“优秀”,则甲校成绩“优秀”的人数约为多少人?21. 如图,等腰△ABC中, , 交BC于D点,E点是AB的中点,分别过D,E两点作线段AC的垂线,垂足分别为G,F两点. (1)、求证:四边形DEFG为矩形;(2)、若 , , 求 .22. 冬奥会期间,冰墩墩玩偶非常畅销.小冬在某网店选中A,B两款冰墩墩玩偶,决定从该网店进货并销售.两款玩偶的进货价和销售价如下表:
(1)、求证:四边形DEFG为矩形;(2)、若 , , 求 .22. 冬奥会期间,冰墩墩玩偶非常畅销.小冬在某网店选中A,B两款冰墩墩玩偶,决定从该网店进货并销售.两款玩偶的进货价和销售价如下表:A款玩偶
B款玩偶
进货价(元/个)
20
15
销售价(元/个)
28
20
(1)、第一次小冬550元购进了A,B两款玩偶共30个,求两款玩偶各购进多少个.(2)、第二次小冬进货时,网店规定A款玩偶进货数量不得超过B款玩偶进货数量的一半.小冬计划购进两款玩偶共30个,应如何设计进货方案才能获得最大利润,最大利润是多少?

