云南省昆明市安宁市2022年初中学业水平第二次模拟考试数学试题
试卷更新日期:2022-05-30 类型:中考模拟
一、单选题
-
1. 4的算术平方根是( )A、-2 B、2 C、 D、2. 下列运算正确的是( )A、 B、 C、 D、3. 下列说法:
①一组数据2,2,3,4的中位数是2;
②一组数据的 , 4,1,4,2众数是4;
③若甲、乙两组数据的平均数相同, , , 则乙组数据较稳定;
④小明的三次数学检测成绩106分,110分,116分,这三次成绩的平均数是111分.其中正确的是( )
A、①② B、②③ C、②④ D、③④4. 若一个多边形的内角和是900°,则这个多边形的边数是( )A、5 B、6 C、7 D、85. 一把直尺和一块含30°角的直角三角板ABC如图所示摆放,直尺一边与三角板的两直角边分别交于点D和点E,另一边与三角板的两直角边分别交于点F和点A,且∠CED=35°,那么∠BAF的大小为( )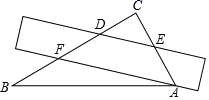 A、5° B、15° C、25° D、35°6. 观察下面算式,用你所发现的规律得出的末位数字是( )
A、5° B、15° C、25° D、35°6. 观察下面算式,用你所发现的规律得出的末位数字是( ), , , , , , , ,
A、 B、 C、 D、7. 若双曲线在第二、四象限,那么关于的方程的根的情况为( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、无实根8. 如图,在△ABC中,∠ACB=90°,分别以点A ,B为圆心,大于AB的长为半径作弧,两弧交于点M,N,作直线MN分别交AB,AC于点D,E,连接CD,BE,则下列结论中不一定正确的是( ) A、AD=BD B、BE>CD C、∠BEC=∠BDC D、BE平分∠CBD9. 如图,在 中,D、E分别是AB和AC的中点, ,则 ( )
A、AD=BD B、BE>CD C、∠BEC=∠BDC D、BE平分∠CBD9. 如图,在 中,D、E分别是AB和AC的中点, ,则 ( )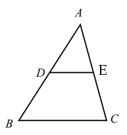 A、30 B、25 C、22.5 D、2010. 2017年,在创建文明城市的进程中,乌鲁木齐市为美化城市环境,计划种植树木30万棵,由于志愿者的加入,实际每天植树比原计划多20%,结果提前5天完成任务,设原计划每天植树x万棵,可列方程是( )A、 B、 C、 D、11. 构建几何图形解决代数问题是“数形结合”思想的重要性,在计算tan15°时,如图.在Rt△ACB中,∠C=90°,∠ABC=30°,延长CB使BD=AB , 连接AD , 得∠D=15°,所以tan15° .类比这种方法,计算tan22.5°的值为( )
A、30 B、25 C、22.5 D、2010. 2017年,在创建文明城市的进程中,乌鲁木齐市为美化城市环境,计划种植树木30万棵,由于志愿者的加入,实际每天植树比原计划多20%,结果提前5天完成任务,设原计划每天植树x万棵,可列方程是( )A、 B、 C、 D、11. 构建几何图形解决代数问题是“数形结合”思想的重要性,在计算tan15°时,如图.在Rt△ACB中,∠C=90°,∠ABC=30°,延长CB使BD=AB , 连接AD , 得∠D=15°,所以tan15° .类比这种方法,计算tan22.5°的值为( ) A、 B、 ﹣1 C、 D、12. 如图,在扇形BOC中,∠BOC=60°,OD平分∠BOC交于点D,点E为半径OB上一动点,若OB=2,则阴影部分周长的最小值为( )
A、 B、 ﹣1 C、 D、12. 如图,在扇形BOC中,∠BOC=60°,OD平分∠BOC交于点D,点E为半径OB上一动点,若OB=2,则阴影部分周长的最小值为( )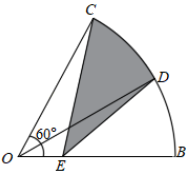 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
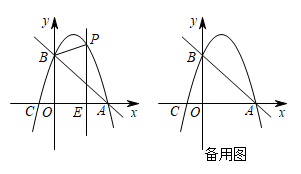
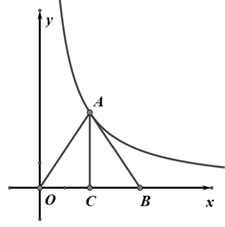
13. 因式分解: =.14. 已知|x+2y|+(x﹣4)2=0,则xy= .15. 不等式组 的解集为.16. 如图,在平面直角坐标系中,O是坐标原点,在 中, 于点C,点A在反比例函数 的图象上,若OB=4,AC=3,则k的值为.
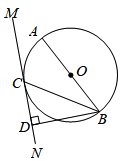
 17. 如图,内接于 , , , 则阴影部分的面积为 .
17. 如图,内接于 , , , 则阴影部分的面积为 .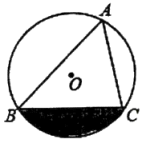 18. 在中, , , , 为的中点,为上一点,当构成的四边形有一组邻边相等时,的长为 .
18. 在中, , , , 为的中点,为上一点,当构成的四边形有一组邻边相等时,的长为 .三、解答题
-
19. 2022年2月分,由境外输入的“奥密克戎”病毒变异株,引发我国多地出现本土新冠病例.为做好2022年春季学期学校的疫情防控工作.某校开展学习防疫知识活动.为了解这次活动的效果,从全校学生中随机抽取部分学生进行测试,并将测试成绩统计如下:按成绩分成: , : , : , : , :五个等级,并绘制了如下不完整的两幅统计图.
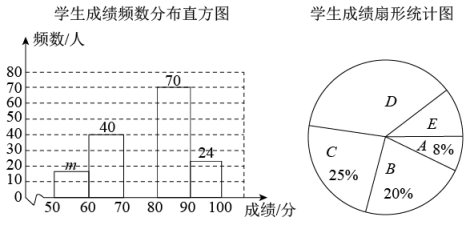
请结合统计图,解答下列问题:
(1)、本次调查一共随机抽取了名学生的成绩,频数分布直方图中;(2)、补全学生成绩频数分布直方图,在扇形统计图中,等级E对应的扇形圆心角度数是 ▲ ;(3)、如果成绩分为优秀,请通过计算估计全校2000名学生中成绩优秀的人数为人.20. 有4张不透明的卡片A、、、 , 它们除正面上的图案不同外,其他均相同.现将这4张卡片背面向上洗匀后放在桌面上.小明先从中随机取出一张卡片,记下标号,然后放回洗匀,接着由小丽从中随机再取出一张卡片,记下标号.

 (1)、用列表或树状图(树状图也称树形图)中的一种方法,求出所有可能出现的结果总数;(2)、求两次所抽取的卡片上的图案恰好都是轴对称图形的概率.21. 如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.
(1)、用列表或树状图(树状图也称树形图)中的一种方法,求出所有可能出现的结果总数;(2)、求两次所抽取的卡片上的图案恰好都是轴对称图形的概率.21. 如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.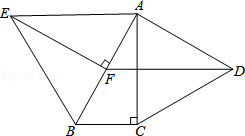 (1)、试说明AC=EF;(2)、求证:四边形ADFE是平行四边形.22. 2022年,冬奥会和冬残奥会在北京举办,冬奥会吉祥物“冰墩墩”和冬残奥会吉祥物“雪容融”深受广大人民的喜爱.2021年11月初,奥林匹克官方旗舰店上架了“冰墩墩”和“雪容融”这两款毛绒玩具,当月售出了“冰墩墩”200个和“雪容融”100个,销售总额为33000元.十二月售出了“冰墩墩”300个和“雪容融”200个,销售总额为54000元.(1)、求“冰墩墩”和“雪容融”的销售单价;(2)、已知“冰墩墩”和“雪容融”的成本分别为90元/个和60元/个,进入2022年1月后,这两款毛绒玩具持续热销,于是旗舰店准备用60000元全部购进这两款毛绒玩具.设购进“冰墩墩”x个,“雪容融”y个.
(1)、试说明AC=EF;(2)、求证:四边形ADFE是平行四边形.22. 2022年,冬奥会和冬残奥会在北京举办,冬奥会吉祥物“冰墩墩”和冬残奥会吉祥物“雪容融”深受广大人民的喜爱.2021年11月初,奥林匹克官方旗舰店上架了“冰墩墩”和“雪容融”这两款毛绒玩具,当月售出了“冰墩墩”200个和“雪容融”100个,销售总额为33000元.十二月售出了“冰墩墩”300个和“雪容融”200个,销售总额为54000元.(1)、求“冰墩墩”和“雪容融”的销售单价;(2)、已知“冰墩墩”和“雪容融”的成本分别为90元/个和60元/个,进入2022年1月后,这两款毛绒玩具持续热销,于是旗舰店准备用60000元全部购进这两款毛绒玩具.设购进“冰墩墩”x个,“雪容融”y个.①求y关于x的函数关系式;
②该旗舰店进货时,厂家要求“雪容融”的购进数量不超过“冰墩墩”的购进数量,若1月份购进的这两款毛绒玩具全部售出,则如何设计进货方案才能使该旗舰店当月销售利润最大,并求出最大利润.