云南省红河州2022年第二次初中学业水平模拟考试数学试题

试卷更新日期：2022-05-30 类型：中考模拟

进入出卷网下载

一、单选题

1. 某单位开展了“健步迎冬奥，一起向未来”职工健步走活动，职工每天健步走5000步即为达标．若小王走了7205步，记为+2205步；小李走了4700步，记为（）

A、-4700步 B、-300步 C、300步 D、4700步

查看试题解析
2. 如图，将木条a，b与c钉在一起， $∠ 2 = 48 °$ ，若要使木条a与b平行，则 $∠ 1$ 的度数应为（）

A、142° B、90° C、48° D、42°

查看试题解析
3. 数学课上陈老师要求学生利用尺规作图，作一个已知角的角平分线，并保留作图痕迹．学生小敏的作法是：如图， $∠ A O B$ 是已知角，以O为圆心，任意长为半径作弧，与OA、OB分别交于N、M；再分别以N、M为圆心，大于 $\frac{1}{2} M N$ 的长为半径作弧，交于点C；作射线OC；则射线OC是 $∠ A O B$ 的角平分线．小敏作图的依据是（）

A、SAS B、ASA C、AAS D、SSS

查看试题解析
4. 已知 $| a | = 1$ ， b是 $- \frac{1}{2}$ 的相反数，则a+b的值为（）

A、 $\frac{3}{2}$ 或 $- \frac{1}{2}$ B、 $\frac{3}{2}$ C、 $- \frac{1}{2}$ D、 $- \frac{3}{2}$ 或 $\frac{1}{2}$

查看试题解析
5. 下列几何体中的主（正）视图，是轴对称图形但不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
6. 化简 $(m - \frac{2 m n - n^{2}}{m}) \div \frac{m^{2} - n^{2}}{m^{2} + m n}$ 的正确结果是（）

A、m－n B、m+n C、 $\frac{1}{m - n}$ D、 $\frac{1}{m + n}$

查看试题解析
7. 如图，点O是矩形ABCD的对角线AC的中点， $O M ∥ A B$ 交AD于点M，若OM＝3，OB＝4，则BC的长为（）

A、5 B、 $2 \sqrt{7}$ C、8 D、10

查看试题解析
8. 从一个多边形的任何一个顶点出发都只有3条对角线，则它的内角和是（）

A、360° B、540° C、720° D、900°

查看试题解析
9. 如图，在 $△ A B C$ 中， $c o s B = \frac{4}{5}$ ， $t a n C = \sqrt{3}$ ， AB＝5，则AC的长为（）

A、3 B、4 C、 $\sqrt{3}$ D、 $2 \sqrt{3}$

查看试题解析
10. 如图，反比例函数 $y = \frac{k}{x} (x < 0)$ 与一次函数 $y = x + 4 (x < 0)$ 的图象交于A、B两点的横坐标分别为－3、－1，则关于x的不等式 $\frac{k}{x} < x + 4 (x < 0)$ 的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
11. 如图， $R t △ B C O$ 中， $∠ B C O = 90 °$ ， $∠ C B O = 30 °$ ， BO＝2cm，将 $△ B C O$ 绕点O逆时针旋转至 $△ B^{'} C^{'} O$ ，点 $C^{'}$ 在BO的延长线上，则边BC扫过区域（图中阴影部分）的面积为（）

A、 $π c m^{2}$ B、 $(\frac{\sqrt{3}}{2} + π) c m^{2}$ C、 $2 π c m^{2}$ D、 $(\frac{\sqrt{3}}{2} + 2 π) c m^{2}$

查看试题解析
12. 如图，在平面直角坐标系中，矩形ABOC的顶点A的坐标为 $(- 2 ， 4)$ ， D是OB的中点，E是OC上的一点，当 $△ A D E$ 的周长最小时，点E的坐标是（）

A、 $(0 ， 1)$ B、 $(0 ， \frac{4}{3})$ C、 $(0 ， 2)$ D、 $(0 ， \frac{10}{3})$

查看试题解析

二、填空题

13. 某新型冠状病的直径大为0.00000012米，0.00000012这个数据用科学记数法可表示为.

查看试题解析
14. 如图，已知点A在反比例函数 $y = \frac{k}{x} (k < 0)$ 的图象上， $A C ⊥ y$ 轴于点C，点B在x轴的负半轴上，若 $S_{△ A B C} = 4$ ，则k的值为．

查看试题解析
15. 下图是由一些火柴棒摆成的图案，按照这样的方式摆下去，摆第 $n$ 个图案需要火柴棒的根数为．

查看试题解析
16. 关于x的一元二次方程 $x^{m + 2} + 2 x - n = 0$ 有两个相等的实数根，则 ${(\frac{1}{3})}^{m} + {(\frac{1}{2})}^{n}$ 的值为．

查看试题解析
17. 符号“ $| \begin{array}{l} a & b \\ c & d \end{array} |$ ”称为二阶行列式，规定它的运算法则为： $| \begin{array}{l} a & b \\ c & d \end{array} | = a d - b c$ ，请你根据运算法则求出等式中x的值．若 $| \begin{array}{l} 2 & 1 \\ \frac{3}{x + 1} & \frac{1}{x + 1} \end{array} | = 1$ ，那么x＝．

查看试题解析
18. 如图，在正方形ABCD中，AB＝6，连接对角线AC、BD相交于点O，点P是正方形边上或对角线上的一点，若 $\frac{P D}{A P} = 2$ ，则AP＝．

查看试题解析

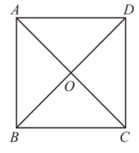
三、解答题

19. 近日，俄乌军事冲突事件引起了全世界的关注，此次事件也让我们深切体会到：只有祖国强大了，人民群众才能安居乐业．某校组织七、八年级各200名学生举行了“少年强则国强”演讲比赛．现分别在七、八两个年级中各随机抽取了10名学生，统计这部分学生的比赛成绩，相关数据统计、整理如下：
【收集数据】
七年级10名同学比赛成绩统计如下：72，83，72，92，79，69，78，85，76，94；
八年级10名同学比赛成绩统计如下：86，71，93，83，80，74，75，80，76，82．
【整理数据】两组数据各分数段，如表所示：
成绩
$60 \leq x < 70$
$70 \leq x < 80$
$80 \leq x < 90$
$90 \leq x < 100$
七年级
1
5
a
2
八年级
0
4
5
1
【分析数据】两组数据的平均数、中位数、众数、方差如表：
统计量年级
平均数
中位数
众数
方差
七年级
80
c
72
64.4
八年级
b
80
d
37.6
【问题解决】根据以上信息完成下列问题：

(1)、a＝， b＝， c＝， d＝；

(2)、请你估计哪个年级的比赛成绩更稳定；

(3)、按照比赛规定90分及其以上算优秀，请估计这两个年级比赛成绩达到优秀学生的人数共有多少人？

查看试题解析
20. 现有四张正面分别标有数字－3，－2，－1，2的不透明卡片，它们除数字外其余完全相同，将他们背面朝上洗均匀后，随机抽取两张，记上面的数字分别为m，n．

(1)、用列表法或树状图法（树状图也称树形图）中的一种方法，写出所有可能出现的结果；

(2)、请求出使代数式 $\frac{\sqrt{m - n}}{3}$ 有意义的概率．

查看试题解析
21. 如图， $△ A B C$ 内接于⊙ $O$ ， ⊙ $O$ 的直径AD与弦BC相交于点E，BE＝CE，过点D作 $D F ∥ B C$ 交AC的延长线于点F．

(1)、求证：DF是⊙ $O$ 的切线；

(2)、若 $s i n ∠ B A D = \frac{1}{3}$ ， AB＝6，求DF的长．

查看试题解析
22. 滇池是云南最大的淡水湖，素有“高原明珠”的称号．每年冬天，来自西伯利亚的红嘴鸡都会随着季节的变化来滇池过冬，但滇池污染问题严重，为了更好地治理滇池，保护环境，综合治理指挥部决定购买10台污水处理设备．现有A、B两种型号的设备，其中A型设备每台每月可处理污水220吨，B型设备每台每月可处理污水180吨．经调查：购买一台A型设备比购买一台B型设备多2万元，购买2台A型设备比购买3台B型设备少6万元．

(1)、请分别求出购买一台A型设备和B型设备的价格；

(2)、设购买A型设备x台，A、B两种型号的设备每月总共能处理污水y吨．求y与x之间的函数关系式，并直接写出x的取值范围；

(3)、由于受资金限制，河道综合治理指挥部决定购买污水处理设备的总资金不超过110万元，则每月最多能处理污水多少吨？

查看试题解析
23. 图1，矩形纸片ABCD，AB＝4，BC＝8，点M、N分别在矩形的边AD、BC上，将矩形纸片沿直线MN折叠，使点C落在矩形的边AD上，记为点P，点D落在点G处，连接PC，交MN于点Q，连接CM．

(1)、求证：四边形CMPN是菱形；

(2)、如图2，当点P与点A重合时，求四边形CMPN的面积．

查看试题解析
24. 有一组邻边相等的凸四边形叫做“和睦四边形”，如菱形，正方形等都是“和睦四边形”．

(1)、如图1，BD平分 $∠ A B C$ ， $A D ∥ B C$ ，求证：四边形ABCD为“和睦四边形”；

(2)、如图2，直线AB与x轴，y轴分别交于 $A (12 ， 0)$ ， $B (0 ， 9)$ 两点，点P、Q分别是线段OA、AB上的动点．点P从点A出发，以每秒4个单位长度的速度向点O运动．点Q从点A出发，以每秒5个单位长度的速度向点B运动．P，Q两点同时出发，设运动时间为t秒，当四边形BOPQ为“和睦四边形”时，求t的值；

(3)、如图3，抛物线 $y = a x^{2} + \frac{2 \sqrt{3}}{3} x + 2 (a < 0)$ 与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，抛物线的顶点为点D．当四边形COBD为“和睦四边形”，且CD＝OC，求a的值．

查看试题解析

成绩	$60 \leq x < 70$	$70 \leq x < 80$	$80 \leq x < 90$	$90 \leq x < 100$
七年级	1	5	a	2
八年级	0	4	5	1

统计量年级	平均数	中位数	众数	方差
七年级	80	c	72	64.4
八年级	b	80	d	37.6