山西省太原市2022年九年级下学期一模数学试题

试卷更新日期：2022-05-30 类型：中考模拟

进入出卷网下载

一、单选题

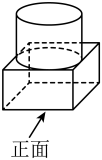
1. 下列各数中，绝对值最小的数是（）

A、0 B、-1 C、-5 D、2

查看试题解析
2. 下列运算正确的是（）

A、 $(- a)^{3} \cdot a^{2} = a^{5}$ B、 $2 a + a = 2 a^{2}$ C、 $- a (2 a - 5) = - 2 a^{2} + 5 a$ D、 $(2 a + 3 b) (a - 2 b) = 2 a^{2} - 7 a b - 6 b^{2}$

查看试题解析
3. 由圆柱和长方体（底面为正方形）组成的几何体如图放置，该几何体的俯视图是（）

A、 B、 C、 D、

查看试题解析
4. 中国人很早就开始使用负数，魏晋时期的数学家刘徽在“正负术”的注文中指出，可将算筹（小棍形状的记数工具）正放着表示正数，斜放着表示负数，如图（1）表示 $(+ 2) + (- 2)$ ．按照这种表示法，如图（2）表示的是（）

A、 $(+ 3) + (+ 6)$ B、 $(- 3) + (- 6)$ C、 $(- 3) + (+ 6)$ D、 $(+ 3) + (- 6)$

查看试题解析
5. “又是一年三月三”．在校内劳动课上，小明所在小组的同学们设计了如图所示的风筝框架．已知 $∠ B = ∠ E ， A B = D E ， B F = E C ， △ A B C$ 的周长为 $24 c m$ ， $F C = 3 c m$ ．制作该风筝框架需用材料的总长度至少为（）

A、 $44 c m$ B、 $45 c m$ C、 $46 c m$ D、 $48 c m$

查看试题解析
6. 一个机器人在一条直线上移动，每次只能向左或向右移动一个单位长度，移动2次后它回到出发位置的概率等于（）

A、 $\frac{2}{3}$ B、 $\frac{1}{2}$ C、 $\frac{1}{4}$ D、 $\frac{1}{8}$

查看试题解析
7. 圆的周长公式是人类文明进程中最伟大的公式之一．现在计算圆周率的精确度主要用于检验计算机的运算速度，目前人类能够计算到圆周率的628万亿位．把数据“62.8万亿”用科学记数法表示为（）

A、 $6.28 \times 1 0^{8}$ B、 $6.28 \times 1 0^{9}$ C、 $6.28 \times 1 0^{13}$ D、 $6.28 \times 1 0^{14}$

查看试题解析
8. 如图，用若干个全等的正五边形排成圆环状，图中所示的是其中3个正五边形的位置．若完成这一圆环排列，共需要正五边形的个数是（）

A、7个 B、8个 C、9个 D、10个

查看试题解析
9. 化简 $(\frac{x^{2} - 4}{x^{2} + 4 x + 4} + \frac{2}{x + 2}) \div \frac{x}{2 x + 4}$ 的结果是（）

A、2 B、 $\frac{2 x - 8}{x}$ C、 $- 6$ D、 $- 8$

查看试题解析
10. 在平面直角坐标系中，将抛物线 $y = a x^{2} + b x + c$ 先沿x轴向右平移3个单位长度，再沿y轴向上平移2个单位长度，得到抛物线 $y = x^{2} - 2 x - 4$ ，则抛物线 $y = a x^{2} + b x + c$ 的函数表达式为（）

A、 $y = x^{2} + 2 x + 4$ B、 $y = x^{2} + 4 x - 3$ C、 $y = x^{2} - 4 x + 3$ D、 $y = x^{2} - 8 x + 13$

查看试题解析

二、填空题

11. 不等式组 ${\begin{array}{l} x \geq 2 \\ 3 x - 2 < 2 x + 3 \end{array}$ 的解集是．

查看试题解析
12. 在课后服务时间，甲乙两班进行篮球比赛，在选择比赛场地时，裁判员采用了同时掷两枚完全相同硬币的方法：如果两枚硬币朝上的面不同，则甲班优先选择场地；否则乙班优先选择场地．这种选择场地的方法对两个班级（填“公平”或“不公平”）．

查看试题解析
13. 已知反比例函数 $y = \frac{5}{x}$ 的图像经过点 $A (x_{1} ， y_{1}) ， B (x_{2} ， y_{2})$ ，当 $x_{1} < 0 < x_{2}$ ，时，则 $y_{1}$ 与 $y_{2}$ 的大小关系是．

查看试题解析
14. 在2022年北京冬奥会期间，小明正好读到科赫曲线的相关内容．如图（1），线段的长为a，将其三等分，以中间一段为边作等边三角形．再把中间这段移去，生成了如图（2）所示的一条折线段，称为“一次构造”；用同样的方法把图（2）中每条线段进行操作，得到如图（3）所示的一条折线段，称为“二次构造”；…如此操作下去，经过“十次构造”生成的折线段的长为（用含a的代数式表示）．

查看试题解析
15. 如图， $A B$ 为 $⊙ O$ 的直径，C为 $⊙ O$ 上一点， $⊙ O$ 的切线 $B D$ 交 $A C$ 的延长线于点D，E为 $B D$ 的中点， $C E$ 交 $A B$ 的延长线于点F．若 $A C = 4$ ， $O B = B F$ ，则 $B D$ 的长为．

查看试题解析

三、解答题

16.

(1)、计算：

2^{0} - {(\frac{1}{3})}^{- 2} + (\sqrt{7} - 1) (\sqrt{7} + 1)

；

(2)、下面是小明同学解方程

\frac{x + 3}{2} - \frac{5 x - 3}{6} = 1

的过程，请认真阅读，并完成相应的任务．

解：去分母，得 $3 (x + 3) - (5 x - 3) = 1$ ．第一步

去括号，得 $3 x + 9 - 5 x + 3 = 1$ ．第二步

移项，得 $3 x - 5 x = - 9 - 3 + 1$ ．第三步

合并同类项．得 $- 2 x = - 11$ ．第四步

系数化为1，得 $x = \frac{2}{11}$ ．第五步

任务一：①解答过程中，第 ▲ 步开始出现了错误，产生错误的原因是 ▲ ；

②第三步变形的依据是 ▲ ．

任务二：①该一元一次方程的解是 ▲ ；

②写出一条解一元一次方程时应注意的事项．

查看试题解析

17. 北京冬奥会和冬残奥会期间，吉祥物冰嫩嫩和雪容融成了名副其实的国民顶流．最近，小李从某网站上发现正在预售A，B两种印有吉祥物图案的挂件．如果定购3件A种挂件和2件B种挂件，需支付360元；如果定购2件A种挂件和3件B种挂件，需支付370元．求这两种挂件每件的售价．

查看试题解析
18. 已知一个面积为1的矩形，当矩形的一边长为多少时，它的周长最小？最小值是多少？设一边长为x，周长为y，则 $y = 2 x + \frac{2}{x} (x > 0)$ ．我们可以借鉴研究函数的经验，利用图象的直观性探究函数 $y = 2 x + \frac{2}{x} (x > 0)$ 的性质，解决这个问题．

(1)、填写下表，并在如图的平面直角坐标系中画出函数图象：
x
…
0.2
0.5
1
1.5
2
3
…
y
…
10.4
4
5
…

(2)、结合图象，写出该函数两条不同类型的性质：
性质一：
性质二：

(3)、根据图象，当 $x =$ 时，周长有最小值，最小值等于．

查看试题解析
19. 某校在调查八年级学生平均每天完成作业所用时间的情况时，从全校八年级学生中随机抽取了n名学生，把每名学生平均每天完成作业的时间t（分钟）分成五个时间段进行统计：A． $50 \leq t < 60$ ， B． $60 \leq t < 70$ ， C． $70 \leq t < 80$ ， D． $80 \leq t < 90$ ， E． $90 \leq t < 100$ ，并制成如下两幅不完整的统计图．
根据上述信息，解答下列问题：

(1)、求n的值并补全条形统计图；

(2)、在扇形统计图中，时间段C所占的百分比 $(m)$ 为，时间段D所对应的圆心角的度数等于；

(3)、小颖同学经过分析得出一个推断：这组数据的众数落在时间段C．请你分析她的推断是否合理．

查看试题解析
20. 2022年底，太忻一体化经济区将新建1994座5G基站．如图是建在坡度 $i = 1 ： 2.4$ 的斜坡 $A M$ 上的一个5G基站塔 $C D$ ，在坡角顶点A处测得塔顶D的仰角为 $45 °$ ，沿斜坡步行 $52 m$ 到达B处，在B处测得塔顶D的仰角为 $63.4 °$ ，点A，B，C，D，M，N在同一平面内．求基站塔高 $C D$ ．
（结果精确到 $0.1 m$ ，参考数据： $s i n 63.4 ° = 0.89 ， c o s 63.4 ° = 0.45 ， t a n 63.4 ° \approx 2.00$ ）

查看试题解析
21. 阅读与证明
三大作图问题之三等分角三等分任意角是古希腊学者们于公元前5世纪提出并研究的三大作图问题之一．两千多年以来，数学家们为此耗费了许多心血．直到1837年，法国数学家闻脱兹尔证明了，只使用直尺和圆规无法三等分一个任意角，至此人类才走出了这座数学迷宫，在探究过程中发现，有些特殊度数的角如90°角，45°角， 108°角等可用尺规三等分，任意角采用特殊的工具也可三等分．

如图（1）， $∠ A B C$ ，下面是两种三等分角的方法．

(1)、阿基米德创设的方法是：在图（2）中，预先在直尺上作了一个记号点P，点O为直尺的端点，以B为圆心， $O P$ 为半径作半圆，与边 $B A$ 和 $B C$ 分别交于点N和M；移动直尺，使直尺上的点O在边 $B C$ 的反向延长线上移动，点P在圆周上，当直尺正好经过点N时，过点B画 $O N$ 的平行线 $B E$ ．求证： $∠ E B C = \frac{1}{3} ∠ A B C$ ；

(2)、用“有刻度的勾尺”的方法是：在图（3）中，勾尺的直角顶点为点P， $M N ⊥ P R$ 于点Q， $P Q = Q R$ ．画直线 $D E ∥ B C$ ，并且 $D E$ 与 $B C$ 之间的距离等于 $P Q$ ，移动勾尺到合适位置，使顶点P落在 $D E$ 上，使勾尺的边 $M N$ 经过点B，同时让点R落在边 $B A$ 上．求证： $∠ R B Q = \frac{1}{3} ∠ A B C$ ．

查看试题解析
22. 综合与探究
问题情境，如图，在矩形纸片ABCD中，点E，F分别是边AD，BC上的动点，连接EF，BE，DF．将矩形纸片ABCD分别沿直线BE，DF折叠，点A的对应点为点M，点C的对应点为点N．

(1)、操作探究：如图（1），若点F与点M重合， $D N$ 与 $E F$ 交于点G，求证：DG=GM；

(2)、探究发现：如图（2），当点M，N落在对角线 $B D$ 上时，判断并证明四边形 $B F D E$ 的形状；

(3)、探究拓广：当点M，N落在对角线 $A C$ 上时．
①在图（3）中补全图形；
②若 $A B = 2$ ， $A D = 3$ ，求 $△ B E F$ 的面积．

查看试题解析
23. 综合与实践
如图，抛物线 $y = x^{2} + 2 x - 8$ 与x轴交于A，B两点（点A在点B左侧），与y轴交于点C．点D在直线 $A C$ 下方的抛物线上运动，过点D作y轴的平行线交 $A C$ 于点E．

(1)、求直线 $A C$ 的函数表达式；

(2)、求线段 $D E$ 的最大值；

(3)、当点F在抛物线的对称轴上运动，以点A，C，F为顶点的三角形是直角三角形时，直接写出点F的坐标．

查看试题解析

x	…	0.2	0.5	1	1.5	2	3	…
y	…	10.4		4		5		…