山西省百校联考2022年第二次考试数学试卷
试卷更新日期:2022-05-30 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、 B、 C、 D、2. 观察下列图案,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图,直线 , 直线c分别与a,b相交于点A,B.若 , 则的度数为( )
3. 如图,直线 , 直线c分别与a,b相交于点A,B.若 , 则的度数为( ) A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 据央视新闻报道,2022届高校毕业生规模预计1 076万人,同比增加167万人.这是高校毕业生规模首次超过千万,也是近几年增长人数最多的一年.数据1 076万人用科学记数法表示为( )
A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 据央视新闻报道,2022届高校毕业生规模预计1 076万人,同比增加167万人.这是高校毕业生规模首次超过千万,也是近几年增长人数最多的一年.数据1 076万人用科学记数法表示为( ) A、人 B、人 C、人 D、人6. 下图是由8个大小相同的小正方体搭成的几何体,则这个几何体的主视图是( )
A、人 B、人 C、人 D、人6. 下图是由8个大小相同的小正方体搭成的几何体,则这个几何体的主视图是( )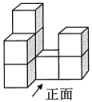 A、
A、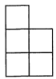 B、
B、 C、
C、 D、
D、 7. 若关于x的不等式组的解集表示在数轴上如图所示,则这个不等式组的解集是( )
7. 若关于x的不等式组的解集表示在数轴上如图所示,则这个不等式组的解集是( ) A、 B、 C、 D、8. 如图,某“综合与实践”小组为测量河两岸A,P两点间的距离,在点A所在岸边的平地上取点B、C、D,使A、B、C在同一条直线上,且;使且P、B、D三点在同一条直线上.若测得m,m,m,则A、P两点间的距离为( )
A、 B、 C、 D、8. 如图,某“综合与实践”小组为测量河两岸A,P两点间的距离,在点A所在岸边的平地上取点B、C、D,使A、B、C在同一条直线上,且;使且P、B、D三点在同一条直线上.若测得m,m,m,则A、P两点间的距离为( )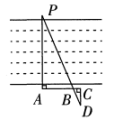 A、 B、 C、 D、9. 用配方法将二次函数化为的形式为( )A、 B、 C、 D、10. 如图,是的直径,点C是上一点,且点D是的中点,过点D作的切线与的延长线交于点E,连接 . 若 , , 则直径的长为( )
A、 B、 C、 D、9. 用配方法将二次函数化为的形式为( )A、 B、 C、 D、10. 如图,是的直径,点C是上一点,且点D是的中点,过点D作的切线与的延长线交于点E,连接 . 若 , , 则直径的长为( ) A、12 B、 C、 D、
A、12 B、 C、 D、二、填空题
-
11. 计算的结果为 .12. 若正多边形的每一个内角为 ,则这个正多边形的边数是 .13. 某公司招聘员工,采取笔试与面试相结合的方式进行,两项成绩的满分均为100分.编号为①,②,③的三名应聘者的成绩如下:
应聘者
项目
①
②
③
笔试成绩/分
85
92
90
面试成绩/分
90
85
90
根据该公司规定,笔试成绩和面试成绩分别按80%和20%的比例折合成综合成绩,那么这三名应聘者中第一名的成绩是分.
14. 如图,在扇形中,半径 , 点B是上一点,平分 . 点D,C在上,点E,F分别在半径和上;连接 , 其中与交于点P,与交于点H,且四边形和都是正方形;以线段为直径作半圆,连接 , 则图中阴影部分的面积为 . 15. 如图,在和中, , , , 且点B,C,E在同一条直线上,与交于点F,连接、 , 若 , . 则的长为 .
15. 如图,在和中, , , , 且点B,C,E在同一条直线上,与交于点F,连接、 , 若 , . 则的长为 .
三、解答题
-
16.(1)、计算: .(2)、先化简,再求值: , 其中 .17. 如图,一次函数的图象分别与x轴、y轴相交于点C,D,与反比例函数的图象相交于点 .
 (1)、求一次函数的表达式.(2)、当x为何值时,?请直接写出x的取值范围.18. 如图,矩形是某会展中心一楼展区的平面示意图,其中边的长为40米,边的长为25米,该展区内有三个全等的矩形展位,每个展位的面积都为200平方米,阴影部分为宽度相等的人行通道,求人行通道的宽度.
(1)、求一次函数的表达式.(2)、当x为何值时,?请直接写出x的取值范围.18. 如图,矩形是某会展中心一楼展区的平面示意图,其中边的长为40米,边的长为25米,该展区内有三个全等的矩形展位,每个展位的面积都为200平方米,阴影部分为宽度相等的人行通道,求人行通道的宽度.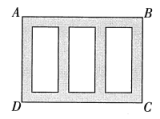 19. 习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气.”可见,阅读对学生的成长有着深远意义.为了解同学们的课外阅读情况,小明从本校七年级学生中随机抽取了10名学生,对其平均每周课外阅读时间进行了调查,统计结果如下表:
19. 习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气.”可见,阅读对学生的成长有着深远意义.为了解同学们的课外阅读情况,小明从本校七年级学生中随机抽取了10名学生,对其平均每周课外阅读时间进行了调查,统计结果如下表:学生编号
①
②
③
④
⑤
⑥
⑦
⑧
⑨
⑩
平均每周课外阅读时间(单位:)
60
90
75
40
160
90
150
160
110
150
请根据以上统计结果,解答下列问题:
(1)、抽取的10名学生平均每周课外阅读时间的中位数是 .(2)、小明在调查报告中写道:“根据统计结果,估计我校七、八、九年级1500名学生中,有一半学生平均每周课外阅读时间超过 , ”你同意小明的说法吗?请说明理由.(3)、现将平均每周课外阅读时间不低于的学生评为优秀阅读者,小明准备从上表中获得优秀阅读者中随机选取两名同学进行经验交流,请用列表或画树状图的方法求被选中的两名同学的平均每周课外阅读时间都是的概率.20. 操作与发现如图,在中, , 点D,E分别是上的点,且 .
 (1)、尺规作图:请根据下列要求完成作图,并标出相应的字母.(保留作图痕迹)
(1)、尺规作图:请根据下列要求完成作图,并标出相应的字母.(保留作图痕迹)①作线段的垂直平分线交于点F;
②在边上取一点G,使得;
③连接 .
(2)、观察与思考:线段间满足怎样的等量关系,请直接写出你发现的结论.21. 某校“综合与实践”小组来到太原文瀛公园进行参观研学,对人民革命烈士纪念碑的高度进行了实地测量.项目操作如下:如图,测角仪的高度米,他们分别在点C和点D处测得纪念碑顶端A的仰角分别为 , 且米,A,E,C,B,F,D,G在同一竖直平面内,且E,F,G在同一条水平线上,C,B,D在同一条水平线上,求纪念碑的高度.(结果精确到0.1米,) 22. 综合与实践
22. 综合与实践问题情境

如图1,在正方形中,点O是对角线上一点,且 , 将正方形绕点O按顺时针方向旋转得到正方形(点分别是点A,B,C,D的对应点).
(1)、探究发现如图2,当边与在同一条直线上,与在同一条直线上时,点与分别落在正方形的边与上.求证:四边形是矩形.
(2)、如图3,当边经过点C时,猜想线段与的数量关系,并加以证明.(3)、问题拓展如图4,在正方形绕点O按顺时针方向旋转过程中,直线与交于点P,连接 . 当点P在边的左侧时,请直接写出的度数.
23. 综合与探究如图,抛物线与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,且A,B两点的坐标分别是 . 点P是抛物线上的一个动点,点P的横坐标为m,过点P作直线轴,交直线于点G,交直线于点H.
 (1)、求抛物线的函数表达式及点C的坐标.(2)、如果点D是抛物线的顶点,点P在点C和点D之间运动时,试判断在抛物线的对称轴上是否存在一点N,使得是等腰直角三角形,若存在,请求出点N的坐标;若不存在,请说明理由.(3)、试探究在抛物线的对称轴上是否存在点Q,使得以点P,Q,B,C为顶点的四边形是平行四边形,若存在,请直接写出点P的坐标;若不存在,请说明理由.
(1)、求抛物线的函数表达式及点C的坐标.(2)、如果点D是抛物线的顶点,点P在点C和点D之间运动时,试判断在抛物线的对称轴上是否存在一点N,使得是等腰直角三角形,若存在,请求出点N的坐标;若不存在,请说明理由.(3)、试探究在抛物线的对称轴上是否存在点Q,使得以点P,Q,B,C为顶点的四边形是平行四边形,若存在,请直接写出点P的坐标;若不存在,请说明理由.