江西省上饶市玉山县2022年九年级第二次初中学业水平模拟考试数学试题

试卷更新日期：2022-05-30 类型：中考模拟

进入出卷网下载

一、单选题

1. 9的相反数是（）

A、 $- 9$ B、9 C、 $\frac{1}{9}$ D、 $- \frac{1}{9}$

查看试题解析
2. 下列几何体中，俯视图为圆的是（）

A、 B、 C、 D、

查看试题解析
3. 有10人练习射击，每人射击一次所中环数如下表：

环数/环

4

6

8

10

人数/人

3

4

2

1

则他们这次射击数据的众数与中位数分别为（）

A、4，6 B、6，6 C、4，5 D、6，5

查看试题解析
4. 已知蓄电池的电压为定值，使用蓄电池时，电流I（单位：A）与电阻R（单位： $Ω$ ）是反比例函数关系，它的图象如图所示.则这个反比例函数的解析式为（）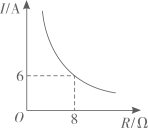

A、 $I = \frac{24}{R}$ B、 $I = \frac{36}{R}$ C、 $I = \frac{48}{R}$ D、 $I = \frac{64}{R}$

查看试题解析
5. 如图，点A、B、C在 $⊙ O$ 上， $∠ A C B = 54 °$ ，则 $∠ B A O$ 的度数是（）

A、54° B、27° C、36° D、108°

查看试题解析
6. 如图，抛物线 $y = a x^{2} + b x + c$ 的对称轴是 $x = 1$ ，下列结论：① $a b c > 0$ ；② $b^{2} - 4 a c > 0$ ；③ $3 a + c > 0$ ；④ $5 a + b + 2 c > 0$ ，正确的有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

7. 计算 $\frac{1}{2 x} - \frac{1}{3 x}$ 的结果是．

查看试题解析
8. 分解因式： $\frac{1}{4} x^{2} - 1 =$ ．

查看试题解析
9. 方程组 ${\begin{array}{l} x + 2 y = 5 \\ 2 x - y = 0 \end{array}$ 的解为．

查看试题解析
10. 2020年6月23日，中国自主研发的北斗三号最后一颗卫星成功发射．据统计，现在国内已有超过6 900 000辆营运车辆导航设施应用北斗系统，数据6 900 000用科学记数法表示为．

查看试题解析
11. 如图，直线 $A B$ ， $C D$ 相交于点 $O$ ， $O E ⊥ C D$ ，垂足为点 $O$ ．当直线 $A B$ 绕着点 $O$ 在 $∠ D O E$ 内部转动， $O F$ 是 $∠ A O C$ 的角平分线，若 $∠ B O E = α$ ，则 $∠ A O F = β$ ，则 $β$ 关于 $α$ 的函数关系式为．

查看试题解析
12. 正方形ABCD的边长是4，点P是AD边的中点，点E是正方形边上的一点．若△PBE是等腰三角形，则腰长为 .

查看试题解析

三、解答题

13.

(1)、如果单项式 $3 x^{m} y$ 与 $- 5 x^{3} y^{n}$ 是同类项，求m+n的值．

(2)、已知：如图，E是 $▱ A B C D$ 的边BC延长线上的一点，且 $C E = B C$ ．求证： $△ A B C$ ≌ $△ D C E$ ．

查看试题解析
14. 已知关于x的一元二次方程 $x^{2} - x + 2 m = 0$ 有两个不相等的实数根 $x_{1}$ ， $x_{2}$ ，且 $x_{1} x_{2} > - 1$ ，求实数m的取值范围．

查看试题解析
15. 请仅用无刻度直尺完成以下作图．（保留画图痕迹，不写作法）
已知四边形ABCD内接于 $⊙ O$ ，且已知 $∠ A D C = 120 °$ ．

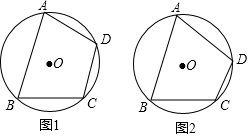(1)、在图1中已知 $A D = C D$ ，在 $⊙ O$ 上求作一个度数为30°的圆周角；

(2)、在图2中，已知 $A D \neq C D$ ，在 $⊙ O$ 上求作一个度数为30°的圆周角．

查看试题解析
16. 有4张看上去无差别的卡片，上面分别写有数-1，2，4，8．

(1)、随机抽取一张卡片，求抽取到的数是偶数的概率；

(2)、随机抽取一张卡片后，放回并混在一起，再随机抽取一张，请用画树状图或列表法，求抽取出的两数之差的绝对值大于3的概率．

查看试题解析
17. 了解同学们“智慧作业”平台使用的熟练程度，某校随机抽取了部分同学进行调查，并将调查结果绘制成如图两幅尚不完整的统计图．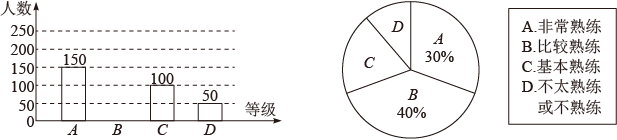
根据以上信息，回答下列问题：

(1)、本次调查的样本容量是，扇形统计图中表示A等级的扇形圆心角为°；比较熟练的同学人数人；

(2)、学校拟对“不太熟练或不熟练”的同学进行平台使用的培训，若该校有2000名学生，试估计该校需要培训的学生人数．

查看试题解析
18. 图，在直角坐标系中，直线 $y_{1} = a x + b$ 与双曲线 $y_{2} = \frac{k}{x} (k \neq 0)$ 分别相交于第二、四象限内的 $A (m ， 4)$ ， $B (6 ， n)$ 两点，与x轴相交于C点，与y轴相交于D点．已知 $O C = 3$ ， $t a n ∠ A C O = \frac{2}{3}$ ．

(1)、点C坐标是，点D坐标是；

(2)、求 $y_{1}$ ， $y_{2}$ 对应的函数表达式；

(3)、求 $△ A O B$ 的面积．

查看试题解析
19. 有一种升降熨烫台如图1所示，其原理是通过改变两根支撑杆夹角的度数来调整熨烫台的高度．图2是这种升降熨烫台的平面示意图．AB和CD是两根相同长度的活动支撑杆，点O是它们的连接点，OA=OC，h（cm）表示熨烫台的高度．

(1)、如图2﹣1．若AB=CD=110cm，∠AOC=120°，求h的值；

(2)、爱动脑筋的小明发现，当家里这种升降熨烫台的高度为120cm时，两根支撑杆的夹角∠AOC是74°（如图2﹣2）．求该熨烫台支撑杆AB的长度（结果精确到1cm）．
（参考数据：sin37°≈0.6，cos37°≈0.8，sin53°≈0.8，cos53°≈0.6．）

查看试题解析
20. 某社区拟建 $A$ ， $B$ 两类摊位以搞活“地摊经济”，每个 $A$ 类摊位的占地面积比每个 $B$ 类摊位的占地面积多2平方米，建 $A$ 类摊位每平方米的费用为40元，建 $B$ 类摊位每平方米的费用为30元，用60平方米建 $A$ 类摊位的个数恰好是用同样面积建 $B$ 类摊位个数的 $\frac{3}{5}$ ．

(1)、求每个 $A$ ， $B$ 类摊位占地面积各为多少平方米？

(2)、该社拟建 $A$ ， $B$ 两类摊位共90个，且 $B$ 类摊位的数量不少于 $A$ 类摊位数量的3倍.求建造这90个摊位的最大费用．

查看试题解析

21. 探究函数性质时，我们经历了列表、描点、连线画出函数图象，观察分析图像特征，概括函数性质的过程．结合已有的学习经验，请画出函数

y_{1} = - \frac{12}{x^{2} + 2}

的图象并探究该函数的性质．

x	…	$- 4$	$- 3$	$- 2$	$- 1$	0	1	2	3	4	…
$y_{1}$	…	$- \frac{2}{3}$	a	$- 2$	$- 4$	b	$- 4$	$- 2$	$- \frac{12}{11}$	$- \frac{2}{3}$	…
$y_{2}$				c	d	e	f	g

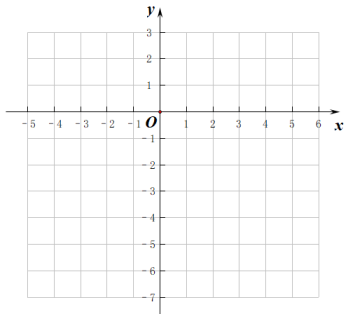(1)、列表，写出表中a，b的值：a＝ ▲ ， b＝ ▲ ；描点、连线，在所给的平面直角坐标系中画出该函数的图象．

(2)、观察函数图象，判断下列关于函数性质的结论是否正确，在下面横线上填入“序号”或填入“无”，正确的是，错误的是．

①函数 $y_{1} = - \frac{12}{x^{2} + 2}$ 的图象关于y轴对称；

②当 $x = 0$ 时，函数 $y_{1} = - \frac{12}{x^{2} + 2}$ 有最小值，最小值为 $- 6$ ；

③在自变量的取值范围内函数y的值随自变量x的增大而减小．

(3)、已知二次函数

y_{2} = x^{2} - 6

，请你写出表中c，d，e，f，g的值：c＝ ▲ ， d＝ ▲ ， e＝ ▲ ， f＝ ▲ ， g＝ ▲ ，并在所给的同一坐标系中画出函数

y_{2} = x^{2} - 6

的图像，结合你所画的函数图象，直接写出不等式

6 - \frac{12}{x^{2} + 2} < x^{2}

的解集．

查看试题解析

22. 如图1，在四边形ABCD中， $A 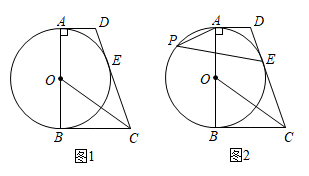D ∥ B C$ ， $∠ D A B = 90 °$ ， AB是 $⊙ O$ 的直径，CO平分 $∠ B C D$ ．

(1)、求证：直线CD与 $⊙ O$ 相切；

(2)、如图2，记（1）中的切点为E，P为优弧 $\overset{⌢}{A B E}$ 上一点， $A D = 1$ ， $B C = 2$ ．
①求 $⊙ O$ 的直径AB；
②求 $t a n ∠ A P E$ 的值．

查看试题解析
23. 【基础巩固】

(1)、如图1，在△ABC中，D为AB上一点，∠ACD＝∠B．求证：AC²＝AD•AB．

(2)、【尝试应用】
如图2，在▱ABCD中，E为BC上一点，F为CD延长线上一点，∠BFE＝∠A．若BF＝4，BE＝3，求AD的长．

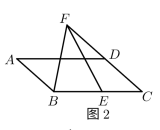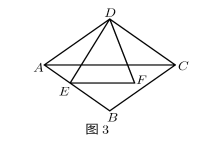
(3)、【拓展提高】
如图3，在菱形ABCD中，E是AB上一点，F是△ABC内一点，EF∥AC，AC＝2EF，∠EDF＝ $\frac{1}{2}$ ∠BAD，AE＝2，DF＝5，求菱形ABCD的边长．

查看试题解析

环数/环	4	6	8	10
人数/人	3	4	2	1