江西省吉安市吉州区2022年初中学业水平模拟考试数学试题
试卷更新日期:2022-05-30 类型:中考模拟
一、单选题
-
1. |-2022|的倒数是( )A、2022 B、 C、-2022 D、-
-
2. 下列各式中,计算结果为a8的是( )A、 B、 C、 D、
-
3. 运动会的领奖台可以近似的看成如图所示的立体图形,则它的左视图是( )
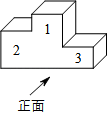 A、
A、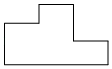 B、
B、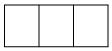 C、
C、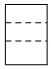 D、
D、
-
4. 北京时间2022年4月16日09时56分,神舟十三号载人飞船返回舱在东风着陆场成功着陆,代表着此次载人飞行任务取得圆满成功,神舟十三号飞船的飞行速度每小时约为28440000米,将数据28440000科学记数法表示为( )A、 B、 C、 D、
-
5. 某校开展“展青春风采,树强国信念”科普大阅读活动.小明看到黄金分割比是一种数学上的比例关系,它具有严格的比例性、艺术性、和谐性,蕴藏着丰富的美学价值,应用时一般取0.618.特别奇妙的是在正五边形中,如图所示,连接AB,AC,的角平分线交边AB于点D,则点D就是线段AB的一个黄金分割点,且 , 已知 , 那么该正五边形的周长为( )
 A、19.1cm B、25cm C、30.9cm D、40cm
A、19.1cm B、25cm C、30.9cm D、40cm -
6. 如图,对称轴为 的抛物线 与 轴的交点在1和2之间,与 轴的交点在 和0之间,则下列结论错误的是( )
 A、 B、此抛物线向下移动 个单位后过点 C、 D、方程 有实根
A、 B、此抛物线向下移动 个单位后过点 C、 D、方程 有实根
二、填空题
-
7. 命题:“64的平方根为8”是命题(填“真”或“假”).
-
8. 不等式组 的解集是 .
-
9. 实数 , 是一元二次方程 的两个根,则多项式 的值为.
-
10. 七巧板起源于我国先秦时期,古算书《周髀算经》中有关于正方形的分割术,经过历代演变而成七巧板,如图1所示.19世纪传到国外,被称为“唐图”(意为“来自中国的拼图”),图2是由边长为8的正方形分割制作的七巧板拼摆成的“叶问蹬”图.则图中抬起的“腿”(即阴影部分)的面积为 .
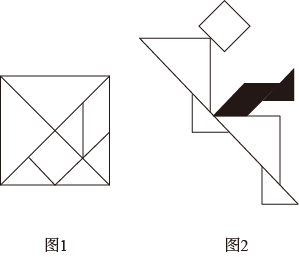
-
11. 如图,已知在矩形ABCD中,AB=1,BC= ,点P是AD边上的一个动点,连结BP , 点C关于直线BP的对称点为 ,连接C .当点P运动时,点 也随之运动.若点P从点A运动到点D , 则线段C 扫过的区域的面积是 .

-
12. 如图,在半径为1的⊙O中,直线l为⊙O的切线,点A为切点,弦AB=1,点P在直线l上运动,若△PAB为等腰三角形,则线段OP的长为 .

三、解答题
-
13.(1)、计算:(2)、如图, , , , , 求AC的长.

-
14. 先化简,再求值: , 其中x满足 .
-
15. 读高中的小明从家到学校需要中途转一趟车,从家到站台M可乘A,B,C三路车(小明乘A,B,C三路车的可能性相同)到了站台M后可以转乘D路或E路车直接到学校(小明乘D,E两路车的可能性相同).(1)、“小明从家到站台M乘坐A路车”是事件(填“不可能”或“必然”或“随机”),小明从站台M到学校乘坐F路车的概率为 .(2)、请用列表或画树状图的方法,求小明先乘坐A路车,再转乘D路或E路车到学校的概率.
-
16. 如图,在正方形ABCD中,点E、F分别在BC、CD上,且 , 请仅用无刻度的直尺分别按下列要求作图(保留作图痕迹).

 (1)、在图①中,以点E、F为顶点作正方形EGHF;(2)、在图②中,连接AE、BF交于点P,以点P为顶点作正方形.
(1)、在图①中,以点E、F为顶点作正方形EGHF;(2)、在图②中,连接AE、BF交于点P,以点P为顶点作正方形. -
17. 如图,O为坐标原点,直线l⊥y轴,垂足为M,反比例函数y= (k≠0)的图象与l交于点A(m,3),△AOM的面积为6
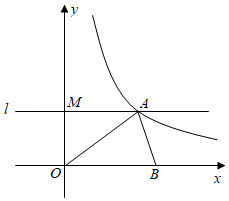 (1)、求m、k的值;(2)、在x轴正半轴上取一点B,使OB=OA,求直线AB的函数表达式.
(1)、求m、k的值;(2)、在x轴正半轴上取一点B,使OB=OA,求直线AB的函数表达式. -
18. 接种疫苗是阻断新冠病毒传播的有效途径,针对疫苗急需问题,某制药厂紧急批量生产,计划每天生产疫苗16万剂,但受某些因素影响,有10名工人不能按时到厂.为了应对疫情,回厂的工人加班生产,由原来每天工作8小时增加到10小时,每人每小时完成的工作量不变,这样每天只能生产疫苗15万剂.(1)、求该厂当前参加生产的工人有多少人?(2)、生产4天后,未到的工人同时到岗加入生产,每天生产时间仍为10小时.若上级分配给该厂共760万剂的生产任务,问该厂共需要多少天才能完成任务?
-
19. 为了落实立德树人根本任务,积极响应“双减”政策要求,某校开设了丰富的劳动教育课程.某日,学生处对学校菜圃耕作情况进行了一次评分.从七、八年级各随机抽取20块菜圃,对这部分菜圃的评分进行整理和分析(菜圃评分均为整数,满分为10分,9分(含9分)以上为“五星菜圃”).相关数据统计、整理如下:
抽取七年级菜圃的评分(单位:分):
6,6,7,6,6,7,9,7,9,7,9,9,7,9,9,10,9,9,9,10.
抽取八年级菜圃的评分(单位:分):
8,8,7,7,9,9,7,7,7,9,9,7,7,7,8,8,8,9,9,10.
[七、八年级抽取的菜圃评分统计]
年级
平均数
中位数
众数
方差
七年级
8
a
9
2.65
八年级
8
8
b
c

根据以上信息,解答下列问题:
(1)、填空:a= , b= , c= .(2)、该校七年级共20个班,每班有4块菜圃,估计该校七年级“五星菜圃”的数量;(3)、请你利用上述统计图表,对七、八年级的菜圃耕种情况写出两条合理的评价. -
20. 首钢滑雪大跳台是世界上首个永久性的单板大跳台,其优美的造型,独特的设计给全球观众留下深刻的印象,大跳台场地分为助滑区、起跳台、着陆坡和终点区域4个部分.现将大跳台抽象成右边的简图,FC表示运送运动员上跳台的自动扶梯,CD表示助滑区,表示起跳台,EB表示着陆坡.已知 , , 在助滑区D处观察到顶点C处的仰角是30°,且自动扶梯的速度是2m/s,运送运动员到达跳台顶端C点处需要30秒, , , CA、DG、EH都垂直于BF.
 (1)、求大跳台AC的高度是多少米(结果精确到0.1m);(2)、首钢滑雪大跳台主体结构采用装配式钢结构体系和预制构件,“助滑区”和“着陆坡”赛道面宽35米,面板采用10mm耐候钢,密度为 , 求铺装“助滑区”和“着陆坡”赛道的耐候钢总重量是多少吨(结果精确到1吨).( , )
(1)、求大跳台AC的高度是多少米(结果精确到0.1m);(2)、首钢滑雪大跳台主体结构采用装配式钢结构体系和预制构件,“助滑区”和“着陆坡”赛道面宽35米,面板采用10mm耐候钢,密度为 , 求铺装“助滑区”和“着陆坡”赛道的耐候钢总重量是多少吨(结果精确到1吨).( , ) -
21. 如图,AB是⊙O的直径,点C为⊙O上一点,点P是半径OB上一动点(不与O,B重合),过点P作射线l⊥AB,分别交弦BC,于D、E两点,在射线l上取点F,使FC=FD.
 (1)、求证:FC是⊙O的切线;(2)、当点E是的中点时,
(1)、求证:FC是⊙O的切线;(2)、当点E是的中点时,① 若∠BAC=60°,判断以O,B,E,C为顶点的四边形是什么特殊四边形,并说明理由;
② 若 , 且AB=20,求OP的长.
-
22. 【阅读理解】已知关于x、y的二次函数y=x-2ax+a+2a=(x-a)+2a,它的顶点坐标为(a,2a),故不论a取何值时,对应的二次函数的顶点都在直线y=2x上,我们称顶点位于同一条直线上且形状相同的抛物线为同源二次两数,该条直线为根函数.(1)、【问题解决】
若二次函数y=x+2x-3和y=-x-4x-3是同源二次函数,求它们的根函数;
(2)、已知关于x、y的二次函数C:y=x-4mx+4m-4m+1,完成下列问题:①求满足二次函数C的所有二次函数的根函数;
②若二次函数C与直线x=-3交于点P,求点P到x轴的最小距离,请求出此时m为何值?并求出点P到x轴的最小距离;
-
23. 综合与实践
数学实践活动,是一种非常有效的学习方式.通过活动可以激发我们的学习兴趣,提高动手动脑能力,拓展思推空间,丰富数学体验.让我们一起动手来折一折、转一转、剪一剪,体会活动带给我们的乐趣.
折一折:将正方形纸片ABCD折叠,使边AB、AD都落在对角线AC上,展开得折痕AE、AF , 连接EF , 如图1.
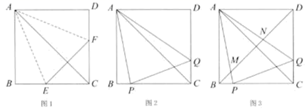 (1)、 ,写出图中两个等腰三角形:(不需要添加字母);(2)、转一转:将图1中的 绕点A旋转,使它的两边分别交边BC、CD于点P、Q , 连接PQ , 如图2.
(1)、 ,写出图中两个等腰三角形:(不需要添加字母);(2)、转一转:将图1中的 绕点A旋转,使它的两边分别交边BC、CD于点P、Q , 连接PQ , 如图2.线段BP、PQ、DQ之间的数量关系为;
(3)、连接正方形对角线BD , 若图2中的 的边AP、AQ分别交对角线BD于点M、点N . 如图3,则 ;(4)、剪一剪:将图3中的正方形纸片沿对角线BD剪开,如图4.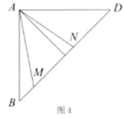
求证: .
