江西省赣州市2022年九年级学业水平适应性考试数学试题

试卷更新日期：2022-05-30 类型：中考模拟

进入出卷网下载

一、单选题

1. 化简：－（－6）的结果是（）．

A、－6 B、 $- \frac{1}{6}$ C、6 D、 $\frac{1}{6}$

查看试题解析
2. 下列2022年北京冬奥会吉祥物冰墩墩的图形中，是轴对称图形的是（）．

A、 B、 C、 D、

查看试题解析
3. 如图1，是七巧块，又叫立体七巧板，它是利用七块不相同的立体积件组成的立体图形；那么图2不可能是下列哪个积件的视图（）．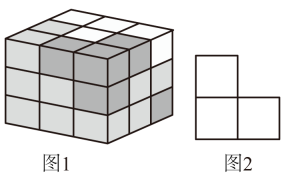

A、 B、 C、 D、

查看试题解析
4. 用一张宽为x的矩形纸片剪成四个全等的直角三角形，如图1，然后把这四个全等的直角三角形纸片拼成一个赵爽弦图；如图2，若弦图的大正方形的边长为6，中间的小正方形面积为S，请探究S与x之间是什么函数关系（）．

A、一次函数 B、二次函数 C、反比例函数 D、其它函数

查看试题解析
5. 若关于x的不等式组 ${\begin{array}{l} 2 x + 1 > 6 \\ x - a \leq 0 \end{array}$ 恰有2个整数解，则实数a的取值范围是（）．

A、 $4 < a < 5$ B、 $4 < a \leq 5$ C、 $4 \leq a \leq 5$ D、 $4 \leq a < 5$

查看试题解析
6. 用绘图软件绘制出函数 $y = \frac{a x}{(x + b)^{2}}$ 的图象，如图，则根据你学习函数图象的经验，下列对a，b大小的判断，正确的是（）．

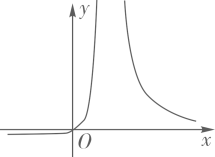A、a＞0，b＜0 B、a＞0，b＞0 C、a＜0，b＞0 D、a＜0，b＜0

查看试题解析

二、填空题

7. 因式分解： $x^{2} + 2 x y + y^{2} - 1 =$ ．

查看试题解析
8. 光年是天文学中一种计量天体时空距离的长度单位，1光年约为9500000000000千米，将数9500000000000用科学记数法表示应为．

查看试题解析
9. 已知 $α$ ， $β$ 是方程 $x^{2} - 2 x - 4 = 0$ 的两根，则 $α^{2} - α + β =$ ．

查看试题解析
10. 我国古代数学著作《孙子算经》中有“多人共车”问题：今有三人共车，二车空；二人共车，九人步．问人与车各几何？其大意是：每车坐3人，两车空出来；每车坐2人，多出9人无车坐．问人数和车数各多少？设车x辆，根据题意，可列出的方程是．

查看试题解析
11. 如图，矩形ABCD中，AB＝8cm，AD＝6cm，矩形ABCD绕它的对称中心O旋转一周，边AD扫过的面积是cm² ．

查看试题解析
12. 如图，矩形ABCD中，AB＝6，AD＝2，点E是边CD的中点，点P在AB边上运动，点F为DP的中点；当 $△ D E F$ 为等腰三角形时，则AP的长为．

查看试题解析

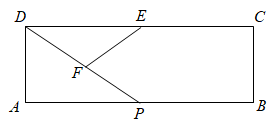
三、解答题

13.

(1)、计算： $4 c o s 30 ° + | \sqrt{3} - 4 | - {(\frac{1}{2})}^{- 2}$ ；

(2)、如图，一把直尺与一块三角板如图放置，若 $∠ 1 = 24 °$ ，求 $∠ 2$ 的度数．

查看试题解析
14. 先化简，再求值： $\frac{5}{a} + \frac{a^{2} - 4}{a - 1} \div \frac{a^{2} + 2 a}{a - 1}$ ，其中a＝3．

查看试题解析
15. 如图，点C是以AB为直径的半圆O内任意一点，连接AC，BC，点D在AC上，且AD＝CD，请仅用无刻度的直尺分别按下列要求画图（保留画图痕迹）．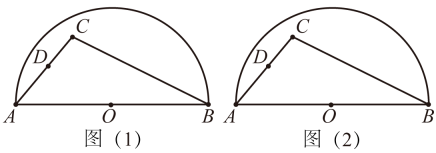

(1)、在图（1）中，画出 $△ A B C$ 的中线AE；

(2)、在图（2）中，画出 $△ A B C$ 的角平分线AF．

查看试题解析
16. 第24届北京冬奥会开幕式的“二十四节气倒计时”节目，向全世界人民展示了中华文化的魅力．为了让学生了解二十四节气，某老师将每个节气的名称写在完全相同的不透明卡片上，将卡片洗均后背面朝上置于桌面，邀请同学随机抽取一张卡片，并让该同学介绍所抽取卡片上对应节气的含义．

(1)、随机抽取一张卡片，上面写有“立春”的概率为；

(2)、若老师将“立春、雨水、春分、谷雨”四张卡片单独拿出，邀请小明和小华同学同时在其中各抽取一张．请利用画树状图或列表的方法，求两人抽到的卡片上的节气有相同的字的概率．

查看试题解析
17. 如图，菱形ABCD在第一象限，点A、B分别在y轴、x轴上，对角线 $A C ∥ x$ 轴，点 $C (12 ， 3)$ ，反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象交边AD于点P，且AP∶PD＝1∶2．

(1)、求k的值；

(2)、将菱形ABCD沿y轴向下平移m个单位，当点D落在反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象时，求菱形ABCD平移所扫过的面积．

查看试题解析
18. 习总书记说：“中国人的饭碗任何时候都要牢牢端在自己手上”，某小麦实验基地为了考察甲、乙两种小麦的长势，分别从中随机抽取10株麦苗的高度（数据均为整数，单位：cm），对这些数据进行整理、描述和分析如下：
甲种小麦的苗高（cm）：见折线统计图
乙种小麦的苗高（cm）：11，16，18，14，12，19，6，8，10，16；
甲、乙两种小麦的苗高数据统计表

平均数
中位数
众数
方差
甲
13
13.5
a
4
乙
13
b
16
16.8
根据以上图表信息，完成下列问题：

(1)、在统计图中补上乙种小麦的苗高折线统计图；

(2)、填空：a＝， b＝；

(3)、若实验基地有甲种小麦2000株，请你估计甲种小麦苗高不低于12cm的株数；

(4)、请你从某个角度对甲、乙两种小麦的长势作对比分析，并说明理由．

查看试题解析
19. 图1是某小型汽车的示意图，图2是其后备厢的箱盖打开过程侧面简化示意图，五边形ABCDE表示该车的后备厢的厢体侧面，在打开后备厢的过程中，箱盖AED可以绕点A逆时针方向旋转，当旋转角为60°时，箱盖AED落在 $A E^{'} D^{'}$ 的位置．若 $∠ E A B = ∠ A B C = ∠ B C D = 90 °$ ， $∠ A E D = 150 °$ ， AE＝80厘米，ED＝40厘米，DC＝25厘米，且后备厢底部BC离地面的高CN＝25厘米．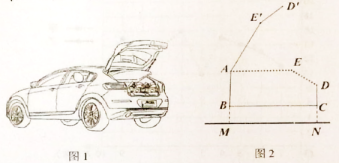

(1)、求点 $D^{'}$ 到地面MN的距离（结果保留根号）；

(2)、求箱盖打开60°时的宽D， $D^{'}$ 两点的距离（参考数据： $\sqrt{3} \approx 1.73$ ， $\sqrt{5 + 2 \sqrt{3}} \approx \sqrt{8.464} \approx 2.91$ ， $\sqrt{13536} \approx 116.3$ ，结果取整数）．

查看试题解析
20. 已知 $⊙ O$ 与正方形ABCD如图放置，点A，B在 $⊙ O$ 上．

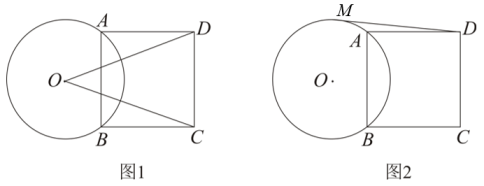(1)、如图1，连接OC，OD，求证：OC＝OD；

(2)、如图2，点M在 $⊙ O$ 上，连接DM，已知 $⊙ O$ 的半径为5， $D M = 4 \sqrt{7}$ ， AB＝8；求证：DM是 $⊙ O$ 的切线．

查看试题解析
21. 因环保节能，新能源汽车越来越受到消费者的青睐；某经销商分两次购进甲、乙两种型号的新能源汽车（两次购进同一种型号汽车每辆的进价相同）．第一次用360万元购进甲型号汽车20辆和乙型号汽车30辆；第二次用260万元购进甲型号汽车10辆和乙型号汽车35辆．

(1)、求甲、乙两种型号新能源汽车每辆的进价；

(2)、经销商分别以每辆甲型号汽车14.3万元，每辆乙型号汽车5.8万元的价格销售．
①经销商发现乙种型号新能源汽车销售较好，每月能售10台，市场调查发现售价每降低0.2万元，销售量会增加2台，问乙种型号新能源汽车定价为多少万元时，月销售乙种型号新能源汽车获取的利润最大？
②根据销售情况，经销商决定再次购进甲、乙两种型号的新能源汽车共100辆，且乙型号汽车的辆数不少于甲型号汽车辆数的2倍，若两种型号汽车每辆的进价不变，甲型号汽车的售价不变，而乙型参照①中最大利润的定价销售，请你求出获利最大的购买方案，并求出此批100辆汽车销售完的最大利润是多少．

查看试题解析
22. 在等腰三角形ABC中，AC＝BC，点P为BC边上一点（不与B、C重合），连接PA，以P为旋转中心，将线段PA顺时针旋转，旋转角与 $∠ C$ 相等，得到线段PD，连接DB．

(1)、特例感知
如图1，当 $∠ C = 90 °$ 时，求 $∠ D B A$ 的度数；

(2)、拓展探究
如图2，若 $∠ C = α$ ，求 $∠ D B A$ 的度数（用含 $α$ 的代数式表示）；

(3)、问题解决
如图3，连接AD，若 $∠ C = α$ ，且 $t a n α = \frac{5}{12}$ ， AC＝13， $∠ A P C = 135 °$ ，求AD的长．

查看试题解析
23. 如图1，在平面直角坐标系中，抛物线 $y_{0} = x^{2} + b x + c$ 与x轴交于点 $A (- 2 ， 0)$ ，点 $B (6 ， 0)$ ，与y轴交于点C．

(1)、求抛物线 $y_{0}$ 的表达式及点C的坐标；

(2)、若点 $D_{0}$ 是地物线 $y_{0}$ 上一动点，连接 $C D_{0}$ ，点 $D_{0}$ 在抛物线 $y_{0}$ 上运动时；
①取 $C D_{0}$ 的中点 $D_{1}$ ，当点 $D_{0}$ 与点A重合时， $D_{1}$ 的坐标为 ▲ ；当点 $D_{0}$ 与点B重合时， $D_{1}$ 的坐标为 ▲ ；请在图2的网格中画出点 $D_{1}$ 的运动轨迹，并猜想点 $D_{1}$ 的运动轨迹是什么图形： ▲ ；并求点 $D_{1}$ 运动轨迹的函数 $y_{1}$ 的解析式；
②在线段 $C D_{1}$ 上取中点 $D_{2}$ ，点 $D_{2}$ 运动轨迹的函数的解析式为 $y_{2}$ ，在线段 $C D_{2}$ 上取中点 $D_{3}$ ，点 $D_{3}$ 的运动轨迹的函数的解析式为 $y_{3}$ ， …，在线段 $C D_{n - 1}$ 上取中点 $D_{n}$ ，点 $D_{n}$ 的运动轨迹的函数的解析式为 $y_{n}$ （n为正整数）；请求出函数 $y_{n}$ 的解析式（用含n的式子表示）．
③若直线y＝x＋m与系列函数 $y_{0}$ ， $y_{1}$ ， $y_{2}$ ， …， $y_{n}$ 的图象共只有4个交点，求m的取值范围．

查看试题解析

	平均数	中位数	众数	方差
甲	13	13.5	a	4
乙	13	b	16	16.8