（人教版）2021-2022学年度第二学期八年级数学第20章数据的分析 期末复习测试卷
试卷更新日期：2022-05-27 类型：复习试卷
一、单选题
-
1. 小明参加校园歌手比赛，唱功得85分，音乐常识得95分，综合知识得90分，学校如果按如图所示的权重计算总评成绩，那么小明的总评成绩是（ ）
A、87分 B、87.5分 C、88.5分 D、89分2. 某手表厂抽查了10只手表的日走时误差，数据如下表所示：日走时误差（单位：s）
0
1
2
3
只数（单位：只）
3
4
2
1
则这10只手表的平均日走时误差（单位：s）是（ ）
A、0 B、0.6 C、0.8 D、1.13. 某校为了解学生睡眠情况，随机调查部分学生一周平均每天的睡眠时间，结果如下表：时间/小时
7
8
9
10
人数
6
9
11
4
这些学生睡眠时间的众数、中位数是（ ）
A、众数是11，中位数是8.5 B、众数是10，中位数是5 C、众数是9，中位数是9 D、众数是9，中位数是8.54. 数列5，3，4，6，8，7的中位数是（ ）A、4 B、6 C、5.5 D、55. 在对一组样本数据进行分析时，小明列出了方差的计算公式： ，由公式提供的信息，判断下列关于样本的说法错误的是（ ）A、平均数是8 B、众数是6 C、中位数是9 D、方差是3.66. 有一组数据为 ， ， ， ，这组数据的每一个数都减去 后得一组新的数据 ， ， ， ，这两组数据一定不变的是（ ）A、中位数 B、众数 C、平均数 D、方差7. 甲、乙、丙、丁四名学生近4次数学测验成绩的平均数都是105分，方差分别是 ， ， ， 则这四名学生的数学成绩最稳定的是（ ）A、甲 B、乙 C、丙 D、丁8. 5月1日至7日，我市每日最高气温如图所示，则下列说法不正确的是（ ）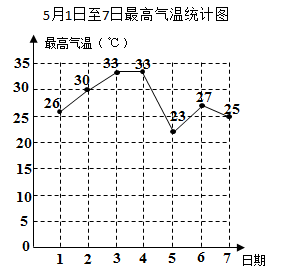
A、中位数是 B、众数是 C、平均数是 D、4日至5日最高气温下降幅度较大9. 为了向建党一百周年献礼，我市中小学生开展了“红色经典故事”主题演讲比赛。某参赛小组6名同学的成绩（单位：分）分别为：85，82，86，82，83，92.关于这组数据，下列说法错误的是（ ）A、众数是82 B、中位数是84 C、方差是84 D、平均数是8510. 学校为了丰富学生课余活动，开展了一次“爱我中华，唱我中华”的歌咏比赛，共有18名同学人围，他们的决赛成绩如下表：成绩（分）
9.40
9.50
9.60
9.70
9.80
9.90
人数
2
3
5
4
3
1
则入围同学决赛成绩的中位数和众数分别是（ ）
A、9.70分，9.60分 B、9.60分，9.60分 C、9.60分，9.70分 D、9.65分，9.60分二、填空题
-
11. 某同学5次数学小测验的成绩分别为95分，85分，95分，90分，85分，则该同学这5次成绩的平均数是分．12. 已知一组数据2，2，8，x，7，4的中位数为5，则x的值是 ．13. 下表记录了甲、乙、丙三名射击运动员最近几次选拔赛成绩的平均数和方差：
甲
乙
丙
平均数
9.35
9.35
9.34
方差
6.6
6.9
6.7
根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应选择 ．
14. 现有甲、乙两支排球队，每支球队队员身高的平均数均为1.82米，方差分别为=3.7，=4.2，则身高较整齐的球队是队．
15. 若干名同学制作卡通图片，他们制作的卡通图片张数的条形统计图如图所示，设他们制作的卡通图片张数的平均数为a，中位数为b，众数为c，则a，b，c的大小关系为。
三、解答题
-
16. 小敏参加学校举办的“我的冬奥梦"主题演讲比赛，她的演讲稿、语言表达、形象风度得分分别为86分，80分，85分，若依次按照50%，30%，20%的百分比确定最终成绩，则她的最终成绩是多少分？17. 某商场招聘员工一名，现有甲、乙、丙三人竞聘．通过计算机、语言和商品知识三项测试，他们各自成绩（百分制）如下表所示．
应试者
计算机
语言
商品知识
甲
乙
丙
若商场需要招聘负责将商品拆装上架的人员，计算机、语言和商品知识成绩分别占20%，30%，50%，计算三名应试者的平均成绩．从成绩看，应该录取谁？
18. 农科院为了解某种小麦的长势，从中随机抽取了部分麦苗，对苗高（单位： ）进行了测量．根据统计的结果，绘制出如下的统计图①和图②．
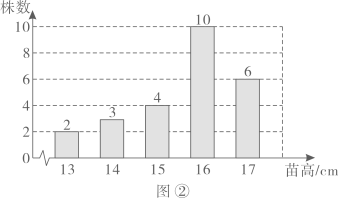
请根据相关信息，解答下列问题：
(1)、本次抽取的麦苗的株数为 ， 图①中m的值为；(2)、求统计的这组苗高数据的平均数、众数和中位数．19. 某养鸡场有2500只鸡准备对外出售.从中随机抽取了一部分鸡，根据它们的质量（单位： ），绘制出如下的统计图①和图②.请根据相关信息，解答下列问题：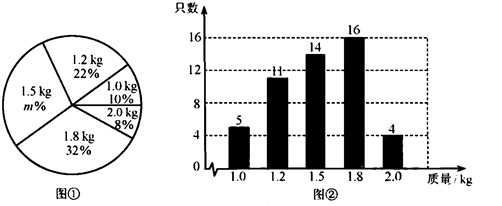
（Ⅰ）求图①中m的值；
（Ⅱ）求统计的这组数据的平均数、众数和中位数；
（Ⅲ） 根据样本数据，估计这2500只鸡中，质量为2.0kg的约有多少只？
20. 为了比较甲、乙两种水稻秧苗是否出苗整齐，每种秧苗各取5株并量出每株的高度（单位：），如下表所示：甲
12
13
15
15
10
乙
13
14
16
12
10
通过计算平均数和方差，评价哪个品种出苗整齐.
21. 某学校八、九两个年级各有学生180人，为了解这两个年级学生的体质健康情况，进行了抽样调查，过程如下，请补充完整.收集数据
从八、九两个年级各随机抽取20名学生，进行了体质健康测试，测试成绩（百分制）如下：
八年级
78
86
74
81
75
76
87
70
75
90
75
79
81
70
74
80
86
69
83
77
九年级
93
73
88
81
72
81
94
83
77
83
80
81
70
81
73
78
82
80
70
40
整理、描述数据
按如下分数段整理、描述 这两组样本数据：
成绩
人数x
部门
40≤x≤49
50≤x≤59
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤100
八年级
0
0
1
11
1
九年级
1
0
0
7
（说明：成绩80分及以上为体质健康优秀，70～79分为体质健康良好，60～69分为体质健康合格，60分以下为体质健康不合格）
分析数据
两组样本数据的平均数、中位数、众数、方差如下表所示：
年级
平均数
中位数
众数
方差
八年级
78.3
77.5
75
33.6
九年级
78
80.5
52.1
(1)、请将以上两个表格补充完整；(2)、得出结论
估计九年级体质健康优秀的学生人数为；(3)、可以推断出年级学生的体质健康情况更好一些，理由为.（至少从两个不同的角度说明推断的合理性）.22. 某校八年级（1）班同学在积极倡导和实践“低碳生活”活动中，通过调查随机抽取某城市30天的空气状况并绘制成如下统计表：空气污染指数（W）
40
60
90
110
120
天数（t）
3
3
9
10
5
其中W≤50时，空气质量为优；50＜W≤100时空气质量为良；100＜W≤150时，空气质量为轻微污染．
（1）求这个样本中空气污染指数的众数和中位数；
（2）在这个样本中空气质量为优或良的共有几天？若一年以366天计算该城市空气质量为优或良的估计约为多少天？
23. 某一企业集团有15个分公司，他们所创的利润如下表所示：公司数
1
1
2
4
2
2
3
分公司年利润（百万元）
6
1.9
2.5
2.1
1.4
1.6
1.2
（1）每个分公司所创利润的平均数是多少？
（2）该集团公司各分公司所创年利润的中位数是多少？
（3）在平均数和中位数中，你认为应该用哪一个来描述该集团公司每个分公司所创年利润的一般水平？为什么？